И 1000: НОД и НОК для 1000 и 1000 (с решением)
Кожный антисептик Скиния, 100 и 1000 мл
Позвоните нам: +7 950 477-20-80
Напишите нам: [email protected]
NailBar /Товары/Вспомогательные жидкости и препараты/Кожный антисептик Скиния, 100 и 1000 мл
Кожный антисептик Скиния — это уникальное средство на основе пропиловых спиртов которое имеет смягчающее и регенерирующее свойства.
Обьем — 100 и 1000 мл
Класс опасности — 4
Срок годности — 5 лет
Производитель — Бозон
Страна производитель — Россия
Этого товара нет в наличии, заказ недоступен.
Артикул: Н/Д Категории: Вспомогательные жидкости и препараты, Стерилизация и дезинфекция Метки: Антисептик, Бозон, Дезинфицирующее средство, Скиния
- Описание
- Отзывы (0)
Кожный антисептик Скиния, 100 и 1000 мл
Кожный антисептик Скиния — это уникальное средство на основе пропиловых спиртов которое имеет смягчающее и регенерирующее свойства.
Он обладает полным спектром бактерицидной, включая туберкулез (испытано на Mycobacterium terrae), и вирулицидной активности, включая возбудителей энтеральных и парентеральных гепатитов В и С, энтеровирусов, ротавирусов, вирусов гриппа, полиомиелита, свиного гриппа, птичьего гриппа, ВИЧ и др., фунгицидным действием в отношении грибов рода Кандида и Трихофитон, а также пролонгированным действием не менее 3 часов.действие.
Предназначен для обработки:
— Рук хирургов (2 раза по 5 мл за 5 минут).
— Инъекционного поля (за 20 секунд).
— Локтевых сгибов доноров.
— Кожи перед введением катетеров и пункций суставов.
— Гигиенической обработки рук медицинского персонала.
— При многократных обработках антисептик способствует сохранению естественного состояния кожи.
Действующие вещества:
— изо-пропиловый и нормальный пропиловый спирты (суммарно 65% об.) высокой степени очистки от ведущих мировых производителей, в результате чего антисептик не имеет резкого запаха
— синергетическая смесь алкилдиметилбензиламмоний хлорида и дидецилдиметиламмоний хлорида (суммарно 0,2%).
В состав антисептика входит уникальный по воздействию на кожу полигликозид, который:
— активирует скорость роста клеток
— защищает клетки кожи от воздействия агрессивных сред
— приводит к уменьшению воспалительной реакции без повреждения клеток
По параметрам токсичности относится к 4 классу мало опасных веществ при нанесении на кожу, введении в желудок и ингаляционном воздействии. Содержит природный полимер для уменьшения всасывания комплекса четвертичных аммониевых соединений через кожу. При многократных обработках антисептик не препятствует сохранению естественного состояния кожи.
Инструкция по применению средства
Читать онлайн «Большая дидактика и 1000 мелочей в разноуровневом обучении», Елена Яновицкая – ЛитРес
© Яновицкая Е.В., Адамский М.Я., 2005
© Русаков А.С. (подготовка текста, составление), 2005
© АНО «Агентство образовательного сотрудничества», 2005
Предисловие
В этом небольшом сборнике кратко очерчены те основные дидактические идеи, которым посвящена фундаментальная книга с дерзким и весёлым названием: «Большая дидактика и тысяча мелочей».
Её авторами, Е.В. Яновицкой и М.Я. Адамским, представлена система «разноуровневого подхода к обучению», сложившаяся в общих чертах уже в пятидесятые годы, но обстоятельно описанная лишь сорок лет спустя. «Разноуровневость» отыскивается как в способностях детей, обучающихся одновременно, так и в научной сложности изучаемых вопросов. Коллективные условия обучения совсем разных детей, очень по-разному способных осваивать тот или иной учебный предмет, зачастую называют главной трудностью в школьном деле. Здесь же в этой главной трудности видят важнейшее достоинство.
Деление типов уроков (и, соответственно, типов учебного материала) на пять уровней, выбор для каждого из них особых методов работы, принцип добровольности домашних заданий, принцип параллельной работы нескольких команд у доски, поддержка и организация взаимопомощи учеников – ряд этих (и им подобных) крупных дидактических идей и тысяча мелких нюансов педагогической работы складываются здесь в образ той живой целостности организации учебной жизни, которая предоставляет каждому ученику чувство успешности, позволяет освоить необходимое, и может послужить (а во многих школах и классах уже давно служит) основой сотрудничества взрослых и детей.
Перед нами – дело жизни Елены Васильевны Яновицкой – педагога-исследователя и организатора школьного дела «с восемьюдесятью годами педагогического стажа» (как представлялась она в конце жизни полушутя-полувсерьёз).
С 1977 года началась её совместная работа с учителем истории Михаилом Яковлевичем Адамским – человеком, год за годом старавшимся облечь систему, возникшую в живой педагогической работе, в обстоятельное описание, доступное многим, в ту книгу, которая была завершена лишь несколько лет назад. В 1986 году его статья в журнале «Профессиональное и техническое образование» стала первой публикацией об этой «новой-старой» системе, а в начале 1990-х годов в качестве заместителя руководителя роно по научно-методической работе он несколько лет координировал эксперимент с участием десятков учителей в большом числе школ Ленинского района Петербурга.
В 2000 году «Большая дидактика и тысяча мелочей» вышла первым крохотным тиражом[1]. Потом многие группы учителей в России перепечатывали и переиздавали по частям многие её фрагменты.
Мы надеемся, что вскоре эта долгожданная книга, наконец, была переиздана значительным тиражом.
А а этой книге представлено как бы сжатое её изложение – связь важнейших дидактических идей и жизненного опыта, которые позволили состояться этой системе, а её последователям – достигать удивительных результатов в своём деле.
Андрей Русаков
Глава 1. Великая дидактика без домашних заданий. Но в окружении тысячи спасительных мелочей
Основа обучения – не повторение. Основа обучения – помощь
Первый гул недоумения
Я пришла в школу ещё до войны, с матмеха университета в качестве преподавателя физики и математики. (А в 1948 году я дополнительно за год закончила пединститут и получила ещё диплом преподавателя педагогики, психологии и логики).
В сороковые годы и определились основы этой системы. До войны в школе было много проблем – но как-то не настолько остро они вставали. Жесткие формы требовательности как-то срабатывали тогда, необходимость перемен в образовании ещё не ощущалась так сильно.
А вот во время войны и особенно после – потребность в изменениях стала чувствоваться чрезвычайно. Об этом много можно рассказывать удивительных и парадоксальных историй…
К началу пятидесятых годов моя система уже в основном выстроилась, хотя и не была так чётко сформулирована как сейчас – нынешние схемы и модели отшлифовались уже к девяностым годам, названия только утрясались, даже не обо всех нужных уровнях учебной работы возникли ясные представления.
Но уже было видно, как складывающаяся система работы позволяла любому учителю совершенно менять и свои представления о детских возможностях, и учебные результаты ребят. В 1953 году я впервые представила свою систему, выступив в Ленинградском институте усовершенствования учителей с докладом, который так и назывался: «В классе сорок человек» – тогда меньше сорока и не было. И смысл заключался в том, что система, по которой я работаю, позволяет всех научить, никого не ущемляя, никого не оставляя отстающим и никого не тормозя – ни в развитии, ни в творчестве.
Что было понятно уже тогда? Что эта система позволяет учителю работать с коллективом, но так, чтобы каждому в коллективе учиться хотелось, – и чтобы каждый проучился успешно. И при этом сам процесс «способствует дальнейшему успеху через сам успех».
В школьном деле важны ведь не только цели обучения. Есть иные, не менее существенные цели, можно назвать их «целями защиты личности». Вот взгляните, что подчеркнуто нами среди их списка:
• Чтобы слабому не озвереть от неудач, не пресмыкаться и не кусаться – и суметь перейти в разряд успевающих.
• Чтобы сильному не унижать, а поднимать до себя; развивать благородство без самоуничижения; не скучать и не страдать от непонимания; любить жизнь, иметь время на увлечения и работать творчески.
• Чтобы среднему получить прочные знания о себе, о людях, о природе; понять свои сильные стороны и иметь хобби; не обижать слабого, но и не опускаться до него, не презирать сильного, а учиться у него.
• И чтобы самому учителю не потерять уважение к себе.
Из опыта многих десятилетий, многих школ, детей и взрослых я убеждалась, что эти цели достижимы относительно любых встречаемых мной детей и учителей.
Тогда же, в 1953 году, главное, что вызвало в зале гул недоумения – это отказ от обязательности домашних заданий. Но в этом отказе – первый краеугольный принцип нашей системы – школьную обязательную программу выучить на уроках (это 5–6 часов в день!), а остальное время – на лично выбранное дополнительное образование.
Обличение вместо обучения
За прошедшие десятилетия многократного опытного воплощения нашего подхода разными людьми, я убедилась, что перевод домашних заданий на исключительно добровольную основу всегда возможен (да по-своему и необходим). Когда я работала завучем, директором, я сама заменяла многие уроки. Эта система однозначно работает на любом предмете, на любом возрасте вплоть до вуза.
Но почему заявления об отмене обязательности домашних заданий так пугают учителей?
Видимо, эта обязательность необходима сегодняшней школе в качестве главного оправдания той усредненной системы работы, где учитель на уроке не учит – он что-то вещает, что-то преподает и что-то контролирует (и не свою работу, а только учащихся).
Коменский несколько столетий назад заявил о возможности учить всех. Но Коменский все-таки лишь заложил начало, показал образ возможного успеха. Вероятно, сам он и умел его достигать, но по его разработкам этого сделать невозможно. Он не обсуждал ту самую тысячу мелочей, без которых великая дидактика может быть прогрессивной только в своей формальной части – классно-урочной, где обеспечивает «массовость», стандартизацию, алгоритмизированность – учить «всех одному и тому же», а в содержательной (научить и воспитать разнообразных «всех») – остаётся лишь красивой утопией.
Педагогическая наука сделала вид, что здесь дело якобы решенное, почти само собой разумеющееся. Если не получается, то виноват или учитель, или ученик. И поскольку реального инструмента, позволяющего успешно обучать всех, учителю наука так и не предложила, то единственным оправданием его неудач стала «нерадивость» учеников. А незаменимым механизмом обличения этой нерадивости – домашние задания. Тогда всю дидактику стало возможным сводить к требовательности.
И когда недочеты дидактики не сглаживаются талантами педагога, то средний учитель стал лишь «подавать предмет» и контролировать домашнюю работу. А ученик перестал учиться на уроке – все равно дома сидеть. Домашние задания растянули время учебы почти до 10 часов в сутки. При этом труд дома не мог быть для большинства детей рациональным. Программа «преподавания» (это же не обучение!) стала безгранично возрастать. Положение попытались исправить, вменив учителю в обязанность проводить ещё дополнительные занятия с «отстающими», и слабые, уже утомленные дети сидели после уроков без обеда ещё 2–3 часа.
Роль коллектива соучеников стали рассматривать только с отрицательных позиций. Пошли на механическое разделение – «по способностям». В результате такой дискриминации учеников (а «дискриминация» по латыни и означает разделение, отделение) получили повсеместный рост молодежного экстремизма. Дети из-за безнадежности пребывания на уроках, плохого состояния знаний, из-за ухудшения здоровья наживали комплексы неполноценности, их, ничем не защищенных от криминальной среды, вынуждали и вынуждают «искать себя» на улице.
Главное уравнение дидактики: законы логики + законы этики = успех всех
Педагоги любят повторять (особенно по поводу домашних заданий): «Повторение – мать учения». Но ведь это неправда. Основа обучения не повторение само по себе, основа обучения – помощь. Вот вы, мужчина, хотите научиться вязать. Что, вы ждете, что я вас буду ругать? Нет, вы ждете, чтобы я помогла, рукой вашей поводила, подсказывала на каждом движении, принимала бы как должное все ваши повторяющиеся, неизбежные, естественные ошибки…
Помощь – основа обучения. Помощь от учителя, от соучеников, от учебника, от пособий всяких, от шпаргалок. Все интуитивно ищут такой помощи, но мало кто находит её на уроке. Но только чувство окруженности подобной помощью, возможность получить её своевременно позволяет чувствовать себя спокойно, двигаться вперёд уверенно, без боязни как отстать, так и не в меру соригинальничать.
До сих пор в педагогических кругах дидактику толкуют только как теорию «обучения», а не «воспитывающего обучения», хотя оно – воспитание – было заложено уже в использованное Я.
А. Коменским название: греческое «дидактикос» – поучительный. Уроки всегда являются «воспитывающими» сами по себе, только вопрос: что на них воспитывается. И уж конечно, люди воспитываются не программами «семейного», «полового», «правового», «экологического» и тому подобного воспитания. Люди воспитываются отношениями. Теми, что складываются вокруг них, между ними, между людьми и их делом во время жизни: работы, учебы, игры, отдыха…
Для успешной дидактики самое главное – это соединить законы логики и законы этики коллектива.
Если это удается, то учить всех сразу оказывается легче, быстрее и результативнее, чем каждого в отдельности! Тогда возникает великий шанс суметь использовать силы каждого как дар для других.
Предлагаемая нами теория «Большой дидактики и тысячи мелочей» отвечает на три главных практических вопроса:
• как обучать прямо на уроках, без «упора» на домашние задания;
• как обеспечить воспитание, влияя на него характером обучения;
• и как, обучая всех сразу, использовать многообразие этих «всех» через феномен коллектива, чтобы научить и воспитать каждого в отдельности.
Школьная доска как спортивная площадка
Дома – только хобби
Итак, домашнее задание у нас – лишь указание на ту работу, которой если хочешь, то можешь дома заняться. Оно превращено в хобби: «Ты, если хочешь, подготовься дома к тому, с чем встретишься завтра – хоть сам, хоть с папой, хоть с товарищем». А вот на уроке я предлагаю пять-семь минут, чтобы сделать на доске то, что было предложено дома посмотреть.
Можно не смотреть дома – и импровизировать на уроке на незнакомом задании. Можно дома просто взглянуть – понять, как решается, вовсе не стараясь оформить запись. А если тебе трудно – то можешь поупражняться. Ты будешь знать, что я не посмотрю в тетрадку, что там и как написано. Но зато, поработав дома, у тебя появляется уверенность в том, что будешь хорошо выглядеть на уроке. В этой системе нет таких уроков, на которых ученика не заметят.
Эстафета минутных испытаний
И вот, например, урок начинается с того, что прокручивается та задача, которая добровольно была задана.
Сделал, не сделал, не важно.
Домашнее задание – это ведь фикция, если оно обязательное. Ну, все созвонятся, спишут друг у друга. Нормально. Что тут проверять? Я буду время терять, дети будут время терять. И всё будет совершенно необъективно.
А тут все сразу видно. Все успевают «прокрутиться» с этим заданием – или у доски, или с места. Больше, чем минуту, тратить на решение задачи (если ты знаешь, как её решать) нет смысла. Представляете, сколько можно за шестьдесят секунд сделать!
И вот шесть человек – на минуту, следующие шесть – ещё на минуту – и за пять минут тридцать человек у доски побывали. И показали, кто что умеет. Не успел за минуту – значит, не успел, уступи место следующему, посмотри, в чём ты затруднялся.
Те, кто слышат об этом, восклицают: «Будут списывать, будут смотреть друг на друга!»
Во-первых, это нелегко. Посмотреть сбоку на доску трудно, к тому же психологически стыдно. Во-вторых, в твоем распоряжении всего-то минута! А в-третьих – если и посмотрят, то очень хорошо.
Не посмотрел в тетрадь, не посмотрел дома – а тут посмотрел и, может быть, понял.
Этот способ однозначно позитивен. За пять минут весь класс проверен, как он закрепил пройденный материал – и на что дальше надо будет акцентировать свое и их внимание.
Интерес к уроку: инструменты убийства и методы воскрешения
Как это выглядит? Вот три ряда, по два человека за партой. Все сидящие в ряду – р-раз, к доске на одно и то же задание. Ведь наша задача – организовать дело так, чтобы каждая минута урока так или иначе вовлекала в работу каждого ученика, чтобы минуты не пропадали даром ни для кого.
В обычной школьной ситуации у доски чаще всего один отдувается «за всех» – просто получает свою оценку. Это наихудший вариант. Время его работы – потеряно для остальных. Происходит психологическое отключение всего коллектива учеников.
Если два человека работают у доски над разными заданиями – это тоже никого не заинтересует. Только учителю чуть-чуть удобнее – быстрее.
Вот если двое у доски работают с одинаковым заданием – то уже невольно возникает сравнение, уже класс неравнодушен, даже самые озорники.
Ребята же, и стоят-то у доски по-разному, пытаются сделать по-разному, по-разному могут успеть – ведь время ограничено.
Усиливается неравнодушие «зрителей», сменяется любопытством, если у доски работают не случайные индивиды, а представители команд – а дальше будут выступать другие представители. Уже и те, кто не у доски тоже соучаствуют (по крайней мере, как болельщики).
Если же каждый ученик – участник той или иной команды, то возникающий азарт резко повышает эмоциональный уровень восприятия, устраняет безразличие, снимает усталость, подталкивает к тому, чтобы задуматься над сутью проблемы.
Перевод любопытства в любознательность
Итак, для начала нам потребуется пошагово равномерный ритм превратить в эстафету – и изменить статус выступающего у доски: от сугубо личного до делегата от команды. Для перевода случайного любопытства в направленную любознательность потребуется ввести четкий регламент, описание правил: на время, на форму, на качество, на принципы оценивания.
А число одновременно действующих у доски участников надо доводить до реально обозримого максимума – четырех-шести человек, увязать с числом команд, можно всю переднюю стену использовать, и вызывать по 10–12 человек.
На этой основе постепенно можно двигаться к решению следующей задачи – переводя любопытство в любознательность, продвигаться от спортивного интереса к познавательному. И помнить, что дети – растущий, развивающийся, меняющийся организм, и происходящее на уроках влияет на этот процесс развития, или искажая, или усиливая его.
С кого начинать?
Команды должны комплектоваться так, чтобы в каждой были ребята от самых сильных до самых слабых. А вот с кого начинать эстафету?
Когда хотят закрепить пройденное, кого обычно вызывают? Иногда случайного – кто руку тянет, или отметок мало. А чаще всего (особенно, если хотят закрепить материал) – сильного. В первом случае пользы для класса маловато, а времени может быть потеряно много, во втором – и вовсе бесполезно; кому интересно отличника слушать? Сильному потом ещё лишний раз наподдадут, как любимчику.
Тут столько ещё всяких антипедагогических нюансов возникает…
А вот кто соберет внимание всех? Только самый слабый, тот, от кого никто не ожидает толкового ответа.
И вот на первое задание выходят самые слабые. Никто из них полностью верно не справился, а время прошло. Садитесь. Или постойте. Но никому и не обидно – от них решения ещё никто и не ждал, нормально. Следующий выходит посильнее – поправит что-то, следующий ещё посильнее…
В результате за несколько минут все побывали у доски и все поработали. И если какое-то задание оказалось очень трудным – то следующее повторяется – и самый слабый начинает кувыркаться не так безнадёжно, уже выбирается сам, не прячась за товарищей.
Поскольку все это требует короткого времени, то за три-четыре таких прогона некоторый успех достигается каждым. Тут требуется учительское искусство; вы составляете задания определённого порядка, шаги короткие, маленькие задания становятся очень ясными. Скиннер, американский психолог, описал такую логику, назвал её «алгоритмом действия».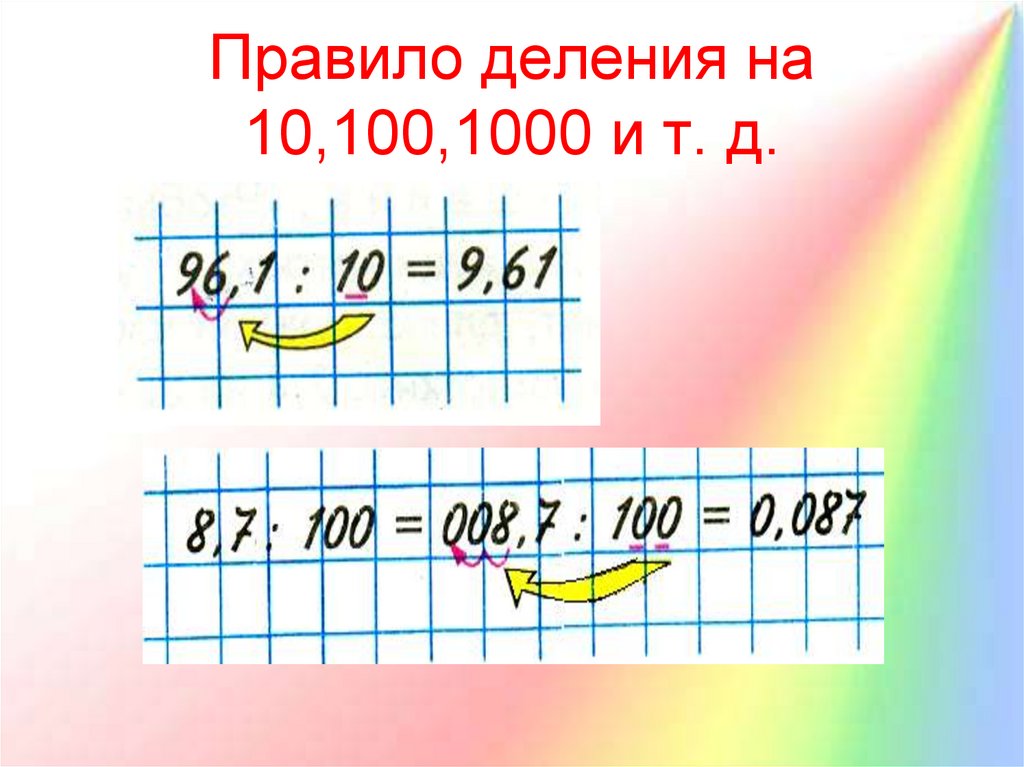
(Хотя я разработала эту логику независимо от него и значительно раньше, называя её «методом темпа».)
Так коллективно можно действовать и у доски, и у карты, и у прибора.
Устные каверзы
Можно использовать устный вариант цепочки. Задается вопрос. Время для ответа – секунд десять (два-три слова в секунду – нормальный ритм речи; если задание чёткое – то за десять секунд каждый может что-то ответить). Для устных вопросов есть свои критерии качества: если на него с ходу ответит слабый – этот вопрос не годится. Если нормальный вопрос – то задумывается сильный. (Вопрос завышен в том случае, если на него никто, кроме учителя, не ответит).
Но поскольку и сильный над вопросом задумается – то вызывать всё-таки надо слабого. Хотя мы заранее знаем, что и сильному трудно. Так почему же слабого?
Очень слабый сперва или промолчит, или ляпнет такое, что расхохочется весь класс. Да и хорошо! В школе почему-то ужасно боятся глупых или смешных ответов. А что в них плохого? (Больше всего теряется в таких случаях не ученик, а учитель: он ждал хорошего ответа, он уже подготовился с умным видом его оценить – а тут такой ляп.
) Смешная глупость всегда запоминается, все заметят различие ошибочного и верного хода мысли. Да и сам по себе быстрый и бурный общий смех во время напряженной работы, если умело делать его не обидным, – лучшая эмоциональная «подзарядка».
Мы говорим: провоцируйте плохой ответ, будьте к нему готовы. Но, совершая такую провокацию, дайте потом отвечавшему шанс, других учеников послушав, исправиться. Ведь следующий ляпнет получше, уже рядом с темой, потом кто-то скажет уже почти правильно, потом хороший ученик уже совершенно правильно ответит, а отличник (ну надо же ему как-то показать себя, не повторять же просто правильное решение) постарается выдать ещё оригинальный ответ или хотя бы выразить особое отношение к смыслу высказываний.
Увеличение количества работающих у доски соответствует потребностям коллективного обучения и, с одной стороны, повышает эффективность обучения, а с другой – решает некоторые нравственные проблемы взаимоотношений коллектива и личности.
Порядок работы «от слабого к сильному» позволяет каждому ученику реализовать самого себя и не ущемлять ничьи интересы.
Следующий вызванный увеличивает вклад в копилку знаний всего коллектива и его отдельных членов.
Критерии качества. Оценка ответов по цепочке
Есть свои тонкости и в способах составления команд, и в работе с командами, и в оценивании их. Оценивать такие «учебные эстафеты» можно разными способами. Скажем, можно суммировать результаты каждого, а оценки выставлять, например, по таким критериям:
• Единица – молчание или глупость, но думать-работать начал.
• Двойка – глупый ответ или смешной, уже что-то сделал.
• Тройка – смешной или примитивный, но удовлетворительный.
• Четвёрка – правильный, хотя и неоригинальный, хорошо.
• Пятёрка – точный, с личным отношением, не стандартный, отлично.
Каждый показал, на что способен. Но никто из вызванных не сажается на место с обвинением: «Ляпнул, плохо, садись, два!» Ни в коем случае! Школьная оценка становится не индивидуальным клеймом, а баллом, который ты приносишь своей команде. И один-два балла – это тоже что-то, чем ты смог команде помочь.
Работа идет в цепочке от слабого к сильному – и обратно. Причем повтор по цепочке обязателен! Естественно, ограничен во времени!
Такая последовательность создает комфорт для ученика. «А вот как ты ответишь теперь?» Ты выслушал все ответы, что-то заметил, запомнил, понял. Попробуй ещё раз! (Ты же перед этим «ответил» – и теперь можешь несколько минут смотреть на свою задачу со стороны).
Вот некоторые наши советы ученику:
– Отойди подальше и сядь.
– Посмотри, послушай, попробуй.
– Сравни.
– Выслушай другие мнения.
– Оцени себя.
– Приготовься ко второй попытке.
– Исправь.
– Уложись в регламент.
– За тобой остается право на несколько попыток.
Почему не возникает обиды?
Поскольку времени дается очень мало, ритм веселый, необидный. Именно веселый, не жесткий. Не получилось? Ну и что. Попробуй ещё раз, ещё раз. Поскольку все происходит весело, тебя со всех сторон поддерживают – так с чего обижаться?
Prime Numbers between 1 and 1,000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | ||||||||||
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | . | 97 | 101 | 103 | 107 | 109 | ||||
| 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | |||||||||
| 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | |||||||||
| 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | |||||||||
| 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | |||||||||
| 349 | 353 | 359 | 367 | 373 | 379 | 383 | 379 | 383 | 9000389 | 397 | 401 | |||||||
| 409 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | |||||||||
| 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | |||||||||
| 541 | 547 | 557 | 547 | 557 | 547 | 557 | 0005 563 | 569 | 571 | 577 | 587 | 593 | 599 | |||||
| 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | |||||||||
| 659 | 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 709 | 719 | 9000 727 79 9000 | ||||||
| 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | |||||||||
| 809 | 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | |||||||||
| 863 | 877 | 881 | 883 | 887 | 883 | 887 | 883 | 887 | 900007 | 911 | 919 | 929 | 937 | |||||
| 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
| Префиксы и кратные числа | Числа и формулы | Самое большое известное в мире простое число |
Источники +
Наши общие источники
- Пробеги по дорогам между городами США
Это полный урок с видео и упражнениями, показывающими, прежде всего, общий способ умножения и деления десятичных дробей на степени десяти: вы перемещаете десятичную точку на столько шагов, сколько нулей в числе 10, 100, 1000 и т. Затем я также показываю , где этот ярлык берет свое начало, используя таблицы стоимостных значений. На самом деле, перемещение десятичной точки является своего рода иллюзией, и вместо этого цифр числа перемещаются в пределах диаграммы разрядности. Это объяснение действительно может помочь учащимся понять причину «уловки» перемещения десятичной точки. В приведенном ниже уроке более подробно разъясняется ярлык, а также различные виды упражнений, словесные задачи и даже забавная загадка для учащихся.
1. Умножить.
2. Давайте еще потренируемся.
3. Теперь давайте попрактикуемся в использовании степени десяти.
4. Разделить.
6. Разделить. Подумайте о дробях
в десятичные дроби или используйте ярлык.
7. 10-фунтовый мешок орехов стоит
72 доллара. 8. Найдите цену 100 мячи для пинг-понга, если один мяч для пинг-понга стоит 0,89 доллара.
9. Разделите целые числа на 1000. Упростите окончательный ответ, отбросив все десятичные знаки в конце. нули.
10. Делить целые числа на 10 и 100.
11. Найдите одну десятую… а. $8 б. 25,50 $ г. 126 $ 12. Найдите одну сотую… а. $78 б. $4 г. 390 $
13. Пара обуви стоимостью 29 долларов была уценена на 3/10 ее цены. Какова новая цена?( Подсказка: Сначала найдите 1/10 цены. ) 14. Найдите цену со скидкой: а. Велосипед стоимостью 126 долларов продается со скидкой 2/10 его цены.
б. Сотовый телефон за 45 долларов продается со скидкой 5/100 его цены. 15. Сотая часть определенного числа
составляет 0,03. Какой номер? 16. Какой пылесос окажется дешевле? Модель Модель B сейчас стоит 75 долларов, но вы получите скидку в размере 1/4 его цены.
17. Пришло время для некоторых финальная практика. Найдите недостающие числа. Соедините букву каждой задачи с правильным ответом в клеточках и решить загадку. Есть два набора коробок. Первые коробки относятся к первому набору упражнений, а вторые — ко второму набору. Почему 7 не понял, о чем говорит 3.14?
Я также предлагаю бесплатные рабочие листы: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1000 × 0,048 = _______
10 5 × 41,59 = _____________
Перед номером нужно написать нули.
13 ÷ 10 3 = _____________
«отменяет» умножение. Если мы переместим десятичную точку в справа при умножении на 10, 100, 1000 и так далее, то это
вполне естественно, что правило деления будет работать «наоборот».
Сравните задачи в каждой коробке!
