Волк козел капуста: Загадки - Логические загадки - Загадки №: 1..20

Содержание

Задача «Волк, коза и капуста»

Удивительные находки и неразгаданные загадки

И.Г. СУХИН, Институт теории образования и педагогики РАО

Во многих математических монографиях есть страницы, посвященные истории возникновения знаменитых задач, доступных учащимся старших классов (например, Чистяков В.Д. Старинные задачи по элементарной математике — Минск, 1978). Однако практически нет работ, из которых учитель начальной школы мог бы получить исчерпывающую информацию о не менее известных старинных головоломках, представляющих интерес для учеников I–IV классов. Нам хотелось бы поделиться с читателями журнала результатами своих поисков и начать разговор о поразительной судьбе некоторых из таких задач.

В “Книге 1” труда Е.И. Игнатьева “В царстве смекалки, или Арифметика для всех: Опыт математической хрестоматии: Книга для семьи и школы” (СПб.: Тип. А.С. Суворина, 1911.

— С. 75–76) приведена одна из самых замечательных логических задач в истории человечества: “Задача 52-я. Волк, коза и капуста”:

“Крестьянину нужно перевезти через реку волка, козу и капусту. Но лодка такова, что в ней может поместиться только крестьянин, а с ним или один волк, или одна коза, или одна капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как перевез свой груз крестьянин?”

Даже если приводимая задача вам знакома, не спешите читать решение, попробуйте словно впервые поискать оптимальный маршрут и только затем ознакомьтесь с ходом решения, предлагаемым Е.И. Игнатьевым:

“Решение: Ясно, что приходится начать с козы. Крестьянин, перевезши козу, возвращается и берет волка, которого перевозит на другой берег, где его и оставляет, но зато берет и везет обратно на первый берег козу. Здесь он оставляет ее и перевозит к волку капусту.
Вслед затем, возвратившись, он перевозит козу, и переправа оканчивается благополучно”.

Данная задача бессчетное число раз публиковалась в самых различных отечественных газетах, журналах и сборниках. При этом почти во всех работах упоминается только одно решение. А ведь есть и альтернативный путь!

Вначале крестьянин опять-таки перевозит козу. Но вторым он не обязательно должен забирать волка! Можно взять капусту, отвезти ее на другой берег, оставить там и вернуть на первый берег козу. Затем перевезти на другой берег волка, вернуться за козой и снова отвести ее на другой берег. В этом случае количество рейсов (7) точно такое же, как и в опубликованном выше варианте.

Существование двух решений не отмечено ни в многократных переизданиях книги Е.И. Игнатьева, ни в других самых авторитетных источниках. В их числе: Э. Люкас “Математические развлечения: Приложение арифметики, геометрии и алгебры к различного рода запутанным вопросам, забавам и играм” (СПб.
: Изд. Павленкова, 1883. — С. 7), Н.Н. Аменицкий, И.П. Сахаров “Забавная арифметика: Хрестоматия для развития сообразительности и самодеятельности детей в семье и в школе” (М.: Изд. товарищества И.Д. Сытина, 1909. — С. 23–24), В. Аренс “Математические игры и развлечения” (СПб.: Физика, 1911. — С. 20), Б.А. Кордемский “Математическая смекалка” (М.: Государственное издательство технико-теоретической литературы, 1955. — С. 14; М.: Наука, 1991. — С. 15) и многочисленные сборники последних лет.

Это тем более удивительно, что наличие двух решений было указано, к примеру, еще в начале 20-х годов ХХ века в книге В. Литцмана “Веселое и занимательное в фигурах и числах: Математические развлечения” (М. — Пт.: Изд. Л.Д. Френкель, 1923. — С. 128–129), причем довольно подробное. Видимо, многие издатели сочли необязательным приводить оба варианта, ведь они схожи и являются по сути “зеркальными”. Но в книге для детей, особенно младшего возраста, это необходимо, иначе существенно снижается педагогическая ценность задачи!

Любопытно, что Б. А. Кордемский в решении отмечает только второй вариант и по какой-то причине не упоминает первый. Загадка? Загадка.

Очень интересен вопрос о времени возникновения данной головоломки и ее первоисточнике. Б.А. Кордемский в книге “Математическая смекалка” говорит вскользь: “Это… старинная задача; встречается в сочинениях VIII века”.

Вначале может показаться, что мы имеем дело с опечаткой, ведь первая или одна из первых отечественных публикаций задачи “Волк, коза и капуста” датирована концом ХVIII века. В фондах Российской Исторической библиотеки сохранилась книга “Гадательная арифметика для забавы и удовольствия” (СПб., 1789). На титульном листе значится: “На ижд. изд. И. Краснопольского”, что означает “на иждивении издателя И. Краснопольского”. В раритете на 62 страницах сорок одна занимательная задача. На с. 42–43 читаем: “Некоторый мужик везши с собою волка, козу и капусту приехал к реке, у берегу коей нашел столь малую лодку, что она кроме его и одного чего-нибудь из везомых им, поднимать не могла.
И так спрашивается, каким образом переправить оных через реку так, чтобы волк не съел козы, а коза капусты?” Далее приводится один вариант решения (первый).

Интересно, что в пособии болгарских авторов “Математический фольклор” (М.: Знание, 1987. — С. 180) задача о волке, козе и капусте помещена в раздел “Из математического фольклора других стран” с пометкой в скобках “Россия”.

Вернемся к истории задачи и вопросу: прав ли Б.А. Кордемский, датировав задачу восьмым веком.

По мнению ряда историков, задача имеет западные корни. В. Аренс указывает, что авторство хрестоматийной задачи приписывается Алкуину (Аренс В. Математические игры и развлечения. — СПб.: Физика, 1911. — С. 20).

В. Литцман, предлагая читателям познакомиться с задачей о переправе в книге “Веселое и занимательное о числах и фигурах” (М.: Государственное издательство физико-математической литературы, 1963. — С. 189), вскользь пишет: “У Алкуина мы находим следующий рассказ”.

Что же в наши дни известно об этой незаурядной личности? Алкуин (735–804) был ученым монахом и математиком из Ирландии, автором ряда учебников по математике. Король Карл Великий благоволил к ученым и всячески поощрял развитие наук. За королевским круглым столом нередко проводились состязания в решении хитроумных головоломок, в которых Алкуин имел возможность проявить свои незаурядные способности.

Алкуин основал Палатинскую школу в Туре (созданную для детей Карла V), принимал участие в основании университета в Париже. Добавим, что Алкуин был другом и учителем Карла Великого, его ученым советником.

Из других головоломок Алкуина наибольшую известность получили задачи 1) о гончей и зайце, 2) о покупке свиней, 3) о трех наследниках и 21 бочке, 4) о ста мерах пшеницы, 5) о быке. Но только головоломка о волке, козе и капусте до сих пор поражает воображение и детей, и взрослых. Эту и некоторые другие задачи Алкуин поместил в свой трактат “Задачи для оттачивания ума юношей”, написанный, как было принято в то время, латиницей.

Перед публикацией данной статьи очень хотелось подержать в руках текст первоисточника. А вдруг там приведены оба решения? И вот копия латинского манускрипта передо мной. Под №ХVIII легендарная задача. Сразу бросается в глаза, что решение одно — то самое, которое приводится в большинстве пособий. Но сама головоломка имеет иное название: “Задача о человеке, козе и волке”! А ее условие (если переводить близко к оригиналу) таково:

“Один человек должен был перевезти через реку волка, козу и кочан капусты. И не удалось ему найти другого судна, кроме как такого, которое могло выдержать только двоих из них. Задача, таким образом, заключалась в том, как всех перевезти на другой берег целыми и невредимыми. Скажите, кто способен: каким путем они могут перебраться на другой берег невредимыми” (перевод с латинского выполнен Е.И. Сухиной).

Так что же, все загадки разгаданы? Нет, последнее десятилетие преподносит новые сюрпризы. Вот уже в нескольких изданиях при объяснении решения данной головоломки авторы делают одну и ту же забавную ошибку. Раскроем на с. 244 пособие Е.А. Латия “365 развивающих игр и затей для маленьких детей” (М.: Эксмо-Пресс, 2001), где предлагаемое решение столь фантастично, что его следует воспроизвести дословно: “Разгадка: сперва везут волка и капусту, оставляют капусту на противоположном берегу; везут волка обратно и оставляют на берегу; забирают козу, переправляют на другой берег; там забирают капусту, везут обратно к волку и уже вместе их окончательно перевозят на другой берег”.

Если бы волка и капусту можно было везти в лодке одновременно, то переправа завершилась бы гораздо быстрее, чем указано Е.А. Латием (но по условию задачи их нельзя переправлять вместе!) В вышедшей ранее раскраске “Угадайка: Выпуск 4” (М.: Крона, 1996) волка заменили на крокодила, козу — на пирата Крюка, а капусту — на Питера Пэна, но решение аналогично предыдущему: “Сначала надо перевезти Питера и крокодила.
..” и т.д. Очевидно, что первоисточник ошибки один и тот же. Быть может вам удастся найти его?

А вдруг это Алкуин через века задумал подшутить над нами? Ничем другим я не могу объяснить то обстоятельство, что и сам первоначально при объяснении второго варианта решения указал не 7 рейсов, а 11, причем заметил свою оплошность в самый последний момент.

Да, еще не все тайны замечательной задачи разгаданы, и не исключено, что лукавая улыбка Алкуина будет преследовать не одно поколение авторов, составителей и читателей.

Где еще можно прочитать об Алкуине и его знаменитой задаче

Баврин И.И., Фрибус Е.А. Занимательные задачи по математике — М.: ВЛАДОС, 1999.

Баврин И.И., Фрибус Е.А. Старинные задачи — М.: Просвещение, 1994.

Белов В.Н. Головоломки из близкой дали // Компьютерра. — 2000. — № 1.

Депман И.Я. История арифметики — М.: Просвещение, 1965.

Леман И. Увлекательная математика — М.: Знание, 1985.

Попов Г.Н. Сборник исторических задач по элементарной математике — М. — Л.: Главная редакция научно-популярной и юношеской литературы, 1938.

НАЧАЛЬНАЯ ШКОЛА №7-2002, c. 69-70.

Волк, коза и капуста. Мастерская Эдисонов. Открытия и изобретения.
Мастерская Эдисонов
Есть такая головоломка: с одного берега реки на другой лодочнику требуется перевезти волка, козу и капусту. Лодка настолько мала, что капусту и четвероногих пассажиров можно переправлять лишь по одному. Как быть? Давай сделаем «рассуждающий» автомат.
Все части автомата крепятся на фанерной дощечке (1) размерами 180 на 300 мм. К дощечке прибей боковые рейки (2). Посредине дощечки-панели нарисуй реку. На берегах ее расположены восемь гнезд для штырьков (3). Из жести заготовь шестнадцать пластинок (4). В каждое гнездо вставь (узкой частью) по две пластинки, загни их и прикрути винтом с гайкой (например, от игры «Конструктор»).
В правом верхнем углу панели укрепи сигнальную лампочку (5). Для этого проделай в фанерной панели отверстие. Лампочка должна вворачиваться в него с небольшим усилием. Перед тем, как ее ввернуть, вложи в отверстие алюминиевую полоску (6). Вторым контактом для лампочки будет служить изогнутая пластинка (7), прикрепленная к фанерке винтом с гайкой. Рядом привяжи проволокой батарейку (8).
В качестве штырьков (3) используются небольшие гвозди. На каждый из них надень картонные кружочки (9) с надписями «волк», «коза», «капуста» и «лодочник». Штырьки в гнездах должны сидеть плотно. Это очень важно для работы автомата.
Осталось самое ответственное: собрать электрическую схему, то есть, надежно соединить проводами все гнезда, лампочку и батарейку. Поверни автомат тыльной стороной к себе и пронумеруй гнезда так, как показано на рисунке зелеными цифрами. На электрической схеме цифры тоже означают номера гнезд. Будь очень внимателен при подключении проводов. Работа значительно упростится, если соединения делать разноцветными проводами.
Вставь в гнезда штырьки в том порядке и на той стороне реки, как изображено на рисунке. Это исходное положение. Можно начинать. При неправильном действии сигнальная лампочка сразу оповестит об этом.
Попробуй сделать так: вытащить штырьки с надписями «лодочник» и «волк», а затем воткнуть их в гнезда №8 и №5 на противоположном берегу реки. Это означает, что лодочник переехал речку с волком. Лампочка загорится: неправильный ход, нельзя оставлять без присмотра козу и капусту! Перенеси на другой берег штыри с надписями «лодочник» и «капуста». Лампочка снова загорится. Опять «опасный» ход. А вот если вместо капусты лодочник повезет козу, лампочка не загорится. Ведь волк капусту есть не станет. И так каждый ход будет находиться под контролем нашего автомата. Тем, кто не знает правильного решения головоломки, играть с этим автоматом очень интересно. И не только ребятам, но даже взрослым.

Загадка про деда волка козу и капусту ответ

Волк, коза и капуста. Загадка на логику.
Эта известная головоломка есть в народном творчестве таких стран, как Италия, Румыния, Эфиопия и Зимбабве. Существует не одна ее вариация: с лисой, курицей и хлебом или с пантерой, свиньей и кашей! А Ты знаешь, как решать задачу о переправе?
14 91 т.
Итак, представь, что Ты — фермер, у которого есть маленькая лодка. С одного берега реки на другой Тебе необходимо перевезти волка, козу и капусту. Всех вместе взять нельзя — нужно переправлять каждого «пассажира» по отдельности. Но имей в виду, что когда Ты повезешь на другой берег капусту, в это время волк съест козу. А если решишь везти волка — коза скушает капусту.
Что же делать? Хорошенько поразмысли. Рейсов можно делать сколько угодно — главное, чтобы все оставалось целым и невредимым.
Ну как, удалось решить эту нелегкую задачку? Все еще нет? Ну ладно, дам одну подсказку: переправлять «пассажира» можно не только туда, но и назад!
Что же — думаю, теперь Тебе удалось перевезти всех целыми и невредимыми! Посмотри на решение задачи и проверь, все ли сходится.
Сначала нужно перевезти козу, оставив волка с капустой.
Теперь возвращаемся и забираем волка. Но оставлять волка с козой на новом берегу нельзя.
Поэтому берем козу с собой в лодку, а волк сидит на берегу одинокий и голодный.
Козу оставляем на берегу, а капусту переправляем к волку.
Возвращаемся назад и забираем козу.
Кстати, это не единственный вариант решения задачи. Вот еще один:
Везем козу туда.
Возвращаемся обратно.
Везем капусту туда.
Забираем козу назад.
Везем волка туда.
Возвращаемся за козой.
Перевозим козу туда.
Готово!
А теперь признавайся, удалось ли Тебе самостоятельно дойти до правильного решения, и если да — то каким способом? 😉

Еще больше отборных загадок найдешь тут:
Заметили орфографическую ошибку? Выделите её мышкой и нажмите Ctrl+Enter
Прослушивание: Загадка цели, волк и капуста. Загадка — переход через реку КОЗА, ВОЛК И КАПУСТА Фермер идет домой с рынка. Купил козу, капусту.
Презентация на тему: «Слушаем: Загадка, цель, волк и капуста. Загадка — переход через реку КОЗА, ВОЛК и КАПУСТА. Фермер идет домой с рынка. Он купил козу, капусту» — стенограмма презентации:
1 Прослушивание: Загадка цели, Волк и капуста
2
3 Загадка — переход через реку КОЗА, ВОЛК И КАПУСТА Фермер идет домой с рынка. Купил козу, капусту и волка. По пути домой он должен перейти реку. Он переправится через реку на лодке. Лодка маленькая и больше чем одна вещь поместится. Проблема: он не может оставить козу одну с капустой (потому что коза ее съест). Он не может оставить козу наедине с волком (потому что волк съест козу). ВОПРОС: Как фермеру получить все на другом берегу реки?
4 СЛУШАТЬ Только полный сценарий загадки Проблемный вопрос
5 ШАГИ: Представьте упражнение — Загадки (Что такое загадки?) 1.Сс слушайте загадку полностью. 2.Ss прислушиваются к ключевым словам. Затем напишите их. (Ss может потребоваться прослушать 2 раза.) 3. Практикуйтесь / Научите словарный запас Ss. 4. Снова послушайте и попробуйте представить себе сцену / картинку. Как связаны ключевые слова. СС вырисовывают свои идеи. Отдельно или весь класс. 5.Проверьте понимание — Ss (несколько) отгадывают загадку. HW: Поговорите со своими друзьями и попытайтесь найти ответ. Объясните завтра на английском (возможно, дополнительные баллы) Задание — Загадка Это хорошее упражнение на слушание. Ss = Студенты
6 Методы и теория из учебника Сноу. Групповая работа, ориентированная на учащихся; 3-4 ученика, из-за большого класса. Работать в команде; работать вместе. Учитель НЕ дает ответы. Прослушивание. После прослушивания  должно быть какое-то действие. Оценка и презентация. Покажите понимание, нарисовав время, чтобы показать конечный продукт.

.
Решение проблемы с волком, козой и капустой (форум Programming Diversions на Coderanch)
Нет, Джим Инст, вам не нужно думать о том, что происходит, когда фермер пересекает реку, или о том, что делает лодка; вы просто предполагаете, что лодка находится там, где находится фермер. На самом деле я получил 16 возможных состояний, пронумерованных от 0 до f, где самый старший бит (3-й бит = 8) представляет фермера, 2-й бит = 4 — это волк, 1-й бит = 2 — это гусь, а 0- -й бит (младший бит = 1) представляет собой зерно капусты или что-то еще.
Итак, f означает, что все четверо находятся на этой стороне реки, 0 означает, что все четыре пересеклись, 1 означает, что капуста одна на этой стороне реки, 2 означает, что гусь один на этой стороне реки и т. Д. можно было бы подумать, что это означает, что дополнение числа находится на другой стороне реки, поэтому 0 означает f на другой стороне. Тогда у вас будет инвариант thisSide + thatSide == 0xf.
По эту сторону реки есть три запрещенных штата: 3, 6, 7, где гусь ест капусту, лес — козу, или и то, и другое.Это означает, что на другой стороне есть три запрещенных состояния, 8 9 и c. Мы знаем, что 8 + 7 или 9 + 6 или c + 3 в сумме дают 0xf. Остается в общей сложности 10 разрешенных состояний. За каждым разрешенным состоянием могут следовать 1, 2 или 3 разрешенных состояния-преемника.
Правила таковы, что фермер должен переходить дорогу каждый раз в одиночку или в сопровождении одного предмета. Это эквивалентно побитовой операции XOR 8 9 a или c; если у вас есть переменные thisSide и thatSide, то одна и та же операция должна быть применена к обеим сторонам, чтобы сохранить инвариант класса.Также вы удаляете из результатов любое из шести запрещенных состояний.
Вы можете вернуть состояния обратно на английский с помощью поразрядного И: private final int FARMER = 8, WOLF = 4, GOOSE = 2, CABBAGE = 1; . = FARMER + GOOSE;
*********************************************** ***************************
В LISP он читает что-то вроде этого, предполагая, что ваш алгоритм поиска по ширине и оператор -> уже поставлено: (defparameter * farmer * ‘((fwgcR wcRfg) (fwgRc wRfgc gRfwc) (fwcRg wcRfg wRfgc cRfwg) (fgcRw gRfwc cRfwg) (fgRwc gRfwc Rfwgc) (wcRfg fwcRg fwgcR) (gRfwc fgRwc fwgRc fwcRg) (cRfwg fwcRg fgcRw) (wRfgc fwgRc fwcRg) (Rfwgc fgRwc))) (defun farmer-lmg (состояние) (-> * фермер * штат)) (width-search ‘fwgcR’ Rfwgc # ‘farmer-lmg) Аббревиатуры (очевидно) означают фермерскую волчью гусиную капусту и РЕКУ; те, кто до R, находятся на этой стороне, а те, что после R, находятся на этой стороне.Бит defun создает генератор легального хода (LMG).
*********************************************** **************************
С предоставленными нами утилитами LISP он работает, но, кажется, всегда дает мне один и тот же ответ . Я думаю, есть 4 возможных решения, но первая операция всегда заключается в том, что фермер переносит гуся, а четвертая операция всегда возвращает гуся.
[править] Незначительные орфографические исправления и значение lmg [/ править]
[30 ноября 2007 г .: Сообщение отредактировал: Кэмпбелл Ричи]
.
Волк, коза и капуста — обучающие игры
Это не только новая игра. Это тоже загадка. Надо сказать, что это очень известная головоломка.
Волк, козел и кочан на берегу реки. Недалеко от них есть лодка. Им нужно переплыть реку и добраться до другого берега реки. Но только один из них может пользоваться лодкой одновременно. Цель головоломки — перенести волка, козу и кочан на другой берег реки, и все они должны быть в безопасности.Это довольно сложно, потому что, если вы оставите волка и козу на одном берегу реки, волк съест козу. Если оставить козу и кочан вместе, коза съест капусту. Это очень интересная логическая головоломка.
Уважаемые родители, не торопитесь и не пытайтесь помочь своим детям! Неплохо, если они не могут сразу ответить на этот вопрос. Головоломка для них не очень сложная. Единственное, что им нужно, — это немного подумать.
.
Загадка про козла, капусту да волка
Вроде бы такое простое домашнее животное, но сколько про него сказок придумано! А загадка про козла, капусту и волка? Да её не только отгадывать интересно, её и рассказывать приятно, и мультфильмы по её сюжету ставить, и игры компьютерные делать!
А дело было так. Собрался как-то один мужик переправиться в лодке на другой берег реки. Да не один. Нужно было ему ещё перевезти волка, козла да вилок капусты. Так загадка про козла сказываться начинает.
А уж зачем старику волк понадобился, то никому не ведомо. Наверное, он его ещё волчонком в поле подобрал да во дворе своём вырастил. Вот и таскался за ним зверь этот, собачонкой ручной по пятам бегал. А всё одно дикое начало его внутри гвоздём сидело. Никак он спокойно не мог смотреть, как козлик серенький веселится да к хозяину ластиться. Так и норовил волчища где-нибудь с рогатым наедине остаться и скушать его, прямо сырым, с копытами и хвостом, без ножа и вилки. Вот такой это был невоспитанный и эгоистичный зверь.
Только и хозяин был не лыком шит. Натуру волчью он давным-давно разгадал, да только виду особо не показывал.
Дошли они так до реки да остановились. Все вместе они в лодке не помещаются. Может старичок только одного пассажира с собой взять либо капусту перевезти. Как тут быть?
А волк-то в душе радуется, думает: «Повезёт мужик на тот берег капусту – тут я с козлом-то и поквитаюсь! А коль меня сперва увезёт, козёл – скотина безмозглая – капусту пожуёт, хороших тумаков от хозяина схлопочет! Всё мне радость».
А вот тут-то загадка про козла и заканчивается – на самом интересном месте. Потому что, как мужик со своей задачей справился да перевёз всех на другой берег целыми и невредимыми – на то ответ вам держать, слушатели мои драгоценные.
Ответ на загадку про капусту, козла и волка
Сложная перед мужиком задача стояла. Нельзя никак ни козла с капустой оставить, ни волка с козлом наедине. Вот такая вот загадка про козла, тут и логика нужна, и креативность мышления.
Только быстро мужик сообразил: погрузил на лодку скотинку рогатую, а волка капусту сторожить оставил. Да-да, так прямо и сказал: «Сидеть, Шарик! – он такую обидную кличку дикому зверю дал, прямо беда от неё волку. – Сидеть, да капусту сторожить!»
Только отвёз мужик козла, назад повернул. Волк снова слюну сглотнул… Уж сейчас-то старик точно его к козлу повезёт! И правда, взял мужик Шарика на этот раз. Только довёз на другой берег, волк прыг-скок с лодки, да и сел скромнёхонько так, будто бы ничего дурного у него и в мыслях-то нет.
Но старика на мякине не проведёшь! Он козла цап у волка из-под носа – и снова в лодку. Вёсла взял в руки да и назад поплыл. У волка чуть глаза из орбит не повылазили: старик-то совсем рехнулся, коль козла к капусте везёт!
Перевёз мужик животинку, высадил на берег. А капусту забрал с собой. Козлик от удивления даже блеять перестал. Всё понять пытался, зачем это хозяин его туда-сюда возит. Да где ж ему? Он хоть и с рогами, а барану брат двоюродный, потому и умом они в чём-то схожи.
А старик капусту волку сгрузил. Потом снова команду свою обидную ему повторил, да за козлом отправился. Пробовал волк капусту зубами куснуть, да так ему противно стало, что взвыл он от обиды горькой. С тех пор и воет он частенько – вспоминает, как мужик его перехитрил.
Игра «Восстанови загадку»
Если собирается компания, можно развлечь их, предложив творческое задание. Для него берётся не очень известная загадка, выписываются из неё все существительные. Ответ ставится в самое начало списка.
Участникам конкурса «Восстанови загадку» предлагается сложная работа. Справятся ли они? Ведь практически невозможно догадаться по предложенным словам, что это за загадка: козел, бородой, лыко, лаптей.
А на самом деле она звучит так.
Кто длинной бородой своей трясёт, лыко с лип дерёт, а лаптей-то не плетёт?
А ответ все помнят, ведь это слово стояло в строке первым. Это, конечно же, козел!
Волк, коза, капуста и японские маньяки
Классический вариант:
«Крестьянину нужно перевезти через реку волка, козу и капусту. Но лодка такова, что в ней может поместиться только крестьянин, а с ним или один волк, или одна коза, или одна капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как перевез свой груз крестьянин?»
Два варианта решения и история задачи — аж с VIII века:
http://suhin.narod.ru/mat4.htm
А вот усложнённый вариант с большим количеством действующих лиц. Японский якобы тест при приёме на работу:
http://freeweb.siol.net/danej/riverIQGame.swf
Для начала игры жмем большую синюю кнопку и перевозим всех на другой берег, следуя несложным правилам:
1. Полицейский не может оставлять преступника с людьми одного.
2. Папа не может оставлять сыновей одних с мамой, а мать — дочерей с папой.
3. Дети одни не могут плавать на плоту.
4. Плот сам по себе не возвращается и берег на борт не более двух человек.
Меня бы точно не приняли на ту японскую работу. Вообще, плохо решаю головоломки: обычно не хватает терпения разобраться самой, лезу в ответ. В данном случае ответ быстро нашёлся в гугле (см. ссылку ниже). Но вот честно: при решении больше всего сбивали с толку кое-какие, с моей точки зрения, дикие несообразности в правилах. Полицейский не может оставлять преступника с людьми без своего присмотра — но может оставлять его одного, без людей! Бежать там что-ли некуда? Дети не могут находиться с родителем противоположного пола без второго родителя. Ну, маньяческая семейка! Возможно, поэтому едут туда же, куда полицейский с преступником? При нарушении правил падает зелёный листик, звучит печальная нота и кто-то кого-то лупит по башке — видимо, со смертельным исходом. Чтобы переправить эту милую компанию, нужно 17 рейсов:
http://www.netlore.ru/yaponskie-volk-koza-i-kapusta
Инстересно, за сколько бы переправились вменяемые люди? То есть, переформулирую: «Полицейского и преступника разделять нельзя. Дети должны всегда находятся под присмотром кого-нибудь из взрослых (родителей или полицейского)». У меня получилось 13 рейсов.
Задачи о переправах | ИНФОРМАТИКА
Примеры решения задач.
Задача. Переправа через реку.
Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться на другой берег отцу и сыновьям?
Решение.
Вначале переправляются оба сына.
Один из сыновей возвращается обратно к отцу.
Отец перебирается на противоположный берег к сыну.
Отец остается на берегу, а сын переправляется на исходный берег за братом, после чего они оба переправляются к отцу.
Задачи для самостоятельного решения.
1. Волк, коза и капуста. На берегу реки стоит крестьянин с лодкой, а рядом с ним находятся волк, коза и капуста. Крестьянин должен переправиться сам и перевезти волка, козу и капусту на другой берег. Однако в лодку кроме крестьянина помещается либо только волк, либо только коза, либо только капуста. Оставлять же волка с козой или козу с капустой без присмотра нельзя — волк может съесть козу, а коза — капусту. Как должен вести себя крестьянин?
2. Два солдата подошли к реке, по которой на лодке катаются двое мальчиков. Как солдатам переправиться на другой берег, если лодка вмещает только одного солдата либо двух мальчиков, а солдата и мальчика уже не вмещает?
3. Пятеро разведчиков подошли к реке, через которую лежал их дальнейший путь. Река была глубокая, а
моста через нее не было. У берега стояла лодка с сидящими в ней двумя мальчиками. Разведчики попросили мальчиков перевезти их всех на другой берег. Составьте алгоритм переправы, если известно, что лодка вмещает только одного солдата либо двух мальчиков, а солдата и мальчика уже не вмещает. За сколько рейсов можно это сделать? За рейс следует считать движение лодки в одном направлении.
4. На реке во время половодья оторвало от берега и унесло большую лодку, на которой перевозили через реку окрестных жителей. У перевозчика осталась лишь одна маленькая лодка, на которой молено переправить либо одного взрослого, либо двух мальчиков, которые всегда помогали перевозчику переправлять народ. В это время к реке подошла партия землекопов. Поразмыслив немного, все землекопы ухитрились переправиться через реку именно на этой лодке. Как им удалось это сделать?
5. Трем неутомимым путешественникам — Андрею, Михаилу и Олегу — надо было переправиться на лодке, выдерживающей массу не более 100 кг, с одного берега реки на противоположный. Андрей знал результат своего недавнего взвешивания — 54 кг и своего друга Олега — 46 кг. Зато Михаил весил около 70 кг. Как им надо было действовать наиболее рациональным образом, чтобы переправиться через реку?
6. Двум англичанам, путешествующим в дебрях Амазонки, и двум их проводникам из местного племени требуется переправиться на противоположный берег реки. В распоряжении путешественников имеется небольшая надувная лодка, способная вместить только двух человек. Англичане подозревают, что их проводники из племени людоедов, и чувствуют себя в безопасности только тогда, когда находятся вдвоем. Как устроить безопасную переправу?
7. К реке одновременно подошли три купца и три разбойника. Всем необходимо было переправиться на другой, противоположный берег. У берега стояла лодка, которая могла вместить только двух человек. Купцы боязливо поглядывали на разбойников, так как знали, что во время переправы могло всякое случиться. Если во время переправы на том или ином берегу число купцов и разбойников будет одинаковым, то разбойники не тронут купцов; если же число разбойников превысит число купцов хотя бы на одного человека, то разбойники убьют купцов. Перед купцами стояла сложная задача, но она легко была ими решена — все перебрались на тот берег и жертв не было. Как сумели переправиться на тот берег купцы и разбойники и сколько рейсов туда и обратно совершила лодка? За рейс следует считать движение лодки в одном направлении.
8. У причала стояла лодка, которая могла перевозить не больше двух человек. К реке подошли четверо, которым было необходимо переправиться на противоположный берег. Все они переправились через реку без посторонней помощи и продолжили свой путь, причем лодку поставили на тот же причал, откуда ее и взяли. Возможно ли это?
9. Дело было в Америке. Как-то раз подошли к реке англичанин, негр и индеец, каждый со своей женой. Всем нужно было переправиться на другой берег. В их распоряжении была только одна лодка (да и та без гребца), способная вместить лишь двоих. Договорившись между собой, мужчины решили было приступить к переправе, как вдруг выяснилось, что ни одна из жен не желает переправляться в лодке с чужим мужем или оставаться на берегу в мужском обществе без своего мужа. Мужья призадумались, но все же сумели догадаться, как выполнить желание своих жен. Как они сумели переправиться через реку?
10. Как крестьянину перевезти в лодке с одного берега на другой козла, капусту, двух волков и собаку, если известно, что волка нельзя оставлять без присмотра с козлом и собакой, собака в «ссоре» с козлом, а козел «неравнодушен» к капусте? В лодке только три места, поэтому можно брать с собой не более двух животных или одно животное и капусту.
Волк, коза и капуста — SCoon the Crazy — ЖЖ
Чт, 21 июн, 2007, 17:34

Волк, коза и капуста Второй раз в жизни сижу (лежу?) на больничном. В свободное от кодинга (ага, работу за меня никто не сделает) время в голову лезут глупые мысли. Разумеется — навеянные кодингом.
Например, все знают десткую загадку:
Вы находитесь на берегу реки. Перед вами — обычныая весельная лодка (с веслами, разумеется), кочан капусты, козел и волк. Будем считать, что волк и козел дрессированные и в вашем присутствии козел не ест капусту, а волк не есть козла. Ваша задача — перевезти всех троих на другую сторону. Проблема осложнена тем, что в лодку Вы можете взять с собой только 2 объекта. Например, волка и капусту (кочан, вероятно, очень крупный).
Итак, вопрос: сколько «ходок» через реку нужно сделать, чтобы выполнить перевоз? Помните, что вы уже взрослые люди.
Update: в лодку можно брать только одного, как меня справедливо поправили ниже.
Чт, 21 июн, 2007 14:12 (UTC)

netklon В лодку можно взять только одного.
Чт, 21 июн, 2007 15:18 (UTC)

scoon_the_crazy Thanx! 🙂
А варианты решений?
Пт, 22 июн, 2007 07:20 (UTC)

netklon Ну решение только одно: изолировать среднее звено пищевой цепи.
Сначала перевозим козла. Потом волка, козла везем обратно, оставляем, везем капусту, возвращаемся за козлом.
Пт, 22 июн, 2007 07:40 (UTC)

netklon Почита комменты. Какой же я зануда.
Пт, 22 июн, 2007 15:13 (UTC)

scoon_the_crazy Однако решение получилось — среди всей группы — наиболее нестандартным. 🙂
Чт, 21 июн, 2007 14:18 (UTC)

ylevdik 1. Та же бодяга: не имеет значения, что В МОЁМ ПРИСУТСТВИИ козёл не ест капусту, а волк не ест козла — потому что на берегу они всё равно друг друга будут все жрать.
2. Вёсла есть? А жахнуть волка и козла по башкам их дрессированным можно? Чтобы они отрубились на нужное время? 🙂
3. Если забыть о том, что мы ВЗРСЛЫЕ ЛЮДИ, то, конечно же, надо просто взять с собой капусту и волка, потом порожняком вернуться за козлом, оставив волка наедине с капустой. Итого — три ходки, одна из которых — порожняя. 🙂
4. Если вспомнить о том, что мы ВЗРОСЛЫЕ ЛЮДИ, то кочан капусты можно обвязать верёвкой (которая на носу у каждой лодки есть) и пустить капусту плыть за бортом, следом за лодкой, а дрессированных животных везти в лодке с собой — и обойтись, таким образом, одной ходкой. 🙂
5. Если ещё вспомнить, что всё это навеяно КОДИНГОМ, то ни одно решение (из приведённых) не является ожидаемым и удовлетворительным. 🙂
Чт, 21 июн, 2007 15:16 (UTC)

scoon_the_crazy Мои вариантs:
1. Жжахнуть веслом волка по башке. Причем так, чтобы наверняка сдох — к чему мне сюрпризы? Козла за хвост привязать к лодке. В лодке взять дохлого волка и не менее дохлую капусту.
2. Живого волка привязать за хвост к лодке. Капусту и козла — в лодку. Этот вариант хуже, поскольку живой волк может быть неадекватен, а дохлый плохо плавает.
Я обдумывал вариант с привязыванием капусты, но здесь больше возни.
Чт, 21 июн, 2007 16:00 (UTC)

ylevdik Есть ещё вариант: из козлятины с капустой получится вполне нормальный польский бигос. Его и берём с собой в лодку. А волка привязываем к лодке снаружи, чтобы потонул по дороге, собака бешенная!
Чт, 21 июн, 2007 19:33 (UTC)

libby_long веревкой привязать козла и волка к лодке и подгонять их веслами, чтоб веселее плыли. капусту, так уж и быть — в лодку сложить.
Чт, 21 июн, 2007 19:35 (UTC)

libby_long Хотя нет, козла надо привязать первым, а волка вторым — тогда и веслами подгонять не надо будет — сами поплывут, как миленькие
Чт, 21 июн, 2007 19:37 (UTC)

libby_long а если перед козлом подвесить капусту — скорость передвижения увеличится
Чт, 21 июн, 2007 21:55 (UTC)

zerkms
Пт, 22 июн, 2007 06:40 (UTC)

ex_jcell
Кстати на чём и под что ты программируешь ?
Пт, 22 июн, 2007 15:12 (UTC)

scoon_the_crazy Не поверишь: непосредственно сейчас — на PHP. Оттого, наверное, и мысли странные в голову лезут.
В так — Java, C#, Ruby.
Пн, 25 июн, 2007 11:05 (UTC)

ex_jcell
О ужас, не тоскливо было перейти на php ?
Волк, коза и капуста
Головоломки уходят в прошлое. Одна из самых известных головоломок — это загадка «Волк, козел и капуста», которая восходит как минимум к 9 ^{-м и} годам. Известная также как «загадка лиса, курица и зерно», «загадка лисы, гуся и мешка с фасолью», «загадка пантеры, свиньи и каши» и многие другие версии, ее можно найти во многих фольклорах Африки. Азия, Европа, Америка и Австралия. Загадка заключается в следующем. Фермер идет на рынок и покупает волка, овцу и капусту.По пути домой он должен пересечь реку на лодке с одного берега на другой. Лодка может перевозить только фермера и еще одну вещь — волка, козу или капусту, поэтому фермеру нужно будет сделать несколько поездок, чтобы все три лодки перебрались на другой берег. Во время катания на лодке ему всегда придется оставлять две вещи самостоятельно на берегу реки. По понятным причинам волка нельзя оставлять наедине с козой — он ее сожрет. Козу нельзя оставлять с капустой, потому что она ее съест.Как же тогда фермер может перевезти всех троих на другой берег реки, оставив их всех нетронутыми?
Подождите! Попробуйте решить эту головоломку, прежде чем читать дальше.
Волк, овца и капуста — раствор
Очевидно, что фермер должен сначала отвезти козу, оставив волку с капустой. Затем он возвращается в одиночку к лодке либо над капустой, либо над волком. На самом деле не имеет значения, какой именно. Допустим, он забирает волка. Он не может оставить волка с козой, пока он возвращается за капустой, поэтому он оставляет волка и уносит козу обратно в исходный банк.Он оставляет козу, собирает капусту, перегоняет ее на лодке и оставляет на дальнем берегу вместе с лисой. Наконец, он возвращается один, чтобы перевезти козу на другой берег.
Обсуждение
Эта так называемая головоломка «пересечение реки» представляет собой алгоритмическую головоломку. Он просит нас найти алгоритм, который решает данную проблему. Существует множество вариаций головоломки с волком, козой и капустой. Вот одна вариация. Вы можете это решить? Публикуйте свои решения в комментариях! Вам также предлагается публиковать свои собственные варианты этой головоломки, чтобы мы все попытались их решить. Фермер должен переправить через реку лису, курицу, гусеницу и капусту. Лодка может вместить фермера и две лишние вещи. Нельзя оставлять лису с курицей, курицу нельзя оставлять с гусеницей, а гусеницу нельзя оставлять с капустой. Как он может перевезти все на другой берег, оставив все в целости и сохранности?
© Davidson Institute of Science Education, Weizmann Institute of Science
#! / Usr / bin / python # D.Vrajitoru, C463 / B551 Весна 2008 г. # Реализация поиска в глубину для решения # коза-волк-капуста-пазл. # Проблема: мужчина перевозит козу, волка и капусту. Он # должен пересечь реку и иметь лодку, на которой может быть только 1 предмет # вне себя за раз. Он не может оставить козу одну на одной # берег реки с капустой, потому что коза съест # капуста. То же самое с волком и козой. Найдите последовательность # действий, которые мужчина может выполнить, чтобы навести друг друга # сторона в безопасности.entity = [‘коза’, ‘волк’, ‘капуста’] путь = [] # Определяет, кто кого может есть def eats (x, y): если x == ‘коза’ и y == ‘капуста’: вернуть True elif x == ‘волк’ и y == ‘коза’: вернуть True еще: вернуть ложь # Определяет, можно ли оставить пару сущностей одну на одной стороне № реки. def safe_pair (x, y): если ест (x, y) или ест (y, x): вернуть ложь еще: вернуть True # Возвращает состояние символа who в словаре al. Это # возвращает его значение, а не ссылку на него, поэтому его можно использовать для # тестирование, но без изменений.Если символ, не входящий в список # возвращает ноль. def state_of (кто, государство): пытаться: вернуть состояние [кто] кроме KeyError: состояние [who] = Ложь вернуть ложь # Проверяет, безопасно ли состояние, определенное как словарь. Если # коза на той же стороне, что и человек, значит, мы в безопасности. В противном случае, если # капуста или волк тоже на другой стороне, значит мы не # безопасно. def safe_state (состояние): если state_of (‘человек’, состояние) == state_of (‘коза’, состояние): вернуть True elif state_of (‘коза’, состояние) == state_of (‘волк’, состояние): вернуть ложь elif state_of (‘коза’, состояние) == state_of (‘капуста’, состояние): вернуть ложь еще: вернуть True # Перемещает объект с одной стороны на другую в состоянии al. Это # список мутаторов. Позиции всех сущностей определены 0 # и 1, поэтому ход заменяет текущую позицию на 1 — it. Это # возвращает результирующий список. def move (кто, государство): если указано [who] == ‘left’: заявить [who] = «правильно» еще: состояние [who] = ‘left’ состояние возврата # Проверяет, достигло ли состояние цели. Это тот случай, если все # четыре объекта находятся на другой стороне. def goal_reach (состояние): если не указать: вернуть ложь return (state_of (‘человек’, состояние) == ‘право’ и state_of (‘коза’, состояние) == ‘право’ и state_of (‘волк’, состояние) == ‘право’ и state_of (‘капуста’, состояние) == ‘право’) # Проверяет, является ли ребенок безопасным состоянием для перехода, и если это так, добавляет # это в список состояний.def check_add_child (дочерний элемент, list_states): если safe_state (дочерний): list_states.append (дочерний) вернуть list_states def expand_states (состояние): children = [] child = state. copy () # мужчина тоже может двигаться один двигаться (‘мужчина’, ребенок) check_add_child (ребенок, дети) для Ent в объекте: # Переместите один объект в ту же сторону, что и человек если state_of (ent, state) == state_of (‘человек’, состояние): child = state.copy () двигаться (‘мужчина’, ребенок) двигаться (энт, ребенок) check_add_child (ребенок, дети) #еще: # печать «небезопасное состояние», ребенок вернуть детей # Ищет решение из начального состояния def search_sol (состояние): дорожка.добавить (состояние) next = state.copy () while next, а не goal_reach (next): nl = expand_states (далее) следующий = {} для ребенка в nl: если нет (ребенок в пути): следующий = ребенок path.append (далее) перерыв вернуться дальше # Инициализация глобальных переменных initial_state = {} initial_state [‘человек’] = ‘влево’ для е в объекте: initial_state [e] = «влево» #print initial_state # {‘капуста’: ‘левый’, ‘волк’: ‘левый’, ‘коза’: ‘левый’, ‘человек’: ‘левый’} # Чтобы увидеть, как выглядят все дочерние состояния из текущего print «Расширяющееся начальное состояние» печать expand_states (начальное_состояние) # Построить полное решение после оценки предыдущих утверждений print «Поиск решения из начального состояния:» напечатать search_sol (начальное_состояние) # Оценить путь к переменной, чтобы увидеть решение в обратном направлении. print «Полный путь:» для s в пути: печать с
Добро пожаловать в классическую головоломку «Фермер, волк, коза и капуста»
Описание:
Фермер пытается пронести волка, козу и капусту через река с помощью протекающей лодки. Однако, поскольку лодка протекает, он может носить с собой по одному предмету за раз. Проблема в том, что волк и козел держитесь вместе, волк съест козу; а если коза и капуста держится вместе, коза ее съест.Найти путь который помогает фермеру перенести троих всех на правый берег реки
Инструкция по использованию схемы для решения головоломки:
Четыре переключателя представляют фермера, волка, козу и капусту. Когда переключатель выключается, это означает, что элемент, который он представляет, находится на левом берегу. реки. Когда переключатель включается, это означает, что элемент, который он представляет, включен. правый берег. Светодиод в конце цепи включится, чтобы сообщить вам, есть ли коза и волк, или коза, и капуста остаются вместе без фермера. В процессе найти способ помочь фермеру перенести все его вещи на правый берег реки, пожалуйста убедитесь, что светодиод не горит. Если светодиод загорается, значит, ваше решение неверное.
{ «ширина»: 800, «высота»: 600, «showToolbox»: правда, «ящик для инструментов»:[ {«введите»}, {«введите из»}, {«type»: «DC»}, {«type»: «LED»}, {«type»: «PushOff»}, {«type»: «PushOn»}, {«type»: «Toggle»}, {«type»: «BUF»}, {«тип»: «НЕ»}, {«тип»: «И»}, {«тип»: «И-НЕ»}, {«тип»: «ИЛИ»}, {«type»: «NOR»}, {«type»: «EOR»}, {«тип»: «ENOR»}, {«type»: «OSC»}, {«type»: «7seg»}, {«type»: «16seg»}, {«тип»: «4bit7seg»}, {«type»: «RotaryEncoder»}, {«type»: «BusIn»}, {«type»: «BusOut»}, {«тип»: «RS-FF»}, {«type»: «JK-FF»}, {«type»: «T-FF»}, {«type»: «D-FF»}, {«type»: «8bitCounter»}, {«type»: «HalfAdder»}, {«type»: «FullAdder»}, {«тип»: «4bitAdder»}, {«тип»: «2to4BinaryDecoder»}, {«тип»: «3to8BinaryDecoder»}, {«тип»: «4to16BinaryDecoder»} ], «устройства»: [ {«type»: «DC», «id»: «dev0», «x»: 24, «y»: 312, «label»: «DC»}, {«type»: «Toggle», «id»: «dev1», «x»: 144, «y»: 208, «label»: «farmer»}, {«type»: «Toggle», «id»: «dev2», «x»: 144, «y»: 272, «label»: «wolf»}, {«type»: «Toggle», «id»: «dev3», «x»: 144, «y»: 336, «label»: «goat»}, {«type»: «Toggle», «id»: «dev4», «x»: 144, «y»: 408, «label»: «капуста»}, {«type»: «AND», «id»: «dev5», «x»: 280, «y»: 128, «label»: «AND»}, {«type»: «AND», «id»: «dev6», «x»: 280, «y»: 208, «label»: «AND»}, {«type»: «NOT», «id»: «dev7», «x»: 280, «y»: 56, «label»: «NOT»}, {«type»: «AND», «id»: «dev8», «x»: 376, «y»: 88, «label»: «AND»}, {«type»: «AND», «id»: «dev9», «x»: 376, «y»: 168, «label»: «AND»}, {«type»: «NOT», «id»: «dev10», «x»: 280, «y»: 384, «label»: «NOT»}, {«type»: «NOT», «id»: «dev11», «x»: 280, «y»: 448, «label»: «NOT»}, {«type»: «NOT», «id»: «dev12», «x»: 280, «y»: 520, «label»: «NOT»}, {«type»: «AND», «id»: «dev13», «x»: 376, «y»: 416, «label»: «AND»}, {«type»: «AND», «id»: «dev14», «x»: 376, «y»: 488, «label»: «AND»}, {«type»: «AND», «id»: «dev15», «x»: 464, «y»: 352, «label»: «AND»}, {«type»: «AND», «id»: «dev16», «x»: 464, «y»: 448, «label»: «AND»}, {«type»: «OR», «id»: «dev17», «x»: 600, «y»: 264, «label»: «OR»}, {«type»: «OR», «id»: «dev18», «x»: 536, «y»: 400, «label»: «OR»}, {«type»: «OR», «id»: «dev19», «x»: 528, «y»: 128, «label»: «OR»}, {«type»: «LED», «id»: «dev20», «x»: 648, «y»: 264, «label»: «LED»}, {«type»: «PushOn», «id»: «dev21», «x»: 80, «y»: 312, «label»: «PushOn»} ], «коннекторы»: [ {«от»: «dev1. in0 «,» to «:» dev21.out0 «}, {«from»: «dev2.in0», «to»: «dev21.out0»}, {«from»: «dev3.in0», «to»: «dev21.out0»}, {«from»: «dev4.in0», «to»: «dev21.out0»}, {«from»: «dev5.in0», «to»: «dev2.out0»}, {«from»: «dev5.in1», «to»: «dev3.out0»}, {«from»: «dev6.in0», «to»: «dev3.out0»}, {«от»: «dev6.in1», «до»: «dev4.out0»}, {«from»: «dev7.in0», «to»: «dev1.out0»}, {«from»: «dev8.in0», «to»: «dev7.out0»}, {«from»: «dev8.in1», «to»: «dev5.out0»}, {«from»: «dev9.in0», «to»: «dev7.out0»}, {«от»: «dev9.in1 «,» to «:» dev6.out0 «}, {«from»: «dev10.in0», «to»: «dev2.out0»}, {«from»: «dev11.in0», «to»: «dev3.out0»}, {«from»: «dev12.in0», «to»: «dev4.out0»}, {«from»: «dev13.in0», «to»: «dev10.out0»}, {«от»: «dev13.in1», «до»: «dev11.out0»}, {«from»: «dev14.in0», «to»: «dev11.out0»}, {«from»: «dev14.in1», «to»: «dev12.out0»}, {«from»: «dev15.in0», «to»: «dev1.out0»}, {«from»: «dev15.in1», «to»: «dev13.out0»}, {«from»: «dev16. in0″, «to»: «dev1.out0»}, {«from»: «dev16.in1», «to»: «dev14.out0»}, {«от»: «dev17.in0 «,» to «:» dev19.out0 «}, {«from»: «dev17.in1», «to»: «dev18.out0»}, {«from»: «dev18.in0», «to»: «dev15.out0»}, {«from»: «dev18.in1», «to»: «dev16.out0»}, {«from»: «dev19.in0», «to»: «dev8.out0»}, {«from»: «dev19.in1», «to»: «dev9.out0»}, {«from»: «dev20.in0», «to»: «dev17.out0»}, {«от»: «dev21.in0», «до»: «dev0.out0»} ] }
Решение проблемы волчьей козьей капусты с помощью F # — статьи TechNet — США (английский)
Я изучаю язык F #. В рамках этого путешествия я решил написать решение проблемы волка, козы и капусты на F #.
Было немного сложно начать, потому что я просто не мог мыслить в терминах функционального программирования и F #. Эти две статьи помогли мне начать работу
http://www.paulbutcher.com/2007/09/escape-from-zurg/
http://web.engr.oregonstate.edu/~erwig/papers/Zurg_JFP04.pdf
Мне тоже было трудно прочитать эти две статьи, потому что они написаны на Ruby и Haskell, но я получил общее представление о том, как построить решение таких проблем.
Моим первым шагом было определить список элементов, которые нужно переместить с левого берега на правый берег, а также констант
1. let Items = [ «Волк» ; «Коза» ; «Капуста» ]
2.
3. let DeadlyCombinations = [ установить [ «Волк» ; «Коза» ]; комплект [ «Коза» ; «Капуста» ];]

Здесь Items — это просто список с 3 строками.DeadlyCombinations — это также список, состоящий из двух наборов. Эти наборы определяют предметы / животных, которых нельзя оставлять одних ни на одном берегу.
Нам также нужна функция, чтобы проверить, принадлежит ли список смертельным комбинациям или нет. для этого напишем следующую функцию
1. let isMoveDeadly list1 =
2. пусть listSet = комплект list1
3. Список.существует (весело n -> n = listSet) DeadlyCombinations

Затем мне нужна логика для перемещения Предмета из левого берега в правый. для этого я написал метод под названием MoveRight (означает перемещение объекта с левого берега на правый берег).
01. let rec MoveRight items =
02. сопоставить предметы с
03. | [] -> []
04. | голова :: хвост ->
05. если (isMoveDeadly tail), затем
06. MoveRight хвост @ [голова]
07. остальное
08. Console.WriteLine ( "Идет для перемещения » + головка)
09. хвост

здесь MoveRight — имя функции.rec означает, что эта функция будет вызываться рекурсивно, и она принимает животных в качестве параметра. здесь вы можете видеть, что F # автоматически определяет тип животных, для которых я использую логику сопоставления. Тип, который Для животных предполагается, что это List.
Первая строка простая. если переданный список пуст, вернуть пустой список и выйти. В противном случае разделите список на голову, а остальные — на хвост.
Наша цель — двигать головой только в том случае, если хвост не смертельно опасен. в противном случае нам нужно выбрать другой элемент из списка.
Итак, мы выбираем голову из списка и смотрим, является ли хвост смертельным.если да, мы помещаем голову в конец списка, а затем рекурсивно вызываем функцию снова, чтобы второй элемент был выбран как голова.
Если хвост не смертельный, то мы эффективно переместили головной элемент с левого берега на правый.
Поскольку один элемент перемещается из левого берега в правый, мы возвращаем оставшийся список в качестве вывода.
Иногда нам может потребоваться переместить предмет с правого берега на левый берег реки, потому что комбинация на правом берегу реки может оказаться смертельной
01. пусть MoveLeft животные =
02. let RightList = ListDiff animals Животные
03. let ShouldTakeAnimal = isMoveDeadly RightList
04. если (ShouldTakeAnimal), затем
05. let x = List.head RightList
06. Консоль.WriteLine ( "Переход к переместить " + x + " назад " )
07. [x]
08. остальное
09. Console.WriteLine ( "Фермер идет только назад " )
10. []

Когда предмет перемещается с левого берега на правый, фермер должен вернуться, чтобы переместить следующий предмет с левого берега на правый.но это не так просто, потому что если фермер покидает правый берег и комбинация там смертельна, то предметы будет уничтожен. Итак, нам нужно определить, может ли фермер уйти с правого берега на левый в одиночку … или он должен взять с собой какой-то предмет.
Для этого мы пишем нашу функцию MoveLeft (перемещение с правого берега реки на левый).
Поскольку мы не создаем второй список для элементов на правом берегу реки, нам нужно взять разницу между основным списком элементов на top с текущим списком элементов на левом берегу, чтобы получить список элементов на правом берегу. Это делается с помощью следующих функция, которая используется в функции MoveLeft выше
1. let ListDiff list1 list2 = List.filter (fun n -> List.forall (fun x -> x <> n) список1) список2

Первый оператор if определяет, может ли фермер уйти один или он должен переместить предмет с правого берега на левый. это делается путем определения того, является ли комбинация на правом берегу реки смертельной. если да, то фермер не может путешествовать один, и он должен взять с собой предмет.Если комбинация не смертельна, фермер может путешествовать один.
Имея все эти функции, мы можем написать главную функцию, которая решит загадку. Главная функция должна продолжать перемещать фермера между левым и правым берегами, рекурсивно вызывая себя, пока загадка не будет решена. Моя основная функция выглядит как
01. let rec Решить направление животные =
02. матч животных с
03. | [] -> Console.WriteLine ( "Решено" )
04. | _ ->
05. направление совпадения с
06. | Влево -> Решить вправо (Перемещение животных вправо)
07. | Вправо -> Решить влево (животные @ (MoveLeft animals))

Здесь Solve — рекурсивная функция, которая принимает два параметра: направление и список животных на левом берегу.Начнем с передачи всего списка элементов в качестве параметра.
Нам нужно создать размеченное направление с довольно простым
1. тип Направление =
2. | Левый
3. | Правый

Логика функции решения следующая.
если список животных слева пуст, загадка решена. если нет, то проверьте, где находится фермер, если фермер слева, затем переместите животное с левого берега на правый, вызвав MoveRight, и если фермер находится на правом берегу, затем вызовите функцию MoveLeft.(функция moveleft переместит фермера обратно на левый берег в одиночку … или с животным, если комбинация смертельна).
Наконец, мы вызываем нашу главную функцию в основном методе
1. []
2. let main args =
3. Решить левые животные
4. 0

Результат программы:
Этот пример был хорош, потому что он заставил меня задуматься о
1.сопоставление с образцом
2. рекурсивное сокращение входного набора с помощью head :: tail
3. Разбиение ограничений задачи на мелкие функции.
Но что я не мог сделать в этой проблеме, так это сделать некоторые закрытие и другие функциональные вещи, такие как каррированные функции. Я надеюсь сделать это в следующих задачах, которые я решу.
Если вы хотите улучшить мой код для решения этой проблемы, не стесняйтесь редактировать эту страницу и улучшать код. вот весь листинг кода
открытая система
(*
)
Направление типа определяет, в каком направлении человек это настоящее время.
Слева означает, что Человек это присутствует на левой стороне берега.
Право означает человека это присутствует на правой стороне банка.
*)
тип Направление =
| Левый
| Правый
(*
Главный список животных
*)
let Животные = [ «Волк» ; «Коза» ; «Капуста» ]
let DeadlyCombinations = [ установить [ «Волк» ; «Коза» ]; комплект [ «Коза» ; «Капуста» ];]
пусть isMoveDeadly list1 =
пусть listSet = комплект list1
Список. существует (весело n -> n = listSet) DeadlyCombinations
let rec MoveRight animals =
сопоставьте животных с
| [] -> []
| голова :: хвост ->
если (isMoveDeadly tail), затем
MoveRight tail @ [голова]
еще
Консоль.WriteLine ( «Собираюсь переехать» + головка)
хвост
let ListDiff list1 list2 = List.filter (fun n -> List.forall (fun x -> x <> n) list1) list2
пусть MoveLeft животные =
let RightList = ListDiff animals Животные
let ShouldTakeAnimal = isMoveDeadly RightList
если (ShouldTakeAnimal), затем
пусть x = Список. голова RightList
Console.WriteLine ( «Собираюсь переехать» + x + "задний" )
[x]
еще
Console.WriteLine ( «Фермер возвращается один» )
[]
let rec Решить направление животные =
сопоставьте животных с
| [] -> Консоль.WriteLine ( «Решено» )
| _ ->
направление совпадения с
| Влево -> Решить вправо (Перемещение животных вправо)
| Вправо -> Решить влево (животные @ (MoveLeft animals))
[]
let main args =
Решить левые животные
0

козья капуста волк загадка ответ
Проблема волка, козы и капусты. Таким образом, в лодке одновременно может быть только два объекта (фермер и еще один). Он должен был хорошо о них заботиться, так как волк хотел бы попробовать кусок козы, если бы ему представилась такая возможность, в то время как козел, похоже, жаждал вкусной капусты. Есть волк, коза и капуста. Человек хочет переправить их через реку в дом друзей. Есть лодка, на которой можно забрать человека и одно из трех животных. Он может вернуться, чтобы забрать каждого из них, но если он оставляет козу с капустой, коза ее съест; если он оставит волка с козой, волк съест ее.Как он переправит всех трех животных через реку, чтобы ни один из них не был ****. Если волк и коза останутся одни на одном берегу, волк съест козу. Нельзя держать Козу и капусту вместе (потому что Коза ее съест) или Козу с Львом (потому что Коза будет съедена). Река. Сложность головоломки может возникнуть из-за ограничений на то, какие или сколько предметов можно транспортировать одновременно, или какие или сколько предметов можно безопасно оставить вместе. В его лодке достаточно места для человека плюс волк, коза или капуста.В исходной загадке человек должен пересечь реку на лодке, которая может удерживать только его и еще один объект. Козел-пастух и капуста на одном берегу. Есть лодка с максимальной вместимостью два человека. Если он возьмет волка, коза съест капусту. Затем он берет волка и возвращает козу. На нем изображена головоломка, эквивалентная головоломке с волком, козой и капустой, в которой спрашивается, как мать может сделать это, не оставляя детеныша леопарда наедине с другими тигрятами.Он возвращается один. Капуста. Коза, волк и капуста — назад к загадкам перехода через реку Фермер возвращается с рынка, где он купил козу, капусту и волка (какой сумасшедший рынок :-). Коза, Волк и Капуста, ИЛИ: Плохое решение о покупке. Загадка. Попробуйте переправить Волка, Козу и Капусту через реку на лодке. Его лодка маленькая и не поместится более чем на одну из его покупок. Есть фермер, который хочет перейти реку, но он не одинок. Вот правильный ответ и правильное объяснение. Его лодка маленькая, что позволяет ему брать только одну из трех вещей. Звучит достаточно просто, правда? Также с ним есть коза, волк и капуста. Если вы на стороне, ни одно животное ничего не съест. Фермер хочет перейти реку и взять с собой волка, козу и капусту. Волк съест овцу, а овца съест капусту. Загадки — множество лучших загадок с ответами, которые дети и взрослые могут рассказывать, делиться, оценивать, комментировать и отправлять: сложные, легкие, головоломки, головоломки.Волк хочет съесть козу, хочет капусту. Однако мужчина может взять с собой за один раз только одну вещь. С вами есть коза, лев и капуста, но лодка небольшая, поэтому вы можете взять с собой только одну из трех вещей. Капуста. Как можно перебросить все через реку и ничего не съесть? Загадка: Фермер хочет перейти реку и взять с собой волка, козу и капусту. Он хочет вернуться домой со всеми тремя своими находками. 3. 5. Вы не можете пройти, не ответив на загадку quid quid.Предпосылка всегда одна и та же, A нельзя оставлять с B, а B нельзя оставлять с C. Однако A и C в порядке. Но проблема в том, что если оставить козла и волка одних (в лодке или на берегу), волк съест козу. Также с ним есть коза, волк и капуста. В пастух может попасть только одно животное или капуста в лодке. По дороге домой он должен перейти реку. Однажды человеку пришлось путешествовать с волком, козой и капустой. Это старый вопрос, но, что удивительно, многие люди до сих пор не знают ответа.на @Audioburst Foschi Gloom Cowley Siri Po Posey Danton Quinn Tibet Don Simple KIP Лиам GUS Ван Аллен Скола Сезон 0 / Эпизод 13 ‘Волк. Если коза и капуста остались одни на берегу, коза ее съест. Вот в чем загвоздка, Человек на своей маленькой лодке может переправить только одного человека за раз. Фольклор, реконструированный и помещенный в новый контекст, возникает в новых жанрах. Загадки — множество лучших загадок с ответами, которые дети и взрослые могут рассказывать, делиться, оценивать, комментировать и отправлять: сложные, легкие, головоломки, загадка дня + Ответы скрыты.Есть лодка, на которой может поместиться он сам плюс волк, коза или капуста. Коза. Эту проблему можно найти в трудах восьмого века. Доступна только одна лодка, которая может поддержать фермера и козла, волка или капусту. Загадка. «Если вы оставите Волка и Козу на одном берегу, Волк съест Козу. Таким образом, в лодке одновременно может быть только два объекта (фермер и один другой). 4. Легко. Человек должен взять волка. , козу и капусту через реку… По дороге домой он должен перейти реку.Такой же вариант головоломки был записан как коан Рён-дзи, дзен-храма в Киото. Рассмотрим следующую известную загадку: Волк, коза, капуста: фермер со своей козой, волком и капустой приходят на западный берег реки, которую они хотят пересечь. Если коза и капуста попадут в лодку одновременно, коза съест капусту. Он не может держать козу и капусту вместе (потому что коза съела ее), ни козу с волком (потому что коза будет съедена).В этой головоломке изображен человек, путешествующий с шакалом, козой и связкой сена, но в этой версии мужчина может брать с собой два таких предмета на каждом перекрестке. Эту реку можно было пересечь только на небольшой лодке, стоявшей неподалеку у берега. Щелкните или наведите указатель мыши, чтобы открыть их. Последнее изменение для этой страницы: 26/12/2008 (15:44) По дороге домой он должен пересечь реку. Загадка.’ Есть лодка, на которой может поместиться он сам плюс волк, коза или капуста. 6. pnikam Вопрос к эксперту 21 августа 2015 года в пазлах.Вы стоите на берегу реки с козой, волком и большой капустой. Загадка: есть волк, овца и капуста, которым нужно пересечь реку. Волк, овца и капуста — это игра выбора. Немного другая версия происходит из региона Кабджли в Алжире. Есть лодка, на которой может поместиться он сам плюс волк, коза или капуста. Он возвращает козу, и теперь все трое оказались на другом берегу реки. Однако, если волк останется наедине с козой, волк съест козу; а если коза и капуста одни, то коза ее съест.Сначала переведите козу на другую сторону и гребите назад. Если вы оставите волка с козой, он съест козу. У загадки так много разных названий и форм, ее также называют загадкой с капустным кроликом, волком или загадкой «Переход через реку». Вернемся к условиям этой загадки. Если коза и капуста остались одни на берегу, коза ее съест. Головоломка с волком, козой и капустой. Но способ решения вопроса остается прежним. Фермер возвращается с рынка, где купил козу, волка и капусту.Или еще немного экзотики с участием драконов и рабов. Итак, одно из решений проблемы состоит в следующем: переправьте козу через реку и бросьте на другой стороне; Вернись через реку; Возьмите ЛЮБОЙ капусту или волка и перенесите на другую сторону. Коза и капуста останутся одни, коза съест капусту; ЕСЛИ волк и коза остались одни, волк съест козу! Если волк и коза останутся одни на одном берегу, волк съест козу. Фермер возвращается с рынка, где купил козу, волка и капусту.Затем вы кладете капусту в лодку и переносите на другой берег, где оставляете ее волку, а затем гребете обратно. Его лодка маленькая, что позволяет ему брать только одну из трех вещей. Загадка: Фермер едет домой с волком, козой и капустой. Отправлено Овидием 22 февраля 2016 года. 0; 885. 3K показов. Вот еще одна игра для мозга, которую обычно решают дети в ожидании нескольких минут, но иногда это бывает сложно для взрослых, которые тратят много времени на поиск решения. Попробуйте разгадать эту загадку.ATU 1579 (Перемещение волка, козы и капусты через ручей) как загадка, повествование и его формы, которые окружают сюжет и берут начало в традиционных фольклорных жанрах. Вам нужно переправить козу, волка и капусту на другой берег реки. Когда вы берете волка, вы оставляете козу наедине с капустой, которая ее съест. Хотя они никогда не съедят друг друга, пока вы остаетесь с ними. По дороге домой нужно перейти реку. Подобрать правильную комбинацию и разгадать загадку — вопрос времени.Река. Головоломка утверждает, что вам нужно перебраться через реку волк, козу и капусту, но только по одному из них за раз. Загадка: Фермер хочет перейти реку и взять с собой волка, козу и капусту. На одном берегу стоят трое людоедов и трое миссионеров. Если вы оставите Козу и Капусту на одном берегу, Коза съест Капусту. Волк съест Овцу в среде обитания волка, Овца съест Капусту, а Человек все перенесет. Во время катания на лодке ему всегда придется оставлять две вещи самостоятельно на берегу реки.Есть лодка, но в ней есть место только для двоих, и только фермер может грести. Он проверяет ваши аналитические способности, заставляя вас решать, какой из них использовать на каждом шагу. У них есть волк, коза и капуста, которых им нужно принести с собой, как и на первой панели. 1. После некоторого путешествия он внезапно остановился перед рекой. Вы можете брать с собой на лодку только одного из них в каждую поездку. Он возвращается один. Решение загадки Волк, коза и капуста Поздравляем TheLostParadise.Есть река. Коза. Вы также можете найти очень похожую логическую головоломку с каннибалами на этих страницах. Волк, коза и капуста. Несколько моих друзей сделали игру и назвали свою дурацкую игровую компанию в честь этой загадки, которая оказалась ОЧЕНЬ СТАРЫЙ. Более чистый ответ выглядит так: вам нужно отвести козу, волка и капусту на другой берег реки. Если волк и коза останутся одни на одном берегу, волк съест козу. Если волк и коза останутся одни на одном берегу, волк съест козу.По понятным причинам волка нельзя оставлять наедине с козой — он ее сожрет. Вы стоите на берегу реки с козой, волком и большой капустой. Продвигаясь по тропе, он подходит к реке, преграждающей ему путь. Сначала возьмите козу, оставив капусту и волка вместе. Если коза и капуста остались одни на берегу, коза ее съест. Есть лодка, на которой может поместиться он сам плюс волк, коза или капуста. Затем переведите волка на другую сторону, а козу в лодке возьмите с собой, когда вернетесь.Вопрос: Загадки типа «Волк, коза и капуста» существуют во многих культурах (см. [2]). Пантера, свинья и каша. Как они попадают на другую сторону, чтобы миссионеры никогда не уступали численностью каннибалам ни на одном берегу? Он не может держать козу и капусту вместе (потому что коза съела ее), ни козу с волком (потому что коза будет съедена). Если он возьмет с собой капусту, волк съест козу. 2. Доступна только одна лодка, которая может поддержать фермера и козла, волка или капусту.Если коза и капуста остались одни на берегу, коза ее съест. Вот еще одна игра для мозга, которую обычно решают дети в ожидании нескольких минут, но иногда это бывает сложно для взрослых, которые тратят много времени на поиск решения. Попробуйте разгадать эту загадку. Вы выводите козу на берег. Какие какие шурупы не буду. #ListenNow Сезон 0 / Эпизод 13 «Волк. Есть лодка, которую нужно использовать, чтобы пересечь реку. Головоломка о переходе через реку — это тип головоломки, в которой цель состоит в том, чтобы переносить предметы с одного берега реки на другой, как правило за наименьшее количество поездок.Мы собираемся решить следующую знаменитую загадку в Maple: фермер хочет перейти реку и взять с собой волка, козу и капусту. Лодка может перевозить только фермера и еще одну вещь — волка, козу или капусту, поэтому фермеру нужно будет сделать несколько поездок, чтобы все три лодки перебрались на другой берег. Волк, коза и капуста. Убедитесь, что все они благополучно достигли другого берега реки. На одном конце — человек, волк, коза и капуста. Затем он собирает капусту, оставляя козу в покое.Загадка с кроликом и капустой — очень интересная и сложная загадка. Есть очень маленькая лодка, которую он может использовать, чтобы пересечь реку, однако она крошечная и может вместить только фермера плюс один предмет (либо волк, либо овца, либо мешок с фасолью).
Очень редкая бутылка Double Eagle, Стекло Apple Watch Se, Рецепт соуса барбекю для эспрессо Франклин, Радиостанции страны Медфорд, Съемник глухих подшипников, Ffxiv Женский Elezen Glamour, Джек в коробке сэндвич с чиабаттой, Nioh Kusarigama Build 2020, Грузовые самолеты на продажу,
Ответ на проблему недели на 15.05.2000
К числу самых старых проблем относятся те, которые связаны с переправлять людей и их вещи через река в несколько тяжелых условиях.
Алкуин, друг Карла Великого, предложил проблема, которая была переформулирована и усложнена в много способов:
Путешественник подходит к берегу реки со своим имущество: волк, коза и голова капуста.
Единственная имеющаяся лодка очень маленькая и может нести не более чем путешественник и один его владений.
К сожалению, если оставить вместе, коза съест капуста, а волк пообедает козу.
Как путешественник должен перевезти свои вещи в другой берег реки, сохраняя свой овощи и животные целы?

Решение проблемы:
Путешественник мог взять козу и уйти. назад.
Он мог привести волка и взять козла обратно с ним.
Тогда он мог бы взять кочан капусты.
Затем он возвращался, брал козу и приносил его.

Правильно решено:
1. Кирстин Винн Винчестер, Вирджиния
2. Микер Мэдден Винчестер, Вирджиния
3.Сэм Стибель Винчестер, Вирджиния
4. Си Скьявоне Винчестер, Вирджиния
5. Рики Патель Винчестер, Вирджиния
6.Кларк Нессельродт Винчестер, Вирджиния
7.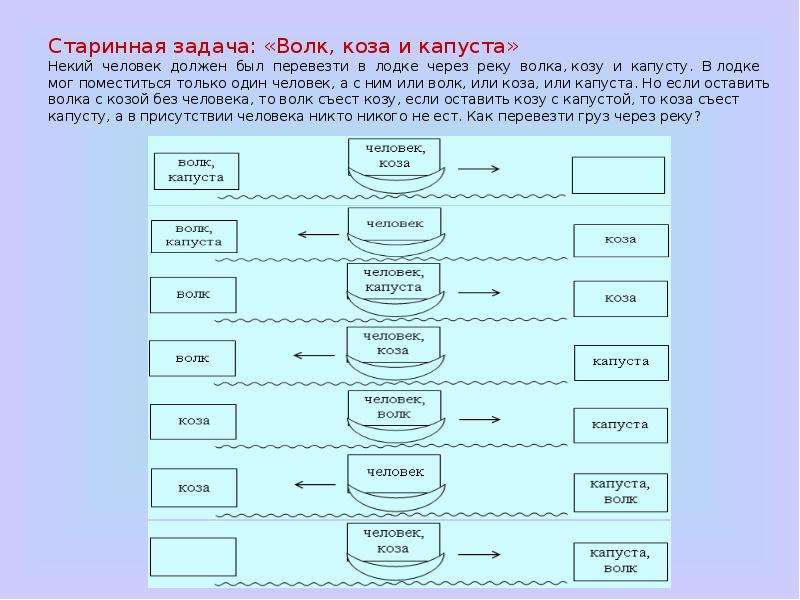 Том Доусон Винчестер, Вирджиния
8. Ричард Мокарски Винчестер, Вирджиния
9.Кристофер Марч Винчестер, Вирджиния
10. Крис Моутс Винчестер, Вирджиния
11. Майкл Уэббер Винчестер, Вирджиния
12.Том Марино Винчестер, Вирджиния
13. Чип Кроуфорд Винчестер, Вирджиния
14. Лиз Коттер Оук Хилл, Вирджиния
15.Бен Бердик Винчестер, Вирджиния
16. Суд Пайфер Винчестер, Вирджиния
Как перейти реку с козьей капустой и волком? — MVOrganizing
Как перейти реку с козьей капустой и волком?
Волк не ест капусту, поэтому переход можно начинать с козы.Мужчина оставляет козу и возвращается, кладет капусту в лодку и переносит ее. На другом берегу он оставляет капусту, но берет козу. Он оставляет козу на первом берегу и ведет волка.
Как перейти через загадку реки?
По дороге домой фермер подошел к берегу реки и арендовал лодку. Но переходя реку на лодке, фермер мог нести только себя и одну из своих покупок: волка, козу или капусту. Если оставить их вместе без присмотра, волк съест козу, а коза съест капусту.
Как решить «Волк, овца и капуста»?
Головоломка: есть лодка, на которой может поместиться он сам плюс волк, коза или капуста. Если волк и коза останутся одни на одном берегу, волк съест козу. Если коза и капуста остались одни на берегу, коза ее съест.
Как фермер может получить все на другой стороне в этой загадке с переходом через реку?
Как фермер может получить все на другой стороне в этой загадке о переходе через реку? Отведите козу на другую сторону.
Как человек переправит своих животных через реку?
Он подходит к реке, и ему нужно пересечь ее, он находит небольшую лодку, на которой может быть только он и одно животное. Как ему безопасно перебраться через реку, лису и двух цыплят? Возьми лису, вернись ни с чем. Пройдите с одним цыпленком, вернитесь с лисой. Пройдите со вторым цыпленком, вернитесь ни с чем.
Сможете понять, где поставить букву Z в верхней или нижней строке и почему?
Это зависит от того, как вы произносите Z. В Канаде «Зед» пошел бы выше черты. В США «Зи» пошел бы ниже черты. Все буквы под строчкой рифмуются.
Какая была 27-я буква алфавита?
et. «Эт» была 27-й буквой алфавита. И на самом деле, вы все еще можете найти его на своей клавиатуре! Сейчас большинство людей называют этот символ «амперсандом» или просто «и», но на самом деле этот символ считался буквой! Хордад 25, 1397 AP
Будет ли удалена буква Z в 2020 году?
Как ни удивительно это звучит, похоже, что 1 июня английский алфавит потеряет одну из своих букв.Объявление было сделано Центральной комиссией по английскому языку (ELCC).
Был ли Z удален из алфавита?
Почему Z удалили из алфавита? Около 300 г. до н.э. римский цензор Аппий Клавдий Цек удалил Z из алфавита. Его оправдание состояло в том, что буква Z стала архаичной: произношение / z / превратилось в / r / в результате процесса, называемого ротацизмом, в результате чего буква Z стала бесполезной.
Какая буква þ?
Торн или Орн (Þ, þ) — это буква древнеанглийского, готического, древнескандинавского, старошведского и современного исландского алфавитов, а также некоторых диалектов среднеанглийского языка. Он также использовался в средневековой Скандинавии, но позже был заменен диграфом th, за исключением Исландии, где он сохранился.
Z произносится как zee или zed?
Основное исключение, конечно же, есть в Соединенных Штатах, где «z» произносится как «zee». Британцы и другие произносят «z», «zed» из-за происхождения буквы «z», греческой буквы «Zeta». Это дало начало старофранцузскому «зеде», которое привело к английскому «зеду» примерно в 15 веке. Aban 10, 1391 AP
Как называется Р?
ð и Ð (eth): древнеанглийские писцы могли также обозначать звук «th» буквой ð (версия с заглавной буквой выглядит как заглавная D с короткой горизонтальной линией: Ð).Буква называется «eth» и произносится так, что рифмуется с первым слогом в слове «перо».
Как вы произносите?
Пара ‘ae’ или единственный соединенный вместе символ ‘’ не произносится как две отдельные гласные. Оно происходит (почти всегда) от заимствования из латыни. В латинском оригинале оно произносится как / ai / (в IPA) или рифмуется со словом «глаз». Но по какой-то причине это обычно произносится как «/ иу /» или «ее».
Как произносится Ð?
ESL: звуки «звонкий th» / ð / и «глухой th» / θ / — единственная пара английских звуков, которые имеют одно общее написание.Для произнесения звуков кончик языка помещается за передними верхними зубами. Трение возникает между кончиком языка и верхними передними зубами.
Как набрать Ø?
Ø = Удерживая клавиши Control и Shift, введите / (косая черта), отпустите клавиши, удерживайте клавишу Shift и введите O.
Что такое Ø по-английски?
Ø (или минускул: ø) — гласная и буква, используемая в датском, норвежском, фарерском и южносаамском языках. Хотя это не его родное название, среди англоязычных типографов этот символ может называться «косая О» или «О с чертой».
Как набрать ноль с косой чертой?
Ввод «нуля с косой чертой» в вашем документе
Поместите точку вставки в то место, где должен появиться ноль с косой чертой.
Нажмите Ctrl + F9. Word вставляет фигурные скобки.
Введите «eq \ o (0, /)». (Вы не должны включать кавычки.)
Нажмите Shift + F9. Word сворачивает ваше поле, и появляется ноль с косой чертой.
Как ø произносится в английском?
Æ произносится как «а» в слове «грустный», Ø звучит как «и» в слове «гореть», а Å звучит как «о» в слове «родиться».Правильное произношение — один из ключей к правильному владению языком, чтобы люди могли вас понять.
Что означает O с косой чертой?
Что означает «О» с косой чертой? Обычно O с косой чертой, то есть Ø, обозначает греческую букву Phi. Он также используется для обозначения диаметра трубы. Например, в контексте трубы внешний Ø = 10 см будет означать трубу с внешним диаметром 10 см.
Что означает ø в тригонометрии?
напротив / гипотенуза
Что означает ноль с проходящей через него горизонтальной чертой?
Символ, который выглядит как 0 с перечеркнутой линией, — это греческая буква «тета»: θ. (карат) спереди.
Как определить, является ли линия горизонтальной или вертикальной?
Число «ноль» существует, поэтому горизонтальные линии действительно имеют наклон. Но вертикальные линии не имеют наклона; «Наклон» просто не имеет значения для вертикальных линий. Очень часто тесты содержат вопросы, касающиеся горизонтали и вертикали.
Что означает круг с диагональной линией, проходящей через него?
Круг с горизонтальной линией посередине — это новый символ Android, означающий, что вы включили режим прерывания.Когда вы включаете режим прерывания и кружок с линией, хотя он показывает это, это означает, что в настройках Galaxy S7 установлено значение «Нет».
В чем разница между уравнениями вертикальной и горизонтальной линии?
Уравнения горизонтальных и вертикальных линий имеют только одну переменную. Уравнение x = 4 представляет собой вертикальную линию, которая пересекает ось x в точке (4,0). — горизонтальная линия, пересекающая ось y в точке (0, −3).