Правила игры сапер на компьютере: Как играть в Сапера
Как играть в Сапёра: правила и рекорды игры
Стандартная игра «Сапёр» в Windows«Сапер» – несложная игра, которая, тем не менее, развивает внимание, память и логику. Основная ее цель — найти и обозначить флажками мины. Нужно быть очень осторожным: как только вы открываете на клетку, под которой спрятан взрывоопасный сюрприз, игра окончена. Сапер ошибается только один раз.
Начнем с того, где найти игру «Сапер». Нажимаете кнопку «Пуск», в открывшемся меню находите сроку «Игры», активируете ее.
Где найти игру «Сапер»В появившемся перечне игр находите «Сапер», два раз кликаете левой клавишей мышки по значку.
Запускаем игру «Сапер»Игра запущена. Она имеет три уровня сложности: новичок, любитель и профессионал. Изменить сложность можно зайдя в меню «Игра» и выбрав там строку «Параметры», или просто нажав функциональную клавишу на клавиатуре F5. Выбираете тот уровень сложности, который вам больше нравится, или который вам по силам.
Параметры «Сапера»Открывается игровое поле. Под некоторыми клетками спрятаны «мины». Основная задача – вычислить их и не «подорваться». Количество не найденных мин отображено в нижнем левом углу.
Под некоторыми клетками спрятаны «мины». Основная задача – вычислить их и не «подорваться». Количество не найденных мин отображено в нижнем левом углу.
Чтобы начать игру нужно щелкнуть в произвольном месте на поле (главная задача тут – не нарваться сразу на мину). Откроется некоторый участок поля, на котором появятся цифры. Все эти цифры служат для облегчения поиска установленной мины.
Начало игрыЦифра «1» означает, что в расположенных вокруг нее ячейках, находится одна мина. Если оказывается открытой единственная ячейка, значит, под ней она и скрыта. Чтобы случайно на нее не нажать, щелкните по ней правой клавишей мышки. На этой клетке появится флажок, а счетчик сюрпризов, которые нужно найти, уменьшится.
Чтобы отменить выделение дважды щелкните правой клавишей мышки. Флажок сначала сменится на знак вопроса (можете его оставить, если не уверены, есть там взрывоопасный сюрприз или нет), а после второго «клика» исчезнет.
Вычисляя все возможные места нахождения мин, вы понемногу открываете карту. Внимательно смотрите и находите взрывоопасные сюрпризы: как только попадете на занятую миной клетку, игра окончена.
Внимательно смотрите и находите взрывоопасные сюрпризы: как только попадете на занятую миной клетку, игра окончена.
Каждый вырабатывает свою тактику. Для меня удобнее сразу открыть все мины, которые находятся на «выступающих» клетках. Если посмотрите на фото, поймете, о чем я. В таких местах можно действовать особо не раздумывая. Вариантов нет. Мины именно там.
Мины именно тамБыстренько расставляем флажки (щелчок павой клавишей мышки по клетке).
Расставляем флажки на минахА вот дальше пошла потеха: предстоит проверять остальные клетки. Для удобства я очертила расположенные рядом области разными цветами.
Вычисляем миныВосемь клеток вокруг цифры «1» (обозначены розовым цветом) содержат только одну мину. Смело ставим тут флажок (у меня он уже стоит — поставила, когда отмечала все «выступы»). Рядом с флажком остались две не открытые клетки. Их можно открывать, так как мина в окружающих клетках уже найдена. Под остальными взрывоопасных сюрпризов нет.
Вычисляем миныНиже имеется цифра «2» (зеленый цвет). Это значит, что 8 клеток вокруг нее содержат 2 мины. Обе уже обнаружены и не открытых клеток нет. Если теперь рассмотреть «2» расположенные выше и ниже (отмечены белым цветом), то увидим, что в окружающих клетках невозможно вычислить, где спрятаны мины. Потому лучше не рисковать, и перейти их искать в другом месте.
Это значит, что 8 клеток вокруг нее содержат 2 мины. Обе уже обнаружены и не открытых клеток нет. Если теперь рассмотреть «2» расположенные выше и ниже (отмечены белым цветом), то увидим, что в окружающих клетках невозможно вычислить, где спрятаны мины. Потому лучше не рисковать, и перейти их искать в другом месте.
Таким вот способом находите все мины, расположенные на поле. Если не знаете, куда ставить флажок, переходите на другой кусок карты. Возможно, получится подобраться к этому участку с другой стороны. Ничего особенно сложного нет, но требуется внимательность и известная доля логики.
Обратите внимание, что игрок расставляет не все флажки, а только часть. По всей видимости он выставляет флажки там, где можно запутаться и ошибиться. Там где «и так все понятно», игрок, для экономии времени, флажки не ставит. Некоторые игроки, вообще обходятся без выставления флажков — тут у каждого свои трюки и секреты.
Там где «и так все понятно», игрок, для экономии времени, флажки не ставит. Некоторые игроки, вообще обходятся без выставления флажков — тут у каждого свои трюки и секреты.
Продвинутая тактика игры в «Сапёр» / Хабр
[Пятничный перевод статьи 1999 года одного из авторов движка игры Thief Шона Барретта]
Неприятное положение в «Сапёре»
В этом положении я знаю, что вокруг меня есть куча мин, но не могу определить, где они находятся. Несколько мин может быть в одном из двух мест (розовые или голубые), группа мин может быть расположена в одной из двух комбинаций (светло-/тёмно-зелёные). Кроме того, есть ещё сложная ситуация с «5» и «6» в левом верхнем углу, которую я никак не выделил.
Голубые/розовые — взаимоисключающие пары, светло-/тёмно-зелёные — взаимоисключающие группы
«Сапёр»: логика или вероятность
В «Сапёра» можно играть двумя способами: как в логическую или в вероятностную игру.
Технически, вероятность подразумевает логику. Если вы можете логически доказать, что мина должна находиться в определённом месте, то вероятность равна 100%. Если можете доказать, что её в этом месте нет, то вероятность равна 0%. То есть в каком-то смысле для нас важны только вероятности. Тем не менее, игрок для распознавания таких стопроцентных ситуаций игрок использует логическую дедукцию. Иногда, особенно на низких уровнях сложности, её достаточно для прохождения уровня, никакого подсчёта вероятностей не требуется.
Но бывают такие ситуации, когда вся логика мира не может вас спасти. Простой пример — ситуация с «T», которую видно внизу по центру. Она немного осложняется дополнительными соседними минами. (В простейшем случае «2» заменяется на «1», а «5» — на «3», чтобы ситуация была симметричной.)
Нет никакого способа получить больше информации о вероятном положении одной мины, оставшейся в одной из этих клеток. Шансы пятьдесят на пятьдесят — можете бросать монетку. Когда у вас получается что-то подобное, лучше сразу же сделать выбор и не откладывать на потом. Если догадка будет неверной, то вы хотя бы сэкономите время на решение остальной части поля. (Но лично я стремлюсь к завершённости, поэтому оставляю такие случаи на потом. И не вините себя за то, что не угадали. Когда победа или проигрыш зависят от броска монеты — это плохой гейм-дизайн.)
Когда у вас получается что-то подобное, лучше сразу же сделать выбор и не откладывать на потом. Если догадка будет неверной, то вы хотя бы сэкономите время на решение остальной части поля. (Но лично я стремлюсь к завершённости, поэтому оставляю такие случаи на потом. И не вините себя за то, что не угадали. Когда победа или проигрыш зависят от броска монеты — это плохой гейм-дизайн.)
Тактика в конце игры
В эндшпиле можно использовать очень простую тактику — считать количество оставшихся мин. Допустим, я решил всё, кроме правой нижней части поля. Здесь может быть всего две конфигурации мин, соответствующих данным:
Возможные конфигурации мин в правом нижнем углу
Если у вас получилась такая позиция и счётчик говорит, что осталось всего две мины, то ответ готов: это должна быть конфигурация B.
Если счётчик говорит, что осталось три мины, то это необязательно конфигурация A.
На самом деле, шансы в пользу конфигурации B.
Локальные вероятности
Если вы исследуете вероятности только «локально», вы видите, что каждая из клеток в отмеченных взаимоисключающих группах имеет шанс 50-50 быть миной. Говоря «локально», я подразумеваю, что если рядом с двумя неизвестными клетками есть «1», то вероятность спрятанной мины у каждой из них равна 50%.
Именно такая ситуация сложилась внизу в центре: каждая из соседних клеток, соседних к неизвестной паре, содержит в точности одну мину, то есть каждый из соседних фрагментов данных предполагает 50-процентную вероятность. В самом левом верхнем углу похожая ситуация:
С абсолютной точностью в каждом из розовых овалов есть по одной мине, то есть всего осталось 7 мин
Ситуация в правом нижнем углу тоже чем-то похожа: рядом с каждым из чисел на «границе» есть одна мина и две клетки, в которых она может быть.
Если рядом с клеткой есть одна скрытая мина, но три закрытых клетки, то вероятность мины в каждой из клеток составляет 33%; каждая из четырёх закрытых клеток имеет вероятность 25%. Если у нас две скрытые мины и три закрытых клетки, то каждая клетка имеет вероятность 66%.
Вот ситуация с «локальной вероятностью» для всего поля:
Как вы видите, несколько клеток в верхней левой области имеют несколько вероятностей; закрытая клетка рядом с «2» и «6» и одна рядом с «3» и «5». (Клетка рядом с «5» и «6» благодаря им всё равно имеет вероятность 66%, поэтому нет видимого несоответствия.)
Разрешение конфликтов локальной вероятности
Вы наверно, задаётесь вопросом, что значит наличие конфликтующих локальных вероятностей. Интуиция может подсказать, что наибольшая вероятность должна выиграть. Например, клетка между «6» и «2» должна на самом деле иметь 66%. Это будет значить, что у крайней левой клетки с вероятностью 50% она на самом деле равна 33%.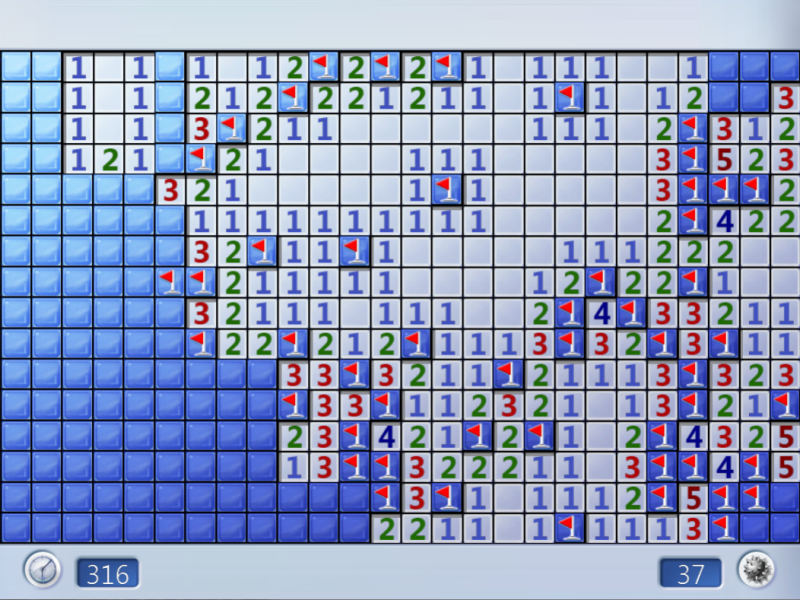
Но ничто из этого на самом деле неверно. Данные, из которых получены вероятности, не независимы друг от друга, поэтому никакие прямолинейные математические расчёты не будут верными. Причина правильности локальной догадки о 50% внизу в центре в том, что она действительно независима ни от чего другого. Если случайным образом воссоздавать поле по уже имеющимся у нас данным, то ровно в половине из моделей мина будет в одной из двух клеток. (Вероятность иногда запутывает людей, которые не могут разобраться, какие правила расчёта вероятностей применимы в конкретной ситуации. Такой подход — это гарантировано верный путь, потому что он основан на определении вероятности в статистическом прогнозировании: вычисление выполняется измерением во всех возможных конфигурациях, которые могли привести к текущей ситуации, при этом все они считаются одинаково вероятными.)
То есть для верных измерений в ситуации в левом верхнем углу нужно рассмотреть все возможные конфигурации мин, удовлетворяющие уже собранным данным, а затем посчитать, какой процент из них содержит мину в нужной позиции.
Непосредственный подсчёт потребовал бы много времени. К счастью, существуют и другие способы.
Подсчёт конфигураций
Абстрактный способ вычисления вероятностей заключается в обходе всех возможных конфигураций мин, отбрасывании конфигураций, не отвечающих собранным данным, и вычислении статистики для каждой из возможных позиций.
Более практичный подход — рассматривать только те варианты, которые нельзя отбросить. Для этого нам нужно применить логику и сгенерировать все возможные ситуации, которые могут соответствовать имеющимся данным. Я уже показывал два варианта для правого нижнего угла, а вот вероятности для левого верхнего:
Возможные конфигурации для левого верхнего угла
(Как и раньше, овал высотой в две клетки показывает, что мина может с одинаковой вероятностью находиться в любой из клеток. Я мог бы перечислить каждый из двух этих случаев отдельно, то есть получилось бы 10 конфигураций, но никакой пользы в этом для нас нет. Структура таблицы: два ряда (пронумерованные как «1» и «2») отличаются положением мины в четвёртом ряду. Три столбца характеризуются положением мин во втором ряду.)
Структура таблицы: два ряда (пронумерованные как «1» и «2») отличаются положением мины в четвёртом ряду. Три столбца характеризуются положением мин во втором ряду.)
Теперь есть искушение воскликнуть: «ага, вот пять случаев, так что мы можем подсчитать количество случаев для каждой из возможных позиций мины». Например, мина находится в четвёртом ряду (рядом с левой нижней «1») находится слева в двух верхних случаях, и справа в трёх нижних случаях. Поэтому можно решить, что она имеет вероятность в 60% находиться справа, рядом с «6». (Это позиция с конфликтующими локальными вероятностями 50% и 66%.)
Однако мы упускаем одну тонкость — количество мин в некоторых случаях разное: в A1 шесть мин, в B2 — четыре, и по пять во всех остальных случаях.
Считаем ненайденные мины
Для подробного изучения этой тонкости давайте вернёмся к более простой ситуации в правом нижнем углу.
Возможные конфигурации с правом нижнем углу
Предположим, что я уже открыл остальное поле и знаю, что осталось ровно три мины.
Есть искушение предположить, что наиболее вероятна конфигурация A ровно с тремя минами. Но это неверно.
Ещё одно искушение — вспомнить, сколько всего было мин и сколько всего клеток, и сказать: «каковы шансы того, что нижняя область 3×3 будет пустой». Это тоже неверно. Очень сложно объяснить, почему это ошибка, наверно, её можно сравнить с парадоксом Монти Холла. Однако достаточно сказать, что в действительности шансы в этой ситуации не зависят от общего количества мин и размера поля.
Правильный ответ таков: сколько возможных конфигураций из трёх мин соответствуют нашим знаниям о поле? Из рисунка мы видим, что две: конфигурации A и B. Но в B всего две мины. Третья мина может быть в любой из клеток нижней области 3×3, о которой мы пока не собрали никаких данных. То есть всего есть девять вариантов конфигураций B, я просто не стал изображать их все.
Следовательно, существует всего десять возможных конфигураций. Каждая из десяти конфигураций равновероятна.
Поскольку каждая из десяти конфигураций (девять для B, одна для A) равновероятны, конфигурация B в данном случае имеет вероятность 90%!
Если бы на этом этапе было четыре мины, то у конфигурации A имелось бы девять вариантов. Конфигурация B имела бы по одному варианту для каждого варианта расположения двух мин в левом нижнем углу; это C(9,2), то есть 9!/((9-2)! * 2!) или 9*8/2, равное 36. В этом случае конфигурация B имела бы вероятность только 75%.
В этом случае конфигурация B имела бы вероятность только 75%.
С пятью минами конфигурация A имела бы 36 вариантов, а конфигурация B — 9*8*7/6 = 84 варианта; то есть шансы B были бы чуть больше 66%.
В случае шести мин B имела бы вероятность 60%. С семью минами у B было бы всего 50%. С восемью минами B была бы менее вероятна, чем A; в этом случае с таким количеством мин в оставшихся позициях конфигураций становится меньше. Рассмотрим наихудший случай, когда осталось 11 мин. (Шанс этого чрезвычайно мал, но если такая ситуация возникнет, то применимы эти вероятности.) В конфигурации B, во всех закрытых клетках будут мины, в конфигурации A во всех, кроме одной. То есть существует 9 вариантов для A и всего один для B.
Окончательное решение
На имеющемся у нас поле осталось девять мин. Одна из них находится в центральной нижней области, и её положение полностью независимо, поэтому можно его игнорировать. То есть мы рассматриваем всё поле, кроме этого случая: не найдено всего восемь мин. (Чтобы не возникло путаницы, я продолжу явным образом считать овал в левом верхнем углу, потому что это изображение левого верхнего угла.)
То есть мы рассматриваем всё поле, кроме этого случая: не найдено всего восемь мин. (Чтобы не возникло путаницы, я продолжу явным образом считать овал в левом верхнем углу, потому что это изображение левого верхнего угла.)
Может сложиться любая комбинация из левой верхней и правой нижней конфигураций, за исключением одной из них (A1 + A), для которой потребуется девять мин. Поэтому мы должны перечислить каждую из этих возможных конфигураций и сосчитать оставшиеся мины и закрытые клетки.
На самом деле, количество закрытых клеток независимо: их девять в правом нижнем углу и три в левом верхнем, то есть всего 12.
| Вверху слева | Внизу справа | Количество мин | Осталось мин | Закрытые варианты |
|---|---|---|---|---|
| A1 | B | 8 | 0 | 1 |
| B1 | A | 8 | 0 | 1 |
| B1 | B | 7 | 1 | 12 |
| A2 | A | 8 | 0 | 1 |
| A2 | B | 7 | 1 | 12 |
| B2 | A | 7 | 1 | 12 |
| B2 | B | 6 | 2 | 66 |
| C2 | A | 8 | 0 | 1 |
| C2 | B | 7 | 1 | 12 |
Таким образом, всего существует 118 возможных комбинаций. Исходя из этого мы можем независимо посчитать количество комбинаций для каждой из левых верхних и правых нижних конфигураций:
Исходя из этого мы можем независимо посчитать количество комбинаций для каждой из левых верхних и правых нижних конфигураций:
| Конфигурация | Варианты | Процент |
|---|---|---|
| A1 | 1 | 1 |
| B1 | 13 | 11 |
| A2 | 13 | 11 |
| B2 | 78 | 66 |
| C2 | 13 | 11 |
| A | 15 | 13 |
| B | 103 | 87 |
Далее я обошёл каждую клетку на поле и вычислил её вероятность, суммировав количество вероятностей, в которых она появляется, и поделив на 118. (На самом деле, просто сложив указанные выше проценты.) Кроме того, в среднем в каждой из закрытых клеток есть мина в 15 из 118 вариантов (то есть шансы на то, что по крайней мере в одной закрытой клетке есть мина, очень высоки). [Это можно вычислить умножением количества оставшихся мин на закрытые варианты, что даёт нам среднее количество мин в закрытых клетках.]
[Это можно вычислить умножением количества оставшихся мин на закрытые варианты, что даёт нам среднее количество мин в закрытых клетках.]
Вероятности наличия мины
(Следует сказать, что это не показывает всей доступной информации. Например, мы знаем, что вероятности двух тёмно-зелёных клеток с 87% связаны — если одна верна, то другая тоже. И голубые 13-процентные клетки, в которых есть мины по конфигурации A, тоже связаны. Остальные голубые 13-процентные клетки не связаны. Если в одной из них есть мина, вероятность того, что в любой из оставшихся есть мина, уменьшаются.)
Играем в игру
Скорее всего, играя в «Сапёра», вы не захотите корпеть над всеми этими вычислениями.
И я тоже.
Но я действительно перечислил все возможные конфигурации в левом верхнем и правом нижнем углах. Я заметил, что в одной конфигурации (B2-B) используется на одну мину меньше, чем во всех остальных, и применил проверенное временем правило «меньше мин — значит, больше закрытых вариантов» (которое действует приблизительно пока количество закрытых клеток меньше чем удвоенное количество ненайденных мин). Это означает, что намного вероятнее конфигурации с меньшим количеством мин.
Это означает, что намного вероятнее конфигурации с меньшим количеством мин.
Поскольку в левом верхнем углу было множество конфигураций, определение шансов для любой клетки довольно сложно. Поэтому я просто выяснил, что конфигурация B в правом нижнем углу намного более вероятна, и случайно выбрал одну из подходящих клеток. (Я надеялся, что она позволит мне закончить правый нижний угол, а потом, вооружённый большей информацией о количестве оставшихся мин, я смогу завершить левый верхний угол, после чего мне придётся бросить монетку для выбора внизу в центре. Разумеется, в идеале нужно было выбрать клетку, максимизирующую вероятность получения полезной информации, но любая из этих догадок позволила бы мне «войти» в правый нижний угол для дальнейшего сбора данных.) Шансы были выше у конфигурации B, поэтому я выбрал клетку, в которой была мина в конфигурации A.
Восемь раз из девяти я был бы прав.
Системные требованияSapper — можно ли запустить?
Sapper Системные требования — полные спецификации, средство проверки системы и необходимые настройки игрового ПК.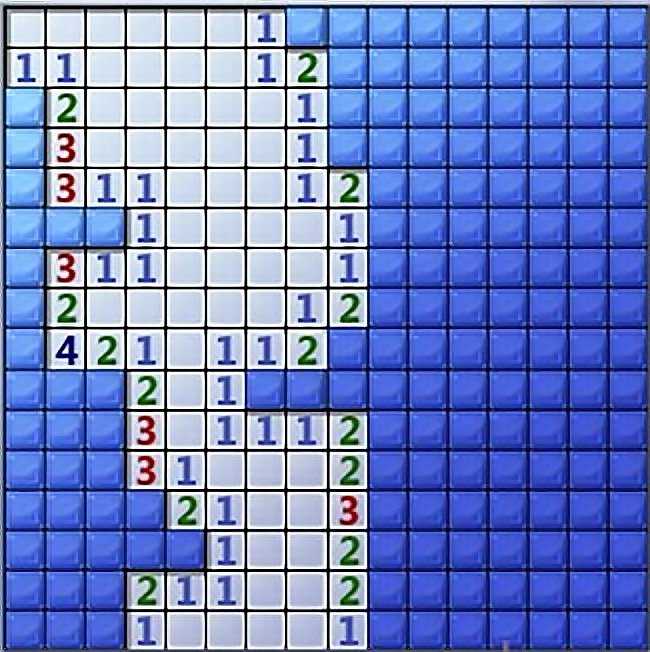
- Память: 4 ГБ
- Видеокарта: ATI Radeon HD 4850
- ЦП: AMD Athlon 64 FX-51
- Размер файла: 261 МБ
- ОС: Windows® 10 64-разрядная
Минимальные саперные требования
- Память: 3 ГБ
- Видеокарта: NVIDIA GeForce 8600 GT
- ЦП: AMD Athlon 64 FX-34
- Размер файла: 261 МБ
- ОС: Windows® 7 / Windows® 8 / Windows® 10
Можешь запустить? Проверьте свой компьютер на соответствие системным требованиям Sapper .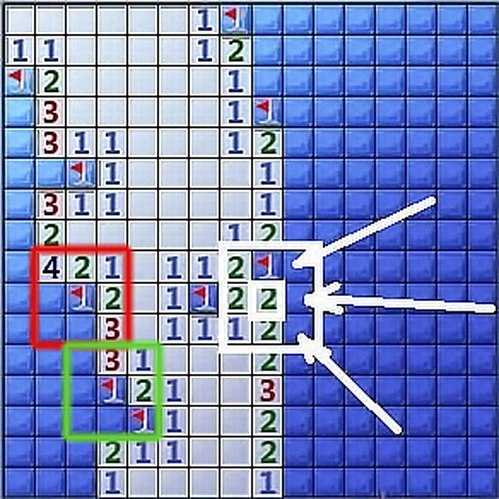
Могу ли я запустить его?
Автоматическое тестирование ПК Могу ли я запустить его?
Введите информацию о вашей системе
Могу ли я запустить Sapper?
В системных требованиях Sapper указано, что вам потребуется не менее 3 ГБ оперативной памяти. Если возможно, убедитесь, что у вас есть 4 ГБ ОЗУ, чтобы использовать Sapper в полной мере. Самая дешевая видеокарта, на которой вы можете играть, — это NVIDIA GeForce 8600 GT. Но, по словам разработчиков, рекомендуемая видеокарта — ATI Radeon HD 4850. Для запуска Sapper требуется как минимум процессор AMD Athlon 64 FX-34. Тем не менее, разработчики рекомендуют ЦП, больший или равный AMD Athlon 64 FX-51, чтобы играть в игру. Для установки Sapper вам потребуется не менее 261 МБ свободного места на диске.
Sapper будет работать на ПК с ОС Windows® 7 / Windows® 8 / Windows® 10 и выше.
Ищете обновление? Воспользуйтесь нашими простыми в использовании руководствами по настройке Sapper , чтобы найти лучшие и самые дешевые карты.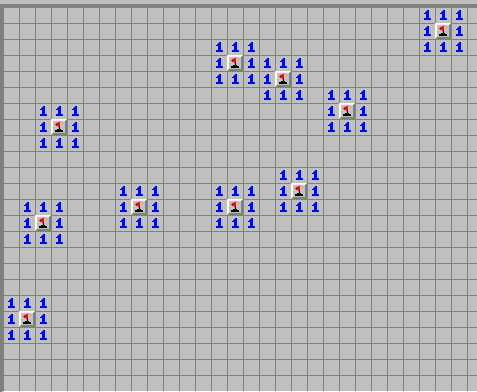 Фильтр для сравнения видеокарт Sapper и сравнения процессоров. Мы поможем вам найти лучшее предложение по правильному оборудованию для запуска игры.
Фильтр для сравнения видеокарт Sapper и сравнения процессоров. Мы поможем вам найти лучшее предложение по правильному оборудованию для запуска игры.
Скачать: | Через Steam |
|---|---|
Разработчики: | Фабрис Руане-Амелен Винсент Хадиге Энтони Рабо |
Издатель: | Рубика Supinfogame |
Категория: | Инди |
| Дата выпуска сапера : | 18 декабря 2019 |
Сапер ПК цена сегодня:
19,99 долларов США
Что такое Сапер?
Игра-головоломка, в которой вы разрушаете замки цепными реакциями огня, обвалов и взрывов.
Ищете готовую систему? У нас в базе данных 1478 ноутбуков, на которых может работать Sapper . Мы принимаем более 808 игровых ноутбуков стоимостью менее 1000 долларов. Ознакомьтесь с нашей полной таблицей сравнения ноутбуков, чтобы найти подходящие системы или лучшие предложения, которые мы выбрали ниже.
Последние сообщения
- Монитор
FPS: как отслеживать частоту кадров в игре на ПК с помощью счетчика FPS
23 августа 2022
класс = «маленький заголовок»>
Системные требования Overwatch 2 Системные требования FIFA 23 Системные требования Call of Duty Modern Warfare 2 Системные требования ГТА 5 Системные требования Cyberpunk 2077 Системные требования Gotham Knights Системные требования Valorant Системные требования Elden Ring Системные требования Red Dead Redemption 2 Системные требования Call of Duty: Warzone Системные требования Fortnite Системные требования Genshin Impact Системные требования Warhammer 40,000: Darktide Системные требования Persona 5 Royal Требования к системе Need for Speed Heat Системные требования Виктории 3 Системные требования Майнкрафт Системные требования Call of Duty: Warzone 2 Системные требования Tower of Fantasy Системные требования The Sims 5Системные требования Sapper — можно ли запустить?
The Sapper Системные требования — полные спецификации, средство проверки системы и необходимые настройки игрового ПК.
- Память: 2 ГБ
- Видеокарта: Intel HD 2000
- ЦП: Intel Pentium 4 2,00 ГГц
- Размер файла: 300 МБ
- ОС: Windows 10
Минимальные требования Sapper
- Память: 512 МБ
- Видеокарта: Intel HD 2000
- ЦП: Intel Pentium 4 2,00 ГГц
- Размер файла: 200 МБ
- ОС: Windows XP
Можешь запустить? Проверьте свой компьютер на соответствие системным требованиям The Sapper .
Могу ли я запустить его?
Автоматическое тестирование ПК Могу ли я запустить его?
Введите информацию о вашей системе
Могу ли я запустить Sapper?
Для запуска The Sapper требуется как минимум процессор Intel Pentium 4 2,00 ГГц. Для установки The Sapper вам потребуется не менее 200 МБ свободного места на диске. Убедитесь, что у вас есть 300 МБ свободного места на диске, чтобы установить The Sapper. Минимальные требования к памяти для The Sapper: 512 МБ оперативной памяти, установленной на вашем компьютере. Если возможно, убедитесь, что у вас есть 2 ГБ ОЗУ, чтобы запустить The Sapper в полной мере. При условии, что у вас есть хотя бы видеокарта Intel HD 2000, вы можете играть в игру.
Sapper будет работать на ПК с Windows XP и выше. Кроме того, у него есть версии для Mac и Linux.
Ищете обновление? Воспользуйтесь нашими простыми в использовании руководствами по настройке The Sapper , чтобы найти лучшие и самые дешевые карты. Фильтр для сравнения видеокарт The Sapper и сравнения процессоров. Мы поможем вам найти лучшее предложение по правильному оборудованию для запуска игры.
Фильтр для сравнения видеокарт The Sapper и сравнения процессоров. Мы поможем вам найти лучшее предложение по правильному оборудованию для запуска игры.
Системные требования Sapper Mac OS (минимальные)
- Память: 512 МБ
- Видеокарта: NVIDIA GeForce GTX 950
- ЦП: Intel Pentium 4 2,00 ГГц
- Размер файла: 200 МБ
- ОС: Mac OS X 10.9+
Системные требования Sapper Linux (минимальные)
- Память: 512 МБ
- Видеокарта: ATI FireMV 2400 PCIe
- ЦП: Intel Core 2 Duo Q6867
- Размер файла: 200 МБ
- ОС: Ubuntu 12.
 04/SteamOS
04/SteamOS
Скачать: | Через Steam |
|---|---|
Разработчик: | Образовательные игры |
Издатель: | Образовательные игры |
Категории: | Повседневный Инди |
| Сапер Дата выпуска : | 15 ноября 2017 |
Компьютер Sapper цена сегодня:
2,99 доллара США
Сапер дешево предлагает:
Трекер цен PCGB может попытаться предсказать следующую официальную скидку Steam The Sapper .

 04/SteamOS
04/SteamOS