Человека скорость бег: «Какова самая быстрая скорость бега человека?» – Яндекс.Кью
ЧЕЛОВЕК РОЖДЕН ДЛЯ БЕГА | Наука и жизнь
Ежегодный массовый марафон в Нью-Йорке. Как утверждает американский антрополог Д. Либерман, принимать участие в подобных мероприятиях людей заставляет эволюционное наследие.‹
›
Как утверждают американские антропологи Деннис Брамбл и Дэниел Либерман, еще два миллиона лет назад наши предки приобрели в эволюции необычайные способности к бегу на длинные дистанции.
Конечно, леопард обгонит человека в спринте, но на большой дистанции он да и почти все другие млекопитающие отстанут от двуногого бегуна. Человек даже обгонит малорослую лошадь — пони. Большинство млекопитающих не могут быстро бежать дольше 10-15 минут. Средняя скорость, которую спортсмен высокого класса способен поддерживать на протяжении двух часов, составляет 20,4 километра в час. Ни один из приматов этого не может.
Брамбл и Либерман перечисляют несколько особых приспособлений к длительному бегу, имеющихся у человека. Эти особенности строения тела не имеют отношения к прямохождению, а связаны именно с быстрым бегом.
Следы прикрепления мышц и связок на ископаемых костях ранних гоминид позволяют понять, когда появились эти приспособления к бегу. У австралопитека афарского (3-4 миллиона лет назад) таких особенностей еще нет, но у жившего 1,6-1,9 миллиона лет назад человека трудящегося (Homo ergaster) их признаки уже появляются.
Но зачем нашим предкам понадобилось научиться быстро бегать? На этот вопрос Либерман и Брамбл отвечают: чтобы обгонять гиен. Ранние представители нашего рода питались в саванне главным образом падалью, используя каменные орудия для того, чтобы отреза, ть от трупов животных куски мяса и разбивать трубчатые кости с вкусным костным мозгом. При этом надо было обогнать конкурентов.
При этом надо было обогнать конкурентов.
Необходимость в быстром беге утратила свою важность только после того, как человек изобрел «дальнобойное» охотничье оружие — дротики, копья, а затем и лук. Но еще до этого умение раньше всех добежать до богатого источника белков и жиров позволило развиться крупному мозгу, который и сделал эти и многие другие изобретения.
Как развить скорость реакции и движения, занимаясь функциональным тренингом
Достижение максимально возможной скорости реакции и движения – одна из основных целей занятий функциональным тренингом. Приступая к тренировкам, любой атлет мечтает о ловком теле, которое моментально реагирует на любой вызов. Предлагаем ряд доступных упражнений, которые позволят вам как можно быстрее добиться впечатляющих результатов.
- Бег из различных положений. Имеются в виду не только спортивные беговые стойки, но и необычные, порой неудобные для начала бега позы – упор лежа, сидя, лежа на животе или спине, в направлении, противоположном движению.
 Бегать можно поодиночке или в группе, но непременно на время. Рекомендуются короткие дистанции длиной 10-20 метров. Пробегайте их по 5-6 раз подряд, затем делайте 1-2-минутный перерыв и повторяйте серию забегов. В течение одной тренировки выполняйте 3-4 сета.
Бегать можно поодиночке или в группе, но непременно на время. Рекомендуются короткие дистанции длиной 10-20 метров. Пробегайте их по 5-6 раз подряд, затем делайте 1-2-минутный перерыв и повторяйте серию забегов. В течение одной тренировки выполняйте 3-4 сета. - Бег на дистанцию 30-60 метров с максимальным ускорением. Повторяйте по 3-4 забега в одной серии, по 3-4 серии забегов в течение одной тренировки. Делайте между сериями короткие перерывы для восстановления дыхания.
- Бег на 10-30 метров «без разбега». Стартуйте с места с максимальной скоростью. Делайте такое же количество повторов, как и в предыдущем упражнении.
- Быстрый бег в течение 20 секунд по холмистой местности или дороге, изобилующей перепадами высот. Бег перемежайте ходьбой в течение 1-2 минут, за тренировку выполняйте 3-4 сета.
- Примите боевую стойку, в течение нескольких минут делайте шаги вперед и назад, вправо и влево.
 Меняя стойки, проделайте несколько сетов по 1-2 минуты каждый.
Меняя стойки, проделайте несколько сетов по 1-2 минуты каждый. - Бег на четвереньках. Передвигайтесь так быстро, как можете, желательно в форме соревнования с напарником.
- Наносите одиночные удары по снаряду ногами и руками, стараясь делать это с максимальной частотой. При отсутствии боксерского мешка практикуйте удары по воздуху.
- Тренируйте серии ударов длительностью по 10 секунд каждая. В течение тренировки выполняйте 3-4 сета. Наносите удары ногами и руками, делая между ними перерывы по 2-3 минуты.
- Совершайте прыжки на месте, одновременно делая удары руками. Постарайтесь за один прыжок совершить как можно больше ударов. Делайте по 10-20 прыжков на каждую руку за одну сессию, всего 3-4 сессии за тренировку с перерывами на отдых.
- Бой из 3-4 раундов с воображаемым противником. Во время поединка с «тенью» наносите удары, проводите обманные маневры, уклоняйтесь от встречных ударов.
 Между раундами – отдых в течение 1-2 минут.
Между раундами – отдых в течение 1-2 минут. - Сложите вместе ладони рук и максимально быстро делайте ритмичные движения с большой амплитудой. Продолжительность упражнения – 5-10 секунд, выполните несколько серий в течение тренировки.
- Прыжки со скакалкой, чередование прыгания на скорость с прокручиванием снаряда два и более раз.
- Прыжки через скакалку, которую вращают два человека. Прыгать 5-6 минут постоянно ускоряясь.
- Упражнение выполняется с партнером. Ваша задача – уклоняться от мяча, который он в вас бросает. В процессе игры частота бросков увеличивается, либо дистанция между вами и бросающим сокращается. Продолжительность упражнения зависит от самочувствия.
- В упражнении задействованы два партнера. Один из них бросает мяч, другой защищает условные «ворота». Его задача – отбивать мяч, используя только руки либо только ноги. По мере выполнения упражнения условия игры можно делать более жесткими.

- «Кулачки» — традиционная игра для двоих, развивает быстроту и реакцию.
- Партнер наносит вам удары поочередно правой или левой рукой. Вы, находясь в защитной стойке, должны увернуться от них. В ходе выполнения упражнения можно менять руки, скорость ударов и другие правила.
- Бег вверх и вниз по лестнице с максимальной скоростью. Не перепрыгивая через ступеньки, делайте по 2-3 забега с минутными перерывами. В течение тренировки выполняйте 5-6 сессий.
- Бег на 100-метровую дистанцию с легкоатлетическими препятствиями. Делайте 6 забегов за тренировку.
- Запрыгивание на тумбу с моментальным соскоком. Высота тумбы должна повышаться с течением времени с 30 до 60 см. В течение тренировки выполняйте 3-4 подхода, по 10-20 прыжков в каждом.
- Броски правой и левой рукой теннисного мяча на дальность и в цель.
- Броски вверх баскетбольного и футбольного мяча.

- Компьютерные игры (Да-да!). Она развивают быстроту реакции, внимание, логику и память, но злоупотреблять ими не нужно.
Моделирование бега под дождем / Хабр
Вступление
Все началось с чрезвычайно провокационного, граничащего с дерзостью заявления, которое категорически не соответствует моим представлением об окружающем мире: «Можно меньше промокнуть, если бежать под дождем – это миф». Другими словами, из этого утверждения следует, что общеизвестным и общепринятым является тот факт, что бегущий под дождем человек промокнет сильнее, чем такой же человек прошедший пешком такое же расстояние, под тем же дождем. Но, какие-то, непроверенные не заслуживающие доверия источники утверждают обратное, что если вы побыстрее уберетесь из под дождя то промокнете меньше.
Это заявление прозвучало в телепрограмме Mythbusters (эпизод 001). Я несколько раз перепроверял — формулировка мифа именно такая: «A person will end up drier by running in the rain rather than walking».
Update: как подсказал rezdm есть видео с другой формулировкой «Is it worth running in the rain» вот и вот
Более того, результатом проверки оказалось разрушение этого мифа, то есть, ведущий, который бежал, промок сильнее ведущего, который шел!? То есть эти непроверенные и не заслуживающие доверия источники, со своими глупостями были поставлены на место. До того момента, в моем мире все было наоборот, и, чтобы меньше промокнуть, я старался бегом добраться до укрытия.
Далее, пару сезонов спустя, этот миф был перепроверен и опровергнут (эпизод 38). Но результаты и в первом и во втором случае оказались не очень показательными: разница собранной воды была небольшой, и вряд ли сильно отличалась от статистической погрешности, и от погрешности измерений на весах. В первом эксперименте дождь создавался путем подачи воды на разбрызгиватели, которые были подвешены под потолок высокого ангара. Во втором эксперименте работали с тем, что упадет с неба. После второго эксперимента ясности стало еще меньше.
Первый эксперимент мне понравился больше, так как там были контролируемые условия, причем эти условия можно было поддерживать необходимое время. В случае с обычным дождем условия постоянно меняются – дождь может прекратиться, измениться его интенсивность или подует ветер. На мой взгляд, нужно было продолжить первое исследование: можно было увеличить дистанцию, можно было поиграть с параметрами дождя чтобы сократить статистическую погрешность и сделать результаты более убедительными. Mythbusters — отличная телепрограмма, но в этом конкретном случае хотелось взять и все переделать. Особенно заинтересовала тема влияния характера дождя, на итоговое промокание, ведь обычно в таких экспериментах идет усредненный дождь, а ведь дождь бывает разный.
Как это обычно бывает, я мужественно преодолел это бессмысленное, навязанное желание переделать эксперимент и забыл о нем. Но лето в этом году в московском регионе как то слишком часто располагало к размышлениям на тему «так все-таки убегать ли мне от этого дождя, или идти спокойно». В результате решил написать небольшой проект и поисследовать, то, что было интересно, с помощью компьютерного моделирования. Как оказалось, в Московском регионе тема остается актуальной и сейчас в декабре.
В результате решил написать небольшой проект и поисследовать, то, что было интересно, с помощью компьютерного моделирования. Как оказалось, в Московском регионе тема остается актуальной и сейчас в декабре.
Со следующего раздела приводится описание того, что получилось, но здесь нужно сказать несколько слов, про историю вопроса. При подготовке статьи выяснилось, что вопрос «идти или бежать под дождем» не дает покоя множеству гиков по всему свету уже довольно давно. Видимо, первым поднял волну, известный популяризатор науки Яков Исидович Перельман, в его книге «Занимательная механика» (видел только 4е издание 1937г., но возможна задача была и в более ранних начиная с 1930 г.) В девятой главе «Треняе и сопротивление среды» (да тренЯе, начало двадцатого век все — таки) последний раздел называется «Когда дождь промочит сильнее?», но фактически задача звучит так «В каком случае вы больше промочите свою шляпу?». Тут есть разница — в книге речь идет только о той составляющей дождя, которую шляпа воспринимает сверху, о столкновении с дождем в вертикальной плоскости речи не идет. К тому же в задаче эксперимент проводится при одинаковом времени, пребывания под дождем, в то время как нас интересует одинаковое расстояние. Нет никаких сомнений в справедливости, приведенного в книге решения, но само название раздела, и самостоятельные выводы читателей могли привести к неправильным выводам и появлению стереотипа.
К тому же в задаче эксперимент проводится при одинаковом времени, пребывания под дождем, в то время как нас интересует одинаковое расстояние. Нет никаких сомнений в справедливости, приведенного в книге решения, но само название раздела, и самостоятельные выводы читателей могли привести к неправильным выводам и появлению стереотипа.
После Перельмана были статьи в научно-популярных журналах древних и не очень, потом видосы вот, и вот перевод даже есть на хабре вот здесь. Еще одна статья, мимо которой трудно пройти – это статья 2012 года итальянского физика Франко Боччи в European Journal of Physics, саму статью, вряд ли читало большое количество людей, но про нее очень много писали в СМИ, например вот интересно написано, на мой взгляд. Есть и другие исследования разной степени серьезности. Оказалось, что история этой проблемы, возможно не менее интересна, чем сама проблема, и, возможно может быть предметом отдельной статьи.
Моделирование
Ограничения и допущения
Суть моделирования – это целенаправленное упрощение и абстрагирование восприятия реальности. Представленная в статье модель — не исключение. Далее в тексте могут быть указания, на то, что та или иная особенность, обусловленная спецификой задачи, физическими, когнитивными ограничениями, а также ограничениями связанные религиозными, расовыми, политическими, сексуальными и прочими предпочтениями автора, является допущением или ограничением (другими словами те вещи, которые было не только лень делать, но еще и лень объяснять, почему я их не сделал).
Представленная в статье модель — не исключение. Далее в тексте могут быть указания, на то, что та или иная особенность, обусловленная спецификой задачи, физическими, когнитивными ограничениями, а также ограничениями связанные религиозными, расовыми, политическими, сексуальными и прочими предпочтениями автора, является допущением или ограничением (другими словами те вещи, которые было не только лень делать, но еще и лень объяснять, почему я их не сделал).
Примеры ограничений и допущений: Количество капель в ячейке одна (ограничение на максимальную интенсивность), все капли имеют одинаковый размер, предполагается что человек во время ходьбы и бега не машет руками и ногами (площадь фронтальной и горизонтальной проекции всегда одинакова), вода поднятая с ботинок на спину не учитывается, ветра в эксперименте нет и пр.
Пространство и человек
Пространство
Модель представлена двумя объектами пространство и человек.
Пространство – это прямоугольный параллелепипед, разбитый на кубики размером 1х1х1 см.
Ширина пространства равна ширине человека: в проведенном эксперименте не рассматриваются случаи с ветром, и с боковым ветром, поэтому обсчитывать пространство за пределами ширины человека нет никакого смысла.
Высота пространства больше высоты человека на один горизонтальный слой кубиков – то есть на один сантиметр, в этом слое начинают регистрироваться капли, которые в следующий момент времени упадут на человека, или дальше в пространство не занятое человеком.
Длина (протяженность) пространства – должна быть равна длине дистанции, но это очень неэкономично, так как для эксперимента нужно знать только о состоянии пространства над человеком, и о нескольких слоях перед ним. Поэтому в проекте пространство используется циклично, а его длина выбирается такой, чтобы к моменту, когда человек полностью его пройдет в первом вертикальном слое обновились все ячейки. Другими словами капля, которая появилась в слое, находящимся сразу за спиной человека должна иметь достаточно времени, чтобы упасть на землю, к тому моменту, когда человек вновь приблизится к этому слою лицом. Таким образом, при правильном подборе длины пространства на человека всегда будут капать свежие капли.
Таким образом, при правильном подборе длины пространства на человека всегда будут капать свежие капли.
Нужно отметить, что при проведении эксперимента длина пространства устанавливается единожды, и далее не меняется, поэтому для начальной установки значения длинны, выбиралось такое соотношение параметров, чтобы во всех случаях длина была достаточная (максимальная скорость человека и минимальная скорость падения капель).
Пространство для эксперимента можно вообразить по разному, например как замкнутый коридор, но мне больше нравится представлять его прямоугольным пятном света, от фонаря, который светит с боку на человека, и которое движется вместе с человеком. Каждая капля, которая попадает в свет внутри пятна, регистрируется. Такой подход позволяет отделить понятие физического, бесконечного пространства, в котором под дождем бегает человек, от пространства эксперимента — воображаемой трехмерной сетки, состояние каждой ячейки которой проверяется в каждый момент времени эксперимента. В статье слово «пространство» используется во втором значении.
В статье слово «пространство» используется во втором значении.
В программе пространство представлено трехмерным байтовым массивом. Индексы элемента в массиве соответствуют координатам ячейки в пространстве (протяженность, высота, ширина), сам элемент описывает состояние. Состояния может быть только два – в ячейке есть капля дождя или ячейка пустая.
Пространство также можно представить как набор горизонтальных слоев, сквозь которые падает дождь, и как набор вертикальных слоев с которыми, двигаясь, сталкивается человек. В программе, есть классы – обертки, отвечающие за эти представления.
Человек
Человек в проекте – это просто прямоугольный параллелепипед. Для эксперимента в первую очередь нам интересны его проекция на горизонтальную плоскость для подсчета капель, падающих сверху, и проекция на вертикальную плоскость, перпендикулярную направлению движения, для подсчета капель с которыми человек сталкивается, двигаясь вперед. Также используется координата, отвечающая за его положение в пространстве, и счетчики собранной воды спереди и сверху.
Для того, чтобы оценить площадь горизонтальной проекции погуглил, одна из первых ссылок была на какой-то нормативный акт, который использует МЧС. Там горизонтальная проекция человека представлена эллипсом с размерами осей 0,5 м (ширина человека в плечах) и 0,25 м (толщина человека). Похоже на правду, поэтому взял прямоугольник почти такой же площади (S эллипса=pi*a*b S = 3.14*(50/2)*(25/2) ~ 982 кв. см, прямоугольник 48 на 20 = 960 кв. см). Как было показано выше, эти данные используются, в том числе для определения ширины и протяженности пространства. Определения вертикальной проекции человека не нашел, поэтому для роста взял величину чуть меньше среднего — 160 см. Размерность человека легко меняется в проекте, но эксперимент проводился только на одном наборе параметров. Так как, этот вопрос показался мне не очень интересным – во первых во время дождя вряд ли на эти параметры можно как-то повлиять, а во вторых выяснение того, какое телосложение оптимально для промокания под дождем может показаться кому-то обидным. Отношу это к ограничениям и допущениям.
Отношу это к ограничениям и допущениям.
Скорость человека: за нижний предел взята скорость 2,196 км/ч взята вот отсюда видимо эти данные используются для целей протезирования, верхний предел — 43.9 км/ч — самая быстрая на данный момент зафиксированная скорость бега.
Про дождь
Дождь в проекте это процесс, который происходит в пространстве, и который имеет свои характеристики: размер капли, скорость падения, интенсивность.
По данным Википедии диаметр дождевой капли не может быть меньше 0.5 мм, так как это будет уже не дождь, а морось, и не больше 6-7 мм, при таких условиях капли распадаются на более мелкие.
В соответствии с той же статьей скорость падения капель варьируется от 2 до 6 м/с для мелких капель и от 9 до 30 м/с для капель с диаметром 5 мм. При размере от 5мм до 7мм скорость падения снижается из-за того, что такие крупные капли приобретают форму парашюта, и сопротивление воздуха растет. Скорость падения капель зависит не только от размера самой капли, но и от условий в которых она падает – предполагаю, что от плотности воздуха, наличия восходящих или нисходящих потоков, и пр.
В проекте установлена линейная зависимость скорости падения от длины диаметра: в диапазоне диаметров от 0.5 до 5 мм скорость линейно возрастает от 2м/с до 30 м/с (DropSize*6.22 – 1.11), в диапазоне от 5 мм до 7 мм скорость снижается с той же интенсивностью ((10 — DropSize)*6.22 – 1.11), за пределами диапазона 0.5 – 7 мм эксперимент не проводится.
Линейная зависимость, используемая в эксперименте, не противоречит существующей картине мира, но она ограничена, и поэтому является допущением. К примеру, размеру капли 5мм в проекте соответствует скорость 30 м/с – в реальном мире такое вполне может быть (если верить Википедии), но в реальном мире также возможно, что капля диаметром 5мм будет падать гораздо медленнее — со скоростью 9 м/с. Если кто-то заинтересуется и решит сам поэкспериментировать, то можно изменить зависимость на любую другую, или даже поэкспериментировать с несколькими. В данном проекте эта фича будет использована в очень ограниченном объеме (из – за нехватки времени).
Интенсивность – еще одна интересная, и важная характеристика дождя. Интенсивность обычно указывается в миллиметрах в час. Один миллиметр в час означает, что за один час на горизонтальную поверхность площадью один квадратный метр выпадет слой воды толщиной один миллиметр. Не трудно посчитать, что объем этого слоя воды – один литр. То есть один мм/ч это то же самое что один литр на один квадратный метр за один час. Иногда в прогнозах погоды, когда хотят описать масштаб бедствия, указывают просто миллиметры — это уже посчитанная высота слоя воды, выпавшей за всю продолжительность дождя. В проекте, и далее в статье будет использоваться единица измерения — миллиметры в час.
В соответствии с Википедией интенсивность дождя обычно составляет от 0,25 мм/ч (моросящий дождь) до 100 мм/ч (ливень) – эксперимент проводился в границах этих значений.
Про распределение капель в пространстве:
Есть один интересный момент, на котором хотелось бы ненадолго остановиться. На стадии проектирования планировалось, что верхний горизонтальный слой, будет заполняться каплями следующим образом: один раз вычисляется вероятность появления капли в ячейке, а затем, перебирая все ячейки слоя, рандомайзер, исходя из этой вероятности, будет помещать в ячейку каплю, или не помещать. Вероятность вычислялась как отношение необходимого количества капель в слое к общему количеству ячеек в слое. С учетом того, что пространство и так сокращенно до минимума такой подход представлялся вполне разумным. Однако перед началом эксперимента решил оценить количество капель на единицу пространства (ту самую веросятность появления) и вот что получилось: Ниже представлены графики количества капель в слое площадью один квадратный метр и толщиной один сантиметр, в зависимости от размера капли, каждый график соответствует своей интенсивности:
На стадии проектирования планировалось, что верхний горизонтальный слой, будет заполняться каплями следующим образом: один раз вычисляется вероятность появления капли в ячейке, а затем, перебирая все ячейки слоя, рандомайзер, исходя из этой вероятности, будет помещать в ячейку каплю, или не помещать. Вероятность вычислялась как отношение необходимого количества капель в слое к общему количеству ячеек в слое. С учетом того, что пространство и так сокращенно до минимума такой подход представлялся вполне разумным. Однако перед началом эксперимента решил оценить количество капель на единицу пространства (ту самую веросятность появления) и вот что получилось: Ниже представлены графики количества капель в слое площадью один квадратный метр и толщиной один сантиметр, в зависимости от размера капли, каждый график соответствует своей интенсивности:
По горизонтальной оси – размер капли, по вертикальной оси – количество капель. Вертикальная ось – логарифмическая, так как разброс количества капель очень большой. Такой большой разброс объясняется тем, что объем капли пропорционален третьей степени от ее линейных размеров (диаметра), плюс с увеличением размера капли увеличивается скорость ее падения. Соответственно при небольшом изменении диаметра капли количество капель в объеме меняется очень сильно (например, для интенсивности дождя 80 мм/ч, при диаметре капли 0.8 мм требуется около 215 капель на слой, а при увеличении диаметра капли в два раза – до 1.6 мм, всего 12 капель на слой).
Такой большой разброс объясняется тем, что объем капли пропорционален третьей степени от ее линейных размеров (диаметра), плюс с увеличением размера капли увеличивается скорость ее падения. Соответственно при небольшом изменении диаметра капли количество капель в объеме меняется очень сильно (например, для интенсивности дождя 80 мм/ч, при диаметре капли 0.8 мм требуется около 215 капель на слой, а при увеличении диаметра капли в два раза – до 1.6 мм, всего 12 капель на слой).
Теперь, что касается оптимизации: как видно из графиков даже при минимальном объеме капли и максимальной интенсивности количество капель на 10 тысяч ячеек – не превышает 2 х тысяч, в большинстве случаев количество капель менее 100, а при размере диаметра капли более 3мм количество капель на слой меньше одной. Соответственно перебирать каждую ячейку слоя, чтобы в конечном итоге в нем оказалась только одна капля не экономично. Более экономичный вариант – вычислить количество капель в слое, а затем случайным образом разбросать их по слою. Единственное усложнение — это случай, когда выбранная ячейка оказывается уже заполненной (в этой ситуации красиво смотрится рекурсия). Если к этому всему добавить запоминание заполненных ячеек, для последующей очистки слоев, то можно получить значительную экономию по CPU, при незначительном увеличении использования RAM.
Единственное усложнение — это случай, когда выбранная ячейка оказывается уже заполненной (в этой ситуации красиво смотрится рекурсия). Если к этому всему добавить запоминание заполненных ячеек, для последующей очистки слоев, то можно получить значительную экономию по CPU, при незначительном увеличении использования RAM.
Процесс эмулирования дождя
Процесс моделирование происходит в одном главном цикле. Каждая итерация этого цикла соответствует минимальному интервалу времени (тик). Каждый тик состояние системы обновляется и фиксируется. Продолжительность тика соответствует продолжительности пролета капли дождя через один слой пространства (в нашем случае 1см), поэтому один тик в программе может соответствовать различным интервалам времени в реальной жизни, в зависимости от входных параметров (а точнее от скорости падения капель). Ниже описаны действия, происходящие внутри каждой итерации:
Процесс дождя в проекте выглядит следующим образом: сначала верхний слой случайным образом заполняется каплями (см. раздел выше), пусть это будет слой номер n. В следующей итерации капли из n-го слоя проваливаются в ячейки слоя, расположенного прямо под ними — в слой номер n-1, верхний слой снова заполняется. Далее все происходит аналогично: в слой номер n-2 проваливаются капли слоя n-1, в слой n-1 капли n-ного, а n-ный снова заполняется случайным образом, и так далее. Когда капли, достигнут самого нижнего слоя, они никуда не проваливаются, а просто исчезают (скажем, падают на землю, и впитываются), и далее, после очистки, этот слой поднимается наверх и переиспользуется.
раздел выше), пусть это будет слой номер n. В следующей итерации капли из n-го слоя проваливаются в ячейки слоя, расположенного прямо под ними — в слой номер n-1, верхний слой снова заполняется. Далее все происходит аналогично: в слой номер n-2 проваливаются капли слоя n-1, в слой n-1 капли n-ного, а n-ный снова заполняется случайным образом, и так далее. Когда капли, достигнут самого нижнего слоя, они никуда не проваливаются, а просто исчезают (скажем, падают на землю, и впитываются), и далее, после очистки, этот слой поднимается наверх и переиспользуется.
Перебор каждой ячейки пространства для того чтобы скопировать (опустить ниже) все капли, выполняющийся в каждой итерации довольно затратная операция. Для того чтобы оптимизировать этот процесс, в классе пространства есть указатель, этот указатель циклически перемещается по номерам горизонтальных слоев (каждую итерацию он инкрементируется на единицу). Номер слоя соответствующий указателю на данной итерации считается верхним. Технически изменяется указатель, но, как известно, движение относительно, и если привязать систему отсчета к указателю, то данный процесс можно представить себе как движение (вертикальное падение) стопки горизонтальных слоев мимо неподвижного указателя, на котором отражается номер того слоя, который в данный момент пролетает мимо него.
Технически изменяется указатель, но, как известно, движение относительно, и если привязать систему отсчета к указателю, то данный процесс можно представить себе как движение (вертикальное падение) стопки горизонтальных слоев мимо неподвижного указателя, на котором отражается номер того слоя, который в данный момент пролетает мимо него.
Процесс эмулирования движения человека
В классе человека есть указатель, который циклически перемещается по вертикальным слоям, перпендикулярным направлению движения (фронтальные слои), этот указатель указывает на слой, расположенный перед самым его носом, и используется для определения пятна на верхнем слое, капли из которого падают на человека сверху.
В программе также есть переменная (число с плавающей точкой), которая отражает точное текущее положение человека (пройденное расстояние). Зная скорость падения капель, можно вычислить время соответствующее одному тику. Умножив продолжительность тика на скорость человека, получаем расстояние, проходимое человеком за один тик. Каждую итерацию пройденное расстояние инкрементируется на расстояние, проходимое за один тик. Если человек остается в том же слое — указатель на вертикальный слой не инкрементируется, счетчик воды собранной спереди никак не изменяется. Если человек переходит в следующий слой, указатель на вертикальный слой инкрементируется на единицу, а счетчик воды собранной спереди увеличивается на количество капель, находящихся в данный момент в вертикальном слое, на который указывает указатель. Если человек за один тик проходит несколько слоев, то счетчик увеличивается на количество капель находящихся во всех пройденных слоях, а указатель инкрементируется на число пройденных слоев.
Каждую итерацию пройденное расстояние инкрементируется на расстояние, проходимое за один тик. Если человек остается в том же слое — указатель на вертикальный слой не инкрементируется, счетчик воды собранной спереди никак не изменяется. Если человек переходит в следующий слой, указатель на вертикальный слой инкрементируется на единицу, а счетчик воды собранной спереди увеличивается на количество капель, находящихся в данный момент в вертикальном слое, на который указывает указатель. Если человек за один тик проходит несколько слоев, то счетчик увеличивается на количество капель находящихся во всех пройденных слоях, а указатель инкрементируется на число пройденных слоев.
Счетчик капель, упавших сверху обновляется каждый тик, без исключения. Как было указанно выше, расположение пятна, из которого капли попадут на человека, определяется указателем на фронтальный слой.
Собственно про модель, и про то, как она работает все сказано, далее предлагаю перейти к экспериментам.
Эксперименты и выводы
Цели и задачи
Перед экспериментом предлагаю определить и формализовать вопросы, ради которых все затевалось.
Первый, и самый главный вопрос – «Правда ли, что можно меньше промокнуть под дождем, если идти, а не бежать до укрытия?» Более формально – «Как влияет скорость человека на итоговый объем собранной воды при прочих равных условиях?»
Второй. Если на первый вопрос будет дан ответ «нет», но мы то знаем, что разрушителям легенд удалось воспроизвести ситуацию, когда бегущий человек промок сильнее пешехода, то возникает вопрос: Возможна ли ситуация, когда бегущий человек промокнет сильнее идущего и при каких условиях это возможно?
Третий. «Как влияет размер капель на итоговый объем собранной воды при прочих равных условиях?»
Четвертый. «С какой стороны человек соберет больше воды – сверху, или спереди? От чего зависит это соотношение?»
Определение понятий
Для удобства описания необходимо определить несколько понятий, иначе будет легко запутаться. Итак: далее человека буду называть Катя, это немного сократит объем текста, и добавит в рассказ еще больше веселья, угара и легкомыслия. В эксперименте Кате нужно будет проходить или пробегать расстояние в 1 километр, одно прохождение дистанции от начала до конца будет называться забег.
В эксперименте Кате нужно будет проходить или пробегать расстояние в 1 километр, одно прохождение дистанции от начала до конца будет называться забег.
Далее, для того, чтобы оценить влияние скорости на объем собранной воды Кате нужно при одних и тех же условиях сделать несколько забегов с разными скоростями. В нашем случае это будут скорость медленного прогулочного шага 2,2 км/ч, скорость быстрого бега 23,04 км/ч, и скорость самого быстрого бега, которую только способен развить человек 43,88 км/ч. Все три забега вместе буду называть
Далее, так как нас интересует влияние характера дождя, нужно попросить Катю пробежать несколько сетов при разных условиях. Модель предоставляет возможность влиять на две характеристики дождя – размер капли и интенсивность, для удобства их можно организовать иерархически, например, размер капли будет более низким звеном по отношению к интенсивности. Тогда Кате нужно будет пробежать несколько сетов с разным размером капель, но постоянной интенсивностью. Так как сет сетов не самое благозвучное название буду называть его суперсетом, хотя тоже не огонь. Ну и на самом верхнем уровне иерархии у нас будет интенсивность, которая включает несколько мегасетов при разной интенсивностью, этот сет суперсетов буду называть
Тогда Кате нужно будет пробежать несколько сетов с разным размером капель, но постоянной интенсивностью. Так как сет сетов не самое благозвучное название буду называть его суперсетом, хотя тоже не огонь. Ну и на самом верхнем уровне иерархии у нас будет интенсивность, которая включает несколько мегасетов при разной интенсивностью, этот сет суперсетов буду называть

Во время проведения эксперимента будут сниматься следующие показатели:
для каждого забега:
— объем полученной воды;
— количество капель всего;
— количество (объем) капель сверху;
— количество (объем) капель спереди;
— средний прирост за один тик;
— средний прирост сверху за один тик;
— средний прирост за одно горизонтальное смещение (всего / только горизонтальные/ только фронтальные)
для каждого сета
— разница полученного объема на разных скоростях.
— другие показатели, которые придут в голову.
Результаты и выводы
Итак, первый эксперимент прошел. Он состоял из одной серии, трех суперсетов, 12 сетов, и 36 забегов на дистанцию 1 км. Всего в базу было сделано 32 529 927 записей, время выполнения на моей чахлой машине чуть больше 2 часов. Ниже сводная таблица, уже после обработки результатов, в которой приведен общий объем полученной воды в каждом забеге, и параметры забегов.
В последнем столбце приведена разница собранной воды от забега к забегу в каждом сете. Напомню, что в одном сете забеги отличаются только скоростью прохождения дистанции. Как видно в последнем столбце нет ни одного отрицательного числа, соответственно ответ на первый вопрос: «Как влияет скорость человека на итоговый объем собранной воды при прочих равных условиях?» Ответ: Итоговый объем собранной воды всегда меньше при большей скорости движения человека. Проведенный эксперимент наглядно это демонстрирует.
Тут, казалось бы, должен быть очевидный ответ на второй вопрос «Возможна ли ситуация, когда бегущий человек промокнет сильнее идущего и при каких условиях это возможно?» — нет, не возможно, и разрушители что-то накосячили. Но давайте посмотрим на третий сет:
Разница собранной воды при быстром беге и очень быстром беге (отличие 20 км/ч) на дистанции 1 километр, дало очень небольшое преимущество 3.2 мл в абсолютном выражении и ~ 26% в относительном. Для справки, распределение капель в пространстве при такой интенсивности и при таком диаметре очень небольшая: вероятность появления капли в слое равна 0,0005841873 или 1 капля на 1712 слоев, или 1 капля на 7,06 кубических метров. Так как появление капли в том или ином месте – это случайный процесс, и если сократить разницу в скоростях, и дистанцию, то результаты станут более случайными, в этом случае возможно всякое, в том числе более сильное промокание на более низкой скорости см. таблицу ниже.
Для справки, распределение капель в пространстве при такой интенсивности и при таком диаметре очень небольшая: вероятность появления капли в слое равна 0,0005841873 или 1 капля на 1712 слоев, или 1 капля на 7,06 кубических метров. Так как появление капли в том или ином месте – это случайный процесс, и если сократить разницу в скоростях, и дистанцию, то результаты станут более случайными, в этом случае возможно всякое, в том числе более сильное промокание на более низкой скорости см. таблицу ниже.
Эта таблица отражает результат дополнительных 20 забегов на короткую дистанцию 100 м, с небольшой интенсивностью и крупными каплями дождя. Как видно диапазон значений собранной воды на скорости 23 км/ч частично пересекается с диапазоном значений собранной воды на скорости 43 км/ч. Это означает, что ответ на вопрос о том, можно ли собрать больше воды на большей скорости будет звучать так «Да возможно, при небольшой разнице скоростей и маленькой выборке». Если перефразировать на нормальный язык: если идет несильный дождь с крупными и редкими каплями, и идти до укрытия не очень далеко, то итоговое промокание скорее будет зависеть от вашей удачи, нежели от вашей скорости.
Третий вопрос, «Как влияет размер капель на итоговый объем собранной воды при прочих равных условиях?».
Давайте перегруппируем таблицу, чтобы в третьем столбе были размеры капель, а во втором Катина скорость:
Как видно в диапазоне от 0.6 до 5 мм чем меньше объем капли, тем больше общий полученный объем воды, но в диапазоне 5 – 7 мм наоборот (с каплей размером 7 мм воды собирается больше, чем с каплей 5мм). Для поиска зависимостей в таблицу ниже добавлены столбцы с количеством капель в слое, скоростью падения капель, и количеством собранных капель всего за забег.
Как видно, объем собранной воды напрямую коррелирует только со скоростью падения капель – чем меньше скорость, тем больше объем собранной воды. Поскольку скорость является производной величиной, зависящей только от размера капли (в нашей модели), то ответ на третий вопрос может звучать так: При размере капель соответствующих минимальной скорости падения объем собранной воды будет максимальным, и наоборот, при размере капель соответствующих максимальной скорости общий собранный объем будет минимальным.
Однако здесь требуется уточнение – что будет, если одной и той же скорости соответствует несколько размеров капель.
Чтобы это проверить, пришлось провести дополнительную серию экспериментов на интенсивности 50мм/ч с изменением зависимости скорости от размера капли (а точнее трижды прибить гвоздями скорость падения). Вот, что получилось:
Как видно из таблицы, при прочих равных условиях, итоговый объем воды, собранной человеком зависит только от соотношения скорости человека и скорости падения капель, и не зависит от размера капли.
Выводы из этого наблюдения вряд ли имеют какую-либо практическую ценность, потому что здесь результаты сравниваются для строго определенных интенсивностей. В реальном мире, обычно увеличение размера капель и скорости их падения говорит об увеличении интенсивности. Другими словами, несмотря на эту красивую таблицу, если вас во время прогулки застанет ливень с крупными и быстрыми каплями, очень вероятно, что он промочит вас гораздо сильнее, чем обычный затяжной дождь с мелкими и медленными каплями потому, что интенсивность ливня будет гораздо сильнее.
Четвертый вопрос: «С какой стороны человек соберет больше воды – сверху, или спереди? От чего зависит это соотношение?».
В таблице ниже приведена наша изначальная группировка, опущен общий объем, но добавлены количества капель сверху, спереди, их соотношение и их общее количество.
При анализе таблицы можно сделать несколько выводов, начну с наиболее очевидных:
1) Соотношение сильно зависит от скорости человека – чем медленнее движется человек, тем больше капель падает сверху (в каждом сете чем выше скорость тем меньше капель собранных сверху).
2) Если идти очень медленно, то независимо от того, какой идет дождь больше половины капель будет собранно сверху (абсолютно во всех сетах при скорости 2 км/ч количество капель полученных сверху больше 50 %).
3) Соотношение практически не зависит от интенсивности дождя, если сравнить соответствующие соотношения в суперсетах, то видно, что они отличаются совсем незначительно, или не отличаются вообще (таблица ниже).
4) Соотношение сильно зависит не только от скорости Кати, но и от скорости падения капель. Если посмотреть на дельты значений соотношений с максимальной и минимальной скоростью Кати, то получится что максимальный разброс соответствует размеру капли с максимальной скоростью падения (таблица ниже):
Это означает, что чем больше скорость падения капель, тем сильнее Катя может повлиять на итоговый объем собранной воды. Другими словами если вас застал ливень, который хлещет крупными каплями, то чем быстрее вы добежите до укрытия, тем меньше промокнете. И наоборот, если на улице морось, множество мелких, висящих в воздухе капель, то бежать особого смысла нет, это не сильно повлияет на итоговый результат.
Таким образом, ответ на четвертый вопрос «С какой стороны человек соберет больше воды – сверху, или спереди? От чего зависит это соотношение?» звучит так: Человек, идя под дождем, может собрать больше воды как сверху, так и спереди, это соотношение, прежде всего, зависит от его скорости, но также большое влияние имеет скорость падения капель. Чем больше скорость человека, тем меньше капель упадет на него сверху.
Чем больше скорость человека, тем меньше капель упадет на него сверху.
На этом пожалуй, все. Как говорит доктор Скотт, палеонтолог, изучайте природу и делайте собственные открытия, ребята. 🙂
P.S. В тексте, в модели, в результатах, в поставленных вопросах и ответах на них, и в любых других местах могут быть ошибки, поэтому выкладываю проект в открытый доступ, если кто-то захочет проверить, перепроверить, повторить, дополнить, опровергнуть, ткнуть носом, и пр. – милости прошу github.com/sv-kopylov/raindrops-pub.git.
P.P.S Эта статья, является продолжением, теперь уже цикла статей про занимательное компьютерное моделирование, первая статья вот.
С какой скоростью бегают домашние кошки различных пород?
Первым надо поддерживать хорошую спортивную форму, чтобы ловить мышей и птиц, а также спасаться от извечных врагов – собак. Для них умение быстро бегать необходимо для выживания.
Вторым охотиться нужно только на бантик на веревочке или на полную миску, а спасаться – если только от хозяйского тапка. Выживать им не надо – хозяева обо всем позаботятся.
Выживать им не надо – хозяева обо всем позаботятся.
Молодое и активное животное может просто бешено носиться и играть. Умудренный жизнью кошачий ветеран сбережет все силы для молниеносного спринтерского броска.
В целом считается, что максимальная скорость, которую могут развивать эти животные, достигает почти 50 километров в час.
Самой быстрой кошкой называют представителей породы египетский мау. У этих животных особое строение задних конечностей. В основании лапы у них есть дополнительные кожистые складки. Во время бега они помогают увеличить запас шага и амплитуду движений, что добавляет скорости.
Среднюю скорость кошачьего бега фелинологи определяют цифрой в 13,5- 13,8 километров в час.
А скорость трусящей неторопливой рысцой кошки немногим больше скорости спокойно шагающего человека – около 8 километров в час.
Техника кошачьего бега
Кошка ухитряется мчаться прыжками, каждый из которых превышает длину ее тела в шесть раз! Помогают ей в этом попарно работающие передние и задние конечности. Толчок задними ногами – затяжной прыжок – приземление на передние, затем на задние лапы – снова толчок и прыжок.
Толчок задними ногами – затяжной прыжок – приземление на передние, затем на задние лапы – снова толчок и прыжок.
Когда животное просто прогуливается, когти втянуты, и оно наступает на подушечки лап. Нужно торопиться – и выпущенные когти способствуют лучшему сцеплению с поверхностью, помогая надежно оттолкнуться для прыжка.
Хвост выступает в роли балансира и регулятора направления движения. Правда, бобтейлы и иные бесхвостые породы прекрасно приспособлены обходиться и без этого кошачьего украшения. Прыгают они ничуть не хуже, бегают ничуть не медленнее хвостатых собратьев. Однако, если животное осталось без хвоста в результате несчастного случая или какого-то заболевания, приспосабливаться к полноценной жизни и активности оно будет долго.
Кошки – не марафонцы, а спринтеры
Но природа, наградив кошачьих быстротой и ловкостью, обделила их выносливостью. Как и большие собратья-гепарды, обычные кошки не могут бежать долго с большой скоростью. Разница в том, что дикие старшие братья рискуют лишь не наполнить желудок, а для младших домашних не успеть убежать – смерти подобно.
Разница в том, что дикие старшие братья рискуют лишь не наполнить желудок, а для младших домашних не успеть убежать – смерти подобно.
Сердце кошки не приспособлено к длительной работе в условиях экстремальных нагрузок. Начальная скорость высока и позволяет спастись. Но если кота гонят собаки и по пути не найдется подходящего дерева или надежного укрытия, то животное начнет задыхаться и погибнет (не от собачьих зубов, так от безумного перегруза и стресса).
Почему даже самый быстрый человек не может обогнать вашего домашнего кота
В эти выходные самые быстрые спринтеры планеты собрались на Олимпийских играх в Токио, чтобы побороться за золото в беге на 100 метров. Ламонт Марселл Якобс пересек финишную черту за 9,80 секунды, что принесло Италии первое золото в гонке. В женской гонке Ямайка выиграла золото, серебро и бронзу — чистый результат во главе с Элейн Томпсон-Хера, которая побила 33-летний олимпийский рекорд среди женщин со временем 10,61 секунды.
Но ни один из них не смог прикоснуться к наследию восьмикратного олимпийского призера Ямайки Усейна Болта, который ушел в отставку в 2017 году, но все еще может похвастаться титулом самого быстрого из ныне живущих людей. Болт пробежал 100 метров за 9,58 секунды. Максимальная скорость составляет около 27 миль в час, что чуть ниже максимальной скорости домашней кошки. (Да, домашний кот.) В гонке с гепардами и вилорогами, самыми быстрыми животными в мире, у Болта не будет ни единого шанса.
Вы можете подумать, насколько быстро животное может двигаться, зависит от размера его мускулов: больше силы, больше скорости.Хотя до некоторой степени это верно, слон никогда не убегает от газели. Так что же на самом деле определяет максимальную скорость?
Недавно группа ученых во главе с биомехаником Майклом Гюнтером, работавшая тогда в Штутгартском университете, задумала определить законы природы, которые определяют максимальную скорость бега в животном мире. В новом исследовании, опубликованном на прошлой неделе в журнале Journal of Theoretical Biology , они представляют сложную модель, учитывающую размер, длину ног, плотность мышц и многое другое, чтобы выяснить, какие элементы дизайна тела являются наиболее важными для оптимизации скорости.
Это исследование дает представление о биологической эволюции ножных животных и их соответствующих походок, и оно может быть использовано экологами для понимания того, как ограничения скорости передвижения животных влияют на популяцию, выбор среды обитания и динамику сообществ у различных видов. Для робототехников и биомедицинских инженеров изучение оптимальных для скорости структур тела в природе могло бы еще больше улучшить конструкцию двуногих ходильных машин и протезов.
«Речь идет о понимании причин эволюции, а также о том, почему и как она формирует тело», — говорит Гюнтер о цели проекта.«Если вы зададите этот вопрос механически, вы действительно сможете расширить понимание того, как дизайн тела формируется эволюционными требованиями — например, быстрота».
Предыдущая работа в этой области, проведенная под руководством Мириам Хирт из Немецкого центра интегративных исследований биоразнообразия, показала, что ключ к скорости связан с метаболизмом животных, процессом, с помощью которого организм превращает питательные вещества в топливо, конечное количество который накапливается в мышечных волокнах для использования во время спринта. Команда Хирта обнаружила, что у более крупных животных это топливо заканчивается быстрее, чем у более мелких, потому что им требуется больше времени, чтобы разогнать более тяжелые тела.Это называется мышечной усталостью. Это объясняет, почему теоретически человек мог обогнать тираннозавра.
Команда Хирта обнаружила, что у более крупных животных это топливо заканчивается быстрее, чем у более мелких, потому что им требуется больше времени, чтобы разогнать более тяжелые тела.Это называется мышечной усталостью. Это объясняет, почему теоретически человек мог обогнать тираннозавра.
Но Гюнтер и его коллеги были настроены скептически. «Я подумал, что мы могли бы дать другое объяснение, — говорит он, — которое использовало только принципы классической физики для объяснения ограничений скорости. Таким образом, они построили биомеханическую модель, состоящую из более чем 40 различных параметров, касающихся конструкции тела, геометрии бега и баланса конкурирующих сил, действующих на тело.
Человеческой скорости нет предела
Усэйн Болт, кажется, бежит невероятно быстро: его рекордное время в 9,58 секунды в 100-метровом спринте кажется непревзойденным, но именно это и раньше говорили о многих рекордсменах.
Но ведь должен быть жесткий предел человеческой скорости, после которого рекорды больше не будут бить? В конце концов, люди не могут бегать бесконечно быстро.
Питер Вейанд, физиолог, изучавший биомеханику бега на протяжении двух десятилетий, говорит, что нет.
«Вы всегда можете быть уверены, что независимо от того, как быстро кто-то бежит, можно двигаться быстрее», — говорит он Inverse . «У вас никогда не будет абсолютно идеальных условий, чтобы абсолютно идеальный человек и абсолютно идеальная гонка объединились одновременно».
Вот интересный факт: если вы можете спринт, , вы можете быть такими же быстрыми, как Усэйн Болт. Еще в конце 1990-х Вейанд и группа исследователей измерили множество разных людей, бегающих с максимальной скоростью, и у них было нечто общее: с очень небольшим отрывом всем им потребовалось одинаковое количество времени, чтобы размахивать ногой. шаг назад вперед.«Будь вы быстрым, медленным или промежуточным, время изменения положения конечности на максимальной скорости в основном одинаковое», — говорит он.
Усэйн Болт пересекает финишную черту и выигрывает золото в эстафете 4х100 метров на чемпионате мира по легкой атлетике ИААФ в Пекине в 2015 году. чтобы ноги двигались быстрее. Но это неправда. Так почему же Bolt разгоняется до максимальной скорости 27,8 миль в час, и у ваших ног возникает ощущение, что они вот-вот откажутся, как только вы пройдете немного выше пробежки?
чтобы ноги двигались быстрее. Но это неправда. Так почему же Bolt разгоняется до максимальной скорости 27,8 миль в час, и у ваших ног возникает ощущение, что они вот-вот откажутся, как только вы пройдете немного выше пробежки?
Все сводится к тому, насколько вы сильны.Чем выше сила удара при каждом ударе, тем выше бегун поднимается в воздух и тем дальше он проходит, прежде чем снова ударится по земле. Элитные бегуны на максимальной скорости на самом деле толкают около 1000 фунтов силы на шаг — это полтонны .
Здесь будет справедливо сделать шаг назад и задуматься, не все ли это сумасшедшие разговоры. Как снижение веса на может сделать вас быстрее ? И разве силовой бег не является противоположностью «легкого» аэродинамического качества, которое, кажется, поддерживают последние кроссовки? Разве мышцы ног, суставы и сухожилия не выходят из строя, если вы прикладываете к ним всю эту силу?
Это озадачило и команду Вейанда.Но исследование группы показало, что когда вы прыгаете вперед на одной ноге, сила удара при каждом приземлении примерно на треть сильнее, чем при спринте. Ноги бегунов могут требовать гораздо большей силы, чем мы думаем.
Ноги бегунов могут требовать гораздо большей силы, чем мы думаем.
Их останавливает время. Элитные спринтеры проводят столько же времени, сколько и вы, в воздухе на шаг, но меньше времени они проводят, фактически касаясь земли. В этом есть смысл — если Усэйн Болт движется вдвое быстрее, чем вы, то у него есть только половина времени, чтобы соединиться с землей, чем гусеница движется под его ногами.Таким образом, ему приходится оказывать гораздо большее давление, чем вам, с каждым ударом, но у него гораздо меньше времени, чтобы сделать это.
Этот является реальным ограничивающим фактором скорости человека — не само приложение давления, а скорость его применения. Болт исключителен не в своей способности махать ногами вперед и назад, а в его способности очень быстро бить по земле и отталкиваться от нее. Это ограничено временем реакции быстро сокращающихся мышечных волокон ноги.
Вейанд оценивает, что, если бы существовал какой-то способ повысить отзывчивость мышц ног до такой степени, что мы бежим до предела наших ног, чтобы поглотить удар, люди могли бы бегать со скоростью 40 миль в час или быстрее. Но это чисто теоретически; Дело в том, что до сих пор никто не придумал, как заставить ноги бить быстрее и сильнее, чем Усэйн Болт.
Но это чисто теоретически; Дело в том, что до сих пор никто не придумал, как заставить ноги бить быстрее и сильнее, чем Усэйн Болт.
Бесконечное количество переменных влияет на исход гонки. Getty Images / Майкл Стил
Но когда-нибудь кто-нибудь это сделает.
Есть так много разных способов вмешательства в поисках более высоких скоростей. Более разумные тренировки и питание — это одно, но есть также факторы, не связанные с телом, такие как кроссовки, стартовые блоки и материал для бега, которые имеют огромное значение.Они имеют очень мало общего с механикой или возможностями человеческого тела, но имеют огромное значение.
Пределы в основном определяются не нашими телами, и они также сильно зависят от параметров, которые мы устанавливаем, чтобы решить, какие виды вмешательства приемлемы для дальнейшего увеличения скорости человека. Вы побили рекорд скорости, сбежав с холма? Если бы ветер был тебе в спину? Если вы принимали препараты, улучшающие работоспособность? Если бы вы были созданы с помощью генной инженерии, чтобы наращивать более сильные и быстрые мышцы ног?
Weyand не видит будущего, в котором рекорды перестанут бить; существует слишком много разных способов юридически повлиять на производительность за счет лучшего обучения и лучших технологий. «Эти вмешательства становятся все более и более мощными и, вероятно, будут продолжать делать это, и они должны это сделать, если рекорды будут продолжать падать. Так что пока есть экономические стимулы, а наука и технологии движутся вперед, будут появляться все более и более действенные способы повышения производительности ».
«Эти вмешательства становятся все более и более мощными и, вероятно, будут продолжать делать это, и они должны это сделать, если рекорды будут продолжать падать. Так что пока есть экономические стимулы, а наука и технологии движутся вперед, будут появляться все более и более действенные способы повышения производительности ».
Скорость человека не ограничена. Нет нерушимого рекорда. Единственное ограничение — это ресурсы, которые мы готовы потратить, пытаясь их сломать.
Эффективность бега человека на основе больших данных реального мира
Универсальная модель производительности
В предыдущей работе мы разработали модель, которая может использоваться для извлечения показателей аэробной производительности из данных о гонках 14 . Подводя итог, можно сказать, что эта модель выражает интенсивность упражнений по шкале относительной мощности p , которая варьируется от нуля, соответствующего базовой скорости метаболизма, до единицы при генерации MAP. Ожидается, что MAP будет соответствовать максимальному поглощению кислорода VO 2, max , но эту аналогию не следует использовать в нашем подходе.Линейная зависимость p ( v ) отображает скорость бега v в относительную мощность с p ( v m ) = 1, определяя v m как индекс аэробной мощности, связанный с MAP за пределами который анаэробный источник энергии может дать p > 1 только в течение короткого времени. Анаэробная подача способствует максимальной нагрузке короче, чем время перехода t c , которое в нашей модели является самым длинным временем, в течение которого может поддерживаться САД.Важное предсказание нашей модели состоит в том, что максимальное значение относительной мощности p , которое может поддерживать бегун, логарифмически снижается с продолжительностью, со скоростью γ l , предполагая, что продолжительность больше, чем t c .
Ожидается, что MAP будет соответствовать максимальному поглощению кислорода VO 2, max , но эту аналогию не следует использовать в нашем подходе.Линейная зависимость p ( v ) отображает скорость бега v в относительную мощность с p ( v m ) = 1, определяя v m как индекс аэробной мощности, связанный с MAP за пределами который анаэробный источник энергии может дать p > 1 только в течение короткого времени. Анаэробная подача способствует максимальной нагрузке короче, чем время перехода t c , которое в нашей модели является самым длинным временем, в течение которого может поддерживаться САД.Важное предсказание нашей модели состоит в том, что максимальное значение относительной мощности p , которое может поддерживать бегун, логарифмически снижается с продолжительностью, со скоростью γ l , предполагая, что продолжительность больше, чем t c . Этот вывод согласуется с выводом А.В. Хилл, наблюдавший эту форму снижения мировых рекордов в беге 21 . Подробнее о нашей модели см. В разделе «Методы». Здесь мы используем это универсальное, т.е.е., субъектная независимая модель беговой производительности человека, чтобы извлечь индексы аэробной производительности из времени финиша бегунов по всему миру, сопоставив их с прогнозами модели 14 . Анализируемый набор данных поступает с платформы отслеживания упражнений, которая содержит точные записи о расстоянии и продолжительности (и, следовательно, средней скорости) беговой активности ≈19 тыс. Человек, которые пробежали в общей сложности 32 млн км за период 3,5 года. Данные были записаны людьми с помощью цифровых спортивных часов GPS (V800, Polar Electro Oy, Оулу, Финляндия) 25 и загружены на платформу.Максимальные результаты индивидуума измерялись самым быстрым временем финиша на четырех наиболее распространенных гоночных дистанциях 5000 м, 10000 м, полумарафоне (21 097,5 м) и марафоне (42 195 м) в течение гоночного сезона, который определяется как 180 дней.
Этот вывод согласуется с выводом А.В. Хилл, наблюдавший эту форму снижения мировых рекордов в беге 21 . Подробнее о нашей модели см. В разделе «Методы». Здесь мы используем это универсальное, т.е.е., субъектная независимая модель беговой производительности человека, чтобы извлечь индексы аэробной производительности из времени финиша бегунов по всему миру, сопоставив их с прогнозами модели 14 . Анализируемый набор данных поступает с платформы отслеживания упражнений, которая содержит точные записи о расстоянии и продолжительности (и, следовательно, средней скорости) беговой активности ≈19 тыс. Человек, которые пробежали в общей сложности 32 млн км за период 3,5 года. Данные были записаны людьми с помощью цифровых спортивных часов GPS (V800, Polar Electro Oy, Оулу, Финляндия) 25 и загружены на платформу.Максимальные результаты индивидуума измерялись самым быстрым временем финиша на четырех наиболее распространенных гоночных дистанциях 5000 м, 10000 м, полумарафоне (21 097,5 м) и марафоне (42 195 м) в течение гоночного сезона, который определяется как 180 дней. перед марафонским забегом (см. раздел «Методы» для определения гоночной активности).
перед марафонским забегом (см. раздел «Методы» для определения гоночной активности).
Скорость, соответствующая нашему параметру v m трудно измерить в лабораторных условиях, так как VO 2, max может быть достигнут в широком диапазоне субмаксимальных интенсивностей из-за дрейфа потребления кислорода вверх во время упражнений. Продолжительность 18,19 .В общем, наша модель может определить v m из пересечения соотношения гонка – время – расстояние в момент времени t c , и, следовательно, она свободна от этих сложностей. Самый простой вариант модели предполагает фиксированное время t c . Прогнозы модели для характеристик суб-MAP не зависят от этого фиксированного времени, поскольку другие варианты приводят только к последовательно перенормированным значениям для v m и γ l (которые в этом случае больше не связаны строго с MAP, а с немного другая мощность). В соответствии с применением нашей модели к текущим рекордам как для супер-, так и для суб-MAP ветвей 14 и лабораторных испытаний 26 , мы выбираем t c = 6 мин в следующем. Комбинируя экономию бега и снижение частичного использования максимальной выходной мощности с продолжительностью гонки, самое быстрое время T ( d ) на дистанции d дается универсальным выражением
В соответствии с применением нашей модели к текущим рекордам как для супер-, так и для суб-MAP ветвей 14 и лабораторных испытаний 26 , мы выбираем t c = 6 мин в следующем. Комбинируя экономию бега и снижение частичного использования максимальной выходной мощности с продолжительностью гонки, самое быстрое время T ( d ) на дистанции d дается универсальным выражением
$$ T (d) = — \ frac {{t} _ {\ text {c}}} {{\ gamma} _ {\ text {l}}} \ frac {d} {{d} _ {\ text {c}}} \ frac {1} {{W} _ {- 1} \ left [- \ frac {d} {{d} _ {\ text {c}}} \ frac {\ exp (-1 / {\ gamma} _ {\ текст {l}})} {{\ gamma} _ {\ text {l}}} \ right]} \ quad {\ rm {for}} \ \ d \ ge {d} _ {\ text {c}} \, $$
(1)
, где мы определили d c = v m t c , а W −1 является реальной ветвью функции Lambert W , которая определяется как многозначная обратная функция \ (w \ to w \ exp (w) \) 27 . W −1 ( z ) является действительным значением для −1 / e ≤ z <0, что выполняется для всех рассматриваемых нами расстояний d (см. Раздел «Методы» для более подробной информации. ). Обратите внимание, что T ( d c ) = t c , т. Е. d c — это расстояние, которое может быть пройдено максимально за время t c . Условие d ≥ d c всегда выполняется для рассматриваемых здесь гоночных дистанций.Отметим, что уравнение. (1) — точное решение нашей модели. Его также можно получить из более ранних описаний энергетики бега на выносливость 28,29,30 , когда дробное использование MAP описывается нашим предсказанием медленного, логарифмического распада и линейного увеличения затрат энергии на бег с предполагается скорость.
W −1 ( z ) является действительным значением для −1 / e ≤ z <0, что выполняется для всех рассматриваемых нами расстояний d (см. Раздел «Методы» для более подробной информации. ). Обратите внимание, что T ( d c ) = t c , т. Е. d c — это расстояние, которое может быть пройдено максимально за время t c . Условие d ≥ d c всегда выполняется для рассматриваемых здесь гоночных дистанций.Отметим, что уравнение. (1) — точное решение нашей модели. Его также можно получить из более ранних описаний энергетики бега на выносливость 28,29,30 , когда дробное использование MAP описывается нашим предсказанием медленного, логарифмического распада и линейного увеличения затрат энергии на бег с предполагается скорость.
Параметры модели, называемые индексами производительности, позволяют количественно оценить различные аспекты производительности и дают уникальное представление об основных детерминантах физической подготовки большой популяции бегунов в широком диапазоне физических нагрузок и в долгосрочной перспективе. Скорость v m измеряет комбинированную экономию бега и MAP и, как известно, лучше предсказывает производительность, чем VO 2, max отдельно 31 . Мы определяем индекс выносливости как \ ({E} _ {\ text {l}} = \ exp (0.1 / {\ gamma} _ {\ text {l}}) \), который кодирует 90% v м можно обслуживать в течение длительного времени E l t c > t c . Пара показателей производительности v m , E l достаточна для учета вариаций гоночной скорости на расстояниях от d c (обычно одна миля в нашем наборе данных) до марафона.Например, при анализе постоянных данных о беге отдельных людей мы обнаружили убедительные доказательства того, что они следуют тому же универсальному закону масштабирования, что и по формуле. (1) как работают мировые (или национальные) рекорды, со средними ошибками менее 1% 14 . Здесь оценки нашей модели основаны на самом быстром времени человека на четырех фиксированных дистанциях: 5 км, 10 км, полумарафон и марафон.
Скорость v m измеряет комбинированную экономию бега и MAP и, как известно, лучше предсказывает производительность, чем VO 2, max отдельно 31 . Мы определяем индекс выносливости как \ ({E} _ {\ text {l}} = \ exp (0.1 / {\ gamma} _ {\ text {l}}) \), который кодирует 90% v м можно обслуживать в течение длительного времени E l t c > t c . Пара показателей производительности v m , E l достаточна для учета вариаций гоночной скорости на расстояниях от d c (обычно одна миля в нашем наборе данных) до марафона.Например, при анализе постоянных данных о беге отдельных людей мы обнаружили убедительные доказательства того, что они следуют тому же универсальному закону масштабирования, что и по формуле. (1) как работают мировые (или национальные) рекорды, со средними ошибками менее 1% 14 . Здесь оценки нашей модели основаны на самом быстром времени человека на четырех фиксированных дистанциях: 5 км, 10 км, полумарафон и марафон. К сожалению, мы не можем определить из доступного набора данных, была ли производительность достигнута во время реальных гонок.Однако для нашего подхода требуется только, чтобы зарегистрированные характеристики соответствовали максимальному усилию на заданной дистанции бега, достигнутому в течение гоночного сезона.
К сожалению, мы не можем определить из доступного набора данных, была ли производительность достигнута во время реальных гонок.Однако для нашего подхода требуется только, чтобы зарегистрированные характеристики соответствовали максимальному усилию на заданной дистанции бега, достигнутому в течение гоночного сезона.
Данные об упражнениях
Обзор схемы анализа данных представлен на рис. 1. Все доступные предметы и действия в наборе данных платформы отслеживания упражнений были сгруппированы по SID и дате марафона, объединяя все индивидуальные беговые активности в течение 180 дней до марафона, определяя сезон.Для каждого сезона действия с лучшим временем на четырех фиксированных дистанциях определяли сезон гонок. Мы поставили условие, что в каждом гоночном сезоне должно быть не менее двух гонок. Если в сезоне было 30 или более занятий бегом, они определялись как тренировочный сезон. Для единообразия ко всем видам деятельности и гонкам были применены определенные фильтры данных (подробнее см. В разделе «Методы»). Были определены два варианта гоночного сезона, с включением и исключением марафона. Всего было проанализировано ~ 25 000 гоночных сезонов, включая марафон, и ~ 10 000 гоночных сезонов без марафона, и ~ 22 000 тренировочных сезонов (см. Таблицу 1, где приведены сводные данные и выполненный анализ).
В разделе «Методы»). Были определены два варианта гоночного сезона, с включением и исключением марафона. Всего было проанализировано ~ 25 000 гоночных сезонов, включая марафон, и ~ 10 000 гоночных сезонов без марафона, и ~ 22 000 тренировочных сезонов (см. Таблицу 1, где приведены сводные данные и выполненный анализ).
SID: идентификатор субъекта, M: марафон, M-дата: дата марафона, d: общая дистанция бега, «сезон забега»: лучшее время спортсмена по крайней мере на двух дистанциях 5 км, 10 км, половину дистанции. марафон и марафон (± 3% с учетом допуска GPS), N гонок : общее количество гонок, N M : количество успешных подгонок модели, N T : количество проанализированных сезоны тренировок, для которых можно было получить физиологические параметры v m , E l и спрогнозировать фактическое время гонок в пределах средней ошибки менее 5%, «полный тренировочный сезон»: не менее 30 занятий в течение 180 дней до начала соревнований. М-свидание.
М-свидание.
Точность прогноза производительности
Для всех людей мы оценили их показатели производительности v m и γ l для каждого гоночного сезона путем сопоставления гоночных событий с уравнением. (1) за счет минимизации относительной ошибки прогнозирования времени гонки. Плотности вероятности этих показателей показаны на рис. 2. Для всех гоночных сезонов с тремя и более гонками ( N = 12 309) средняя ошибка между прогнозом модели и фактическим временем гонки составляла всего 2.0%. Это говорит о том, что наша модель правильно отражает детерминанты аэробной выносливости. Корреляция между показателями результативности и временем финиша марафона представлена на рис. 3. Чтобы более подробно исследовать прогнозирующую способность нашей модели, мы применили нашу модель также к гоночному сезону, исключив результаты марафона (см. Рис. 4). Это позволило оценить время финиша марафона только по выступлениям на более коротких дистанциях. В зависимости от показателей производительности в наиболее вероятном диапазоне параметров модель предсказала результаты марафона с общей точностью лучше 10%.Только для очень малой (или большой) выносливости E l расчетное время, как правило, было слишком медленным (или быстрым), что указывает на то, что субмарафонские дистанции проходили непоследовательно, что привело к заниженной (или завышенной) оценке E л . Принимая во внимание все возможные неопределенности в марафонских гонках, которые находятся вне контроля данного исследования (например, погода, профиль трассы и мотивация спортсмена), наши прогнозы относительно времени финиша марафона весьма удовлетворительны.
Это позволило оценить время финиша марафона только по выступлениям на более коротких дистанциях. В зависимости от показателей производительности в наиболее вероятном диапазоне параметров модель предсказала результаты марафона с общей точностью лучше 10%.Только для очень малой (или большой) выносливости E l расчетное время, как правило, было слишком медленным (или быстрым), что указывает на то, что субмарафонские дистанции проходили непоследовательно, что привело к заниженной (или завышенной) оценке E л . Принимая во внимание все возможные неопределенности в марафонских гонках, которые находятся вне контроля данного исследования (например, погода, профиль трассы и мотивация спортсмена), наши прогнозы относительно времени финиша марафона весьма удовлетворительны.
Скорость кроссовера v m , которая является наименьшей скоростью, которая вызывает максимальную аэробную мощность MAP и выносливость E l получены путем применения нашей модели к самым быстрым характеристикам объекта на четырех дистанциях 5 км , 10 км, полумарафон и марафон гоночного сезона. Для этих распределений было проанализировано 24 858 гоночных сезонов. a Скорость v m приблизительно нормально распределена со средним значением 4.4 мс −1 . b Плотность вероятности выносливости E l напоминает экспоненциальный спад. c Плотность вероятности относительной мощности для 1 часа использования (1hU) достигает пика примерно на 82% от MAP.
Для этих распределений было проанализировано 24 858 гоночных сезонов. a Скорость v m приблизительно нормально распределена со средним значением 4.4 мс −1 . b Плотность вероятности выносливости E l напоминает экспоненциальный спад. c Плотность вероятности относительной мощности для 1 часа использования (1hU) достигает пика примерно на 82% от MAP.
a Визуализация времени марафонского забега T м в плоскости параметров ( v m , E l ).Показатели результативности получены на основе лучших результатов отдельных спортсменов в течение гоночного сезона. Цвет меняется с быстрого (пурпурный) на более медленный (синий) время окончания (время в минутах см. В цветовой легенде). Пары параметров ( v м , E l ) вдоль пунктирных кривых дают одинаковое время марафонской гонки, указанное в верхней части графика (в формате чч: мм). b Цветная визуализация числа n гоночных сезонов, анализируемых как функция параметров ( v m , E l ).
Пары параметров ( v м , E l ) вдоль пунктирных кривых дают одинаковое время марафонской гонки, указанное в верхней части графика (в формате чч: мм). b Цветная визуализация числа n гоночных сезонов, анализируемых как функция параметров ( v m , E l ).
a Визуализация относительной разницы Δ T м между фактическим и расчетным временем марафонского забега T м (в процентах от времени забега) в зависимости от скорости кроссовера v м и выносливость E л . Пурпурный (синий) цвет указывает на более быструю (более медленную) отделку, чем предполагалось. b Плотность вероятности различий во времени гонок, обозначенная цветом в соответствии с группами различных временных интервалов гонок.
Максимальная скорость в течение 1 часа
Анализ ~ 25 000 гоночных сезонов показывает нормально распределенную скорость v m и экспоненциальный спад плотности вероятности для выносливости E l (см. Рис. 2). Интересно, что VO 2, max в исследовании 450 элитных футболистов также подчиняется нормальному распределению 32 . Обратите внимание, что v m также измеряет экономичность бега, которая значительно различается у разных людей и регулирует производительность 24 .В физиологии упражнений способность бегуна поддерживать определенное усилие часто характеризуется пороговыми значениями, частым примером которых является порог лактата. В нашем подходе, однако, существует постоянная связь между выходной мощностью и скоростью, и изменение этой связи с продолжительностью кажется естественной мерой выносливости. Следовательно, в качестве практической меры выносливости мы определяем в нашей модели скорость \ ({v} _ {\ text {1hU}} = {v} _ {\ text {m}} [1-0. 1 \, \ mathrm { log} \, (60 \ min / {t} _ {\ text {c}}) / \ mathrm {log} \, ({E} _ {\ text {l}})] \), которые бегун может поддерживать в течение 1 часа, что соответствует максимальному дробному использованию MAP в течение 1 часа.Хотя здесь можно выбрать любую продолжительность, мы использовали 1 час по аналогии с тренерами по бегу, определяя пороговую скорость как усилие, которое можно поддерживать в течение примерно 1 часа 33 . Коэффициент использования за 1 час p 1hU = v 1hU / v m был оценен ранее на основе лабораторных измерений и забегов для небольшой группы из 18 бегунов на длинные дистанции мужского пола и составлял примерно 0,82 ± 0,05 34 . Поразительно, но наши результаты, полученные на основе текущих данных для ~ 14000 субъектов, подтверждают этот диапазон без каких-либо инвазивных измерений, как показано на рис.2c. Более того, наше наблюдение экспоненциально малой, но конечной вероятности для больших E l объясняет наблюдаемые значения p 1hU ≈0.
1 \, \ mathrm { log} \, (60 \ min / {t} _ {\ text {c}}) / \ mathrm {log} \, ({E} _ {\ text {l}})] \), которые бегун может поддерживать в течение 1 часа, что соответствует максимальному дробному использованию MAP в течение 1 часа.Хотя здесь можно выбрать любую продолжительность, мы использовали 1 час по аналогии с тренерами по бегу, определяя пороговую скорость как усилие, которое можно поддерживать в течение примерно 1 часа 33 . Коэффициент использования за 1 час p 1hU = v 1hU / v m был оценен ранее на основе лабораторных измерений и забегов для небольшой группы из 18 бегунов на длинные дистанции мужского пола и составлял примерно 0,82 ± 0,05 34 . Поразительно, но наши результаты, полученные на основе текущих данных для ~ 14000 субъектов, подтверждают этот диапазон без каких-либо инвазивных измерений, как показано на рис.2c. Более того, наше наблюдение экспоненциально малой, но конечной вероятности для больших E l объясняет наблюдаемые значения p 1hU ≈0. 9 у некоторых хорошо подготовленных бегунов на длинные дистанции.
9 у некоторых хорошо подготовленных бегунов на длинные дистанции.
Мы также вычислили время марафона на основе нашей модели и сравнили его с фактическим временем марафона T м для всех гоночных сезонов, см. Рис. 3. Наша модель предсказывает теоретические кривые постоянной T м дюйма плоскость показателей эффективности (показаны пунктирными линиями на рис.3а). Мы обнаружили, что фактическое время гонок упорядочено в соответствии с этими кривыми. Это показывает, что выбранные нами физиологические профили, рассчитанные на основе лучших результатов субмарафона и марафона, сильно коррелируют с T m . Важно понимать, что место результатов марафона в пространстве параметров определяется всеми гонками и, следовательно, отражает относительную важность индексов v m и E l . Это демонстрирует решающую важность учета выносливости в дополнение к MAP и экономии бега при оценке результатов бегунов на длинные дистанции.
Важность выносливости
Наши результаты демонстрируют сильную чувствительность производительности к выносливости. Например, бегун со скоростью v м = 5 м с −1 может улучшить свое марафонское время с 3 часов 27 минут 38 секунд до 2 часов 53 минут 8 секунд, удвоив выносливость с E. l = от 3 до E l = 6 (соответствует изменению одночасового использования с 79 до 87% от VO 2max ), без каких-либо изменений VO 2, max или работает экономия.Мы также обнаружили, что более быстрые бегуны, как правило, бегают более последовательно на всех дистанциях, чем более медленные бегуны, на что указывает зависимость ошибки прогноза Δ T m от времени финиша марафона (см. Рис. 4b). Например, в нашей группе самых быстрых бегунов со временем марафона менее 160 минут ошибка прогноза обычно составляла менее ± 2,5%. Это наблюдение подтверждает наше объяснение наблюдаемой неопределенности параметра выносливости E l .
Корреляция с тренировками
Наконец, мы сравнили физиологические профили с беговой активностью в течение тренировочного сезона. Существует несколько исследований взаимосвязи между тренировочным объемом и интенсивностью, улучшением аэробной формы и производительности 35 . Например, было заявлено, что бег со скоростью v m может представлять собой оптимальный стимул для повышения выносливости 36 . Есть также свидетельства, подтверждающие, что относительно большой процент низкоинтенсивных тренировок в течение длительного периода улучшает производительность во время высокоинтенсивных тренировок на выносливость 37,38 .Утверждалось, что скорость бега на пороге лактата является лучшим физиологическим показателем эффективности бега на длинные дистанции. 39 .
Чтобы исследовать влияние тренировочной дистанции и скорости по отношению к скорости v m , мы выбрали последовательные сезоны гонок, определяемые тем, что средняя ошибка прогнозирования времени гонки составляет менее 5%. Рисунок 5a показывает, что по мере увеличения общего тренировочного расстояния d train за тренировочный сезон, v m увеличивается в среднем линейно, со слабой тенденцией насыщения на самом большом d train .Несколько исследований продемонстрировали увеличение против м за счет тренировки на выносливость 35 . Более высокая скорость v m может быть достигнута за счет большей экономичности хода и / или увеличения MAP. Мы предполагаем, что более длинные дистанции тренировки улучшили экономичность бега, что согласуется с предыдущими наблюдениями в группе из одиннадцати хорошо подготовленных бегунов на длинные дистанции 40 . Наш анализ обеспечивает статистически значимую количественную связь между тренировочной дистанцией и скоростью в MAP, v m , для ~ 22 000 тренировочных сезонов.Другое объяснение этой связи может заключаться в том, что более подготовленные бегуны с большим MAP и, следовательно, более высоким v m увеличивают километраж во время тренировки.
Рисунок 5a показывает, что по мере увеличения общего тренировочного расстояния d train за тренировочный сезон, v m увеличивается в среднем линейно, со слабой тенденцией насыщения на самом большом d train .Несколько исследований продемонстрировали увеличение против м за счет тренировки на выносливость 35 . Более высокая скорость v m может быть достигнута за счет большей экономичности хода и / или увеличения MAP. Мы предполагаем, что более длинные дистанции тренировки улучшили экономичность бега, что согласуется с предыдущими наблюдениями в группе из одиннадцати хорошо подготовленных бегунов на длинные дистанции 40 . Наш анализ обеспечивает статистически значимую количественную связь между тренировочной дистанцией и скоростью в MAP, v m , для ~ 22 000 тренировочных сезонов.Другое объяснение этой связи может заключаться в том, что более подготовленные бегуны с большим MAP и, следовательно, более высоким v m увеличивают километраж во время тренировки. К сожалению, мы не смогли измерить v m в начале и в конце тренировочного сезона независимо от двух разных гоночных сезонов или испытаний на время. Мы также обнаружили линейное уменьшение против м со средней относительной интенсивностью тренировки от 50% до примерно 90% от против м , как показано на рис.5б. Наши результаты можно интерпретировать как более быстрые бегуны, как правило, с более низкой относительной интенсивностью, что согласуется с улучшением результатов при высокой интенсивности за счет тренировок с низкой интенсивностью. Диапазон тренировочных скоростей увеличивается с увеличением v m , что отражает более широкий диапазон доступных интенсивностей от минимальной (бег трусцой) до максимальной скорости. Например, бегун с v м = 4 м с −1 обычно (в пределах одного стандартного отклонения) тренирует от 64 до 84% от v м или MAP, а бегун с v м = 5 м с −1 обычно составляет до 66% от v м , так что оба бегуна имеют почти одинаковый верхний темп ~ 5 мин.
К сожалению, мы не смогли измерить v m в начале и в конце тренировочного сезона независимо от двух разных гоночных сезонов или испытаний на время. Мы также обнаружили линейное уменьшение против м со средней относительной интенсивностью тренировки от 50% до примерно 90% от против м , как показано на рис.5б. Наши результаты можно интерпретировать как более быстрые бегуны, как правило, с более низкой относительной интенсивностью, что согласуется с улучшением результатов при высокой интенсивности за счет тренировок с низкой интенсивностью. Диапазон тренировочных скоростей увеличивается с увеличением v m , что отражает более широкий диапазон доступных интенсивностей от минимальной (бег трусцой) до максимальной скорости. Например, бегун с v м = 4 м с −1 обычно (в пределах одного стандартного отклонения) тренирует от 64 до 84% от v м или MAP, а бегун с v м = 5 м с −1 обычно составляет до 66% от v м , так что оба бегуна имеют почти одинаковый верхний темп ~ 5 мин. Км −1 для большинства их пробегов.Медленные бегуны должны тренироваться с относительно высокой интенсивностью, если они хотят избежать перехода к ходьбе. Важно понимать, что эти типичные диапазоны не включают быстрые высокоинтенсивные тренировки, на которые приходится лишь небольшая часть общего тренировочного объема. Однако сеансы высокой интенсивности включают также фазы отдыха, которые могут снизить среднюю скорость, когда таймер не остановлен, что потенциально объясняет наблюдаемую интенсивность ниже ~ 50% от v m .
Км −1 для большинства их пробегов.Медленные бегуны должны тренироваться с относительно высокой интенсивностью, если они хотят избежать перехода к ходьбе. Важно понимать, что эти типичные диапазоны не включают быстрые высокоинтенсивные тренировки, на которые приходится лишь небольшая часть общего тренировочного объема. Однако сеансы высокой интенсивности включают также фазы отдыха, которые могут снизить среднюю скорость, когда таймер не остановлен, что потенциально объясняет наблюдаемую интенсивность ниже ~ 50% от v m .
Мы измерили расстояние и время для каждого бегового упражнения во время тренировочного сезона для 21 605 сезонов. На графиках показаны наблюдаемые отношения между показателями производительности (полученные на основе модели, соответствующей сезону гонок) и различными показателями тренировочного объема и интенсивности. Пурпурная линия указывает среднее значение, серая область — одно стандартное отклонение, а светло-пурпурная и синяя заштрихованные области представляют стандартную ошибку среднего и стандартного отклонения, соответственно, полученные в результате повторной выборки бутстрапов с заменой (см. Раздел «Методы» для получения дополнительной информации Детали). a Увеличение скорости перехода v м с общей дистанцией d поезд тренировочных заездов. b Связь между скоростью кроссовера v m и относительной интенсивностью тренировки \ ({p} _ {{\ rm {train}}} = {\ bar {v}} _ {{\ rm {train}}} / {v} _ {\ text {m}} \) где \ ({\ bar {v}} _ {{\ rm {train}}} \) — средняя скорость обучения. c Повышение и насыщение выносливости E l с тренировочным импульсом (TRIMP). d Экспоненциальный рост выносливости E l при относительной интенсивности тренировок.
Пурпурная линия указывает среднее значение, серая область — одно стандартное отклонение, а светло-пурпурная и синяя заштрихованные области представляют стандартную ошибку среднего и стандартного отклонения, соответственно, полученные в результате повторной выборки бутстрапов с заменой (см. Раздел «Методы» для получения дополнительной информации Детали). a Увеличение скорости перехода v м с общей дистанцией d поезд тренировочных заездов. b Связь между скоростью кроссовера v m и относительной интенсивностью тренировки \ ({p} _ {{\ rm {train}}} = {\ bar {v}} _ {{\ rm {train}}} / {v} _ {\ text {m}} \) где \ ({\ bar {v}} _ {{\ rm {train}}} \) — средняя скорость обучения. c Повышение и насыщение выносливости E l с тренировочным импульсом (TRIMP). d Экспоненциальный рост выносливости E l при относительной интенсивности тренировок.
Оптимальный тренировочный импульс
Мы обнаружили убедительные доказательства того, что комбинированный эффект тренировочного объема и интенсивности, известный как TRaining IMPulse (TRIMP) 41 , увеличивает выносливость только до предела. Ранее было обнаружено, что у бегунов-любителей на длинные дистанции индивидуальный TRIMP коррелирует с результатами бега на 5000 и 10000 м 42 . Мы вычислили TRIMP, суммируя очки TRIMP за все серии тренировочного сезона.Для каждого прогона баллы TRIMP присваивались в соответствии с продолжительностью забега и его относительной средней скоростью \ (\ bar {v} / {v} _ {\ text {m}} \) (подробности см. В разделе «Методы») . Мы проанализировали количественную связь между выносливостью E l и общим TRIMP за тренировочный сезон (см. Рис. 5c). Мы наблюдали начальное линейное увеличение E l с TRIMP, плато около E l = 7,5 ± 2 для TRIMP ~ 25000 и статистически значимое окончательное падение, которое может быть связано с перетренированием.Этот результат предполагает, что существует оптимальный TRIMP для тренировочного сезона, а соответствующая максимальная выносливость обеспечивает близкое к оптимальному время марафонского забега для данной скорости v m (см.
Ранее было обнаружено, что у бегунов-любителей на длинные дистанции индивидуальный TRIMP коррелирует с результатами бега на 5000 и 10000 м 42 . Мы вычислили TRIMP, суммируя очки TRIMP за все серии тренировочного сезона.Для каждого прогона баллы TRIMP присваивались в соответствии с продолжительностью забега и его относительной средней скоростью \ (\ bar {v} / {v} _ {\ text {m}} \) (подробности см. В разделе «Методы») . Мы проанализировали количественную связь между выносливостью E l и общим TRIMP за тренировочный сезон (см. Рис. 5c). Мы наблюдали начальное линейное увеличение E l с TRIMP, плато около E l = 7,5 ± 2 для TRIMP ~ 25000 и статистически значимое окончательное падение, которое может быть связано с перетренированием.Этот результат предполагает, что существует оптимальный TRIMP для тренировочного сезона, а соответствующая максимальная выносливость обеспечивает близкое к оптимальному время марафонского забега для данной скорости v m (см. Рис. 3a). Наконец, мы исследовали определение самого TRIMP, чтобы определить, реализует ли он наилучшее соотношение между выносливостью и интенсивностью тренировки. Мы обнаружили поразительное совпадение экспоненциальной зависимости E l от \ ({\ bar {v}} _ {{\ rm {train}}} / {v} _ {\ text {m}} \) и исходное определение TRIMP, основанное на повышении уровня лактата в крови с интенсивностью, как показано на рис.5г. Наши результаты для тысяч бегунов показывают, что отношения между режимом тренировки и показателями производительности, которые обычно доступны только при инвазивном и ресурсоемком лабораторном тестировании, могут быть надежно получены на основе данных о беговой активности.
Рис. 3a). Наконец, мы исследовали определение самого TRIMP, чтобы определить, реализует ли он наилучшее соотношение между выносливостью и интенсивностью тренировки. Мы обнаружили поразительное совпадение экспоненциальной зависимости E l от \ ({\ bar {v}} _ {{\ rm {train}}} / {v} _ {\ text {m}} \) и исходное определение TRIMP, основанное на повышении уровня лактата в крови с интенсивностью, как показано на рис.5г. Наши результаты для тысяч бегунов показывают, что отношения между режимом тренировки и показателями производительности, которые обычно доступны только при инвазивном и ресурсоемком лабораторном тестировании, могут быть надежно получены на основе данных о беговой активности.
Оптимальная скорость бега, связанная с эволюцией ранних стратегий охоты человека — ScienceDaily
Бегуны, слушайте: если ваше тело говорит вам, что ваш темп кажется слишком быстрым или слишком медленным, это может быть правильно.
Новое исследование, опубликованное 18 марта в журнале Journal of Human Evolution , показывает, что эффективность бега человека зависит от скорости и что у каждого человека есть оптимальный темп, в котором он или она может преодолеть наибольшее расстояние с наименьшими усилиями. .
.
Результат развенчивает давнее представление о том, что бег имеет одинаковые метаболические затраты на единицу времени независимо от скорости — другими словами, что энергия, необходимая для пробега заданной дистанции, одинакова как при беге, так и при беге трусцой. Хотя в краткосрочной перспективе спринт кажется более требовательным, более длительное время и постоянные нагрузки, необходимые для преодоления установленного расстояния в более медленном темпе, должны были уравновесить разницу в метаболических затратах, — говорит Карен Штудель, профессор зоологии из Университета Висконсина. Мэдисон.
Тем не менее, Steudel и Cara Wall-Scheffler из Тихоокеанского университета Сиэтла показали, что энергетические потребности бега меняются с разной скоростью. «Это означает, что существует оптимальная скорость, которая доставит вас туда с наименьшими затратами», — говорит Штудель.
Пиковая эффективность была определена путем измерения скорости метаболизма бегунов в диапазоне скоростей, обеспечиваемых моторизованной беговой дорожкой. Затраты на метаболическую энергию увеличивались как на быстрой, так и на медленной скорости и показали промежуточный темп максимальной эффективности.
Затраты на метаболическую энергию увеличивались как на быстрой, так и на медленной скорости и показали промежуточный темп максимальной эффективности.
Наиболее эффективная скорость бега, определенная в исследовании, варьировалась между людьми, но в среднем составляла около 8,3 мили в час для мужчин и 6,5 миль в час для женщин в группе из девяти опытных бегунов-любителей. По словам Штуделя, большая часть гендерных различий может быть связана с различиями в размере тела и длине ног, которые, как было показано, влияют на механику бега. В целом, у более крупных и высоких бегунов оптимальная скорость была выше.
Интересно, что самые медленные скорости — около 4.5 миль в час, или примерно 13-минутная миля — были наименее эффективными с точки зрения метаболизма, что Штудель связывает с переходом походки между ходьбой и бегом. Например, отмечает она, и очень быстрая ходьба, и очень медленный бег могут вызывать физический дискомфорт.
Вызывая большой интерес у спортсменов и тренеров, механика бега может также дать ключ к разгадке эволюции современной формы человеческого тела: высокого и длинноногого, с широкой грудью и четко очерченной талией.
Современные люди очень умело ходят и довольно хорошо бегают, говорит Стейдель, а эффективное передвижение, вероятно, давало нашим предкам преимущество при охоте и собирании пищи.У далеких предков, австралопитеков, было более короткое, квадратное телосложение с более короткими ногами.
«У них не было бы заметной талии — их торс больше походил на туловище обезьяны, за исключением того, что они ходили на двух ногах», — говорит Штудель. «С родом Homo вы начинаете становиться более высокими и крупными людьми, и они начали развивать более линейную форму тела» с отчетливыми поясами, которые легко поворачиваются, позволяя делать более длинные и эффективные шаги.
Также известно, что ходьба человека имеет оптимально эффективную скорость, поэтому новые открытия могут помочь исследователям определить относительную важность различных походок в развитии человека, говорит Стейдель.»Это часть вопроса о том, была ли ходьба или бег более важна в эволюции формы тела представителей рода Homo.
границ | Влияние скорости опорно-двигательного аппарата на кинематику плюснефалангового сустава человека
Введение
Передвижение человека включает интенсивное использование стоп для смягчения ударов о землю, поддержания стабильности опорно-двигательного аппарата, создания движущей силы во всем диапазоне скорости движения (Ker et al., 1987; Carrier et al., 1994; Ren et al., 2008a; Головка, Либерман, 2018). По-видимому, разные паттерны активации мышц стопы наблюдались с увеличением скорости движения от ходьбы к бегу (Mann and Hagy, 1979; Minetti et al., 1994; Srinivasan and Ruina, 2006; Lipfert et al., 2012), что приводит к различным картина силы реакции земли (GRF) при ходьбе во время бега (Cavanagh and Lafortune, 1980; Nilsson and Thorstensson, 1987, 1989). Также было обнаружено, что кинетика и кинематика голеностопного сустава и стопы во время ходьбы отличались от таковых во время бега на протяжении фазы опоры (Czerniecki, 1988; Rodgers, 1988; Holowka, Lieberman, 2018). Большинство предыдущих исследований локомоторной биомеханики стопы сосредоточены на сегменте стопы в целом и / или голеностопном суставе (Adelaar, 1986; Apkarian et al., 1989; Scott, Winter, 1993; Gefen et al., 2000; Carson et al., ., 2001; Nester et al., 2007; Altman, Davis, 2012). Тем не менее, плюснефаланговый сустав человека (МП), расположенный на самом дистальном конце сегмента стопы, также может играть важную роль (Bojsen-Møller and Lamoreux, 1979; Mann and Hagy, 1979; Stefanyshyn and Nigg, 1997; Kim et al. ., 2012).
Большинство предыдущих исследований локомоторной биомеханики стопы сосредоточены на сегменте стопы в целом и / или голеностопном суставе (Adelaar, 1986; Apkarian et al., 1989; Scott, Winter, 1993; Gefen et al., 2000; Carson et al., ., 2001; Nester et al., 2007; Altman, Davis, 2012). Тем не менее, плюснефаланговый сустав человека (МП), расположенный на самом дистальном конце сегмента стопы, также может играть важную роль (Bojsen-Møller and Lamoreux, 1979; Mann and Hagy, 1979; Stefanyshyn and Nigg, 1997; Kim et al. ., 2012).
Во время ходьбы человека подошвенная фасция постепенно растягивается вверх за счет тыльного сгибания плюснефалангового сустава, чтобы обернуть вокруг головок плюсневых костей (Ker et al., 1987; Fuller, 2000). Соответственно, это действие приводит к некоторому возвышению продольной дуги и дальнейшей стабилизации стопы без каких-либо мышечных воздействий, используя лебедочный механизм подошвенного апоневроза (Mann and Hagy, 1979; Fuller, 2000). Моментное плечо силы реакции опоры может быть сокращено за счет тыльного сгибания MP-сустава в фазе поздней стойки, действующего как жесткий рычаг ступни. Вероятно, эффективное механическое преимущество (EMA) тыльных мышц голеностопного сустава будет увеличено и, таким образом, уменьшится мышечное усилие во время отталкивания (Bojsen-Møller and Lamoreux, 1979; Biewener, 1989). Кроме того, тыльное сгибание сустава MP может помочь ограничить относительные движения кожи для передачи сил сдвига к скелету за счет сжатия системы соединительной ткани в стопе (Bojsen-Møller and Lamoreux, 1979; Vereecke and Aerts, 2008).
Вероятно, эффективное механическое преимущество (EMA) тыльных мышц голеностопного сустава будет увеличено и, таким образом, уменьшится мышечное усилие во время отталкивания (Bojsen-Møller and Lamoreux, 1979; Biewener, 1989). Кроме того, тыльное сгибание сустава MP может помочь ограничить относительные движения кожи для передачи сил сдвига к скелету за счет сжатия системы соединительной ткани в стопе (Bojsen-Møller and Lamoreux, 1979; Vereecke and Aerts, 2008).
Когда пальцы ног выдвигаются, чтобы уравновесить тело во время быстро меняющихся движений (Mann and Hagy, 1979; Holowka and Lieberman, 2018).Человеческий MP-сустав, возможно, играет важную роль в быстрых движениях тела, таких как бег. Одно исследование показало, что сустав МП действует как впечатляющий рассеиватель энергии во время спринта, который поглощает больше энергии при увеличении скорости (Стефанишин и Нигг, 1997). Ограниченное тыльное сгибание MP-сустава может привести к недостаточной выработке энергии во время отталкивания (Stefanyshyn and Nigg, 1997). Более того, в литературе сообщается, что голеностопный сустав, а также MP-сустав могут обеспечивать механизм переменной передачи (Carrier et al., 1994) тыльных мышц голеностопного сустава во время бега. Это может улучшить двигательные характеристики во время позднего бега, поддерживая работу мышц в высокоэффективной области кривой сила-скорость.
Более того, в литературе сообщается, что голеностопный сустав, а также MP-сустав могут обеспечивать механизм переменной передачи (Carrier et al., 1994) тыльных мышц голеностопного сустава во время бега. Это может улучшить двигательные характеристики во время позднего бега, поддерживая работу мышц в высокоэффективной области кривой сила-скорость.
MP-сустав человека был упрощен до единственной оси, исходящей из головки пятой плюсневой кости и перпендикулярной сагиттальной плоскости во многих исследованиях (Stefanyshyn and Nigg, 1997, 1998; Kim et al., 2012). Хотя движение сустава MP упрощено, это двумерное предположение не выражает наклонного характера.Одно исследование объяснило влияние различных определений осей суставов MP на расчетные переменные кинетики суставов при спринте с помощью обратной динамики (Smith et al., 2012). Результат показал, что определение оси шарнира MP существенно влияет на расчетный момент, мощность и энергию шарнира. Упрощенное двухмерное определение оси сустава может привести к большему поглощению энергии в MP-суставе, чем в наклонных осях сустава. Это предполагает, что представление сустава MP в подходящей форме имеет решающее значение для лучшего понимания функции сустава MP во время движения (Smith et al., 2012). Но почти во всех предыдущих исследованиях использовались упрощенные определения МП сустава исключительно на основе анатомических ориентиров на стопе, например, прямой линии, соединяющей 1-ю и 5-ю плюсневые головки (Bojsen-Møller and Lamoreux, 1979; Smith et al., 2012; Зелик и др., 2015). До сих пор трехмерная ориентация и положение фактической функциональной оси вращения МП-сустава во время передвижения человека и то, как оно изменяется при различных скоростях движения, не были тщательно изучены.В нашем последнем исследовании положение и ориентация функциональной оси (ФА) были определены при ходьбе с различной скоростью (Raychoudhury et al., 2014). Было обнаружено, что FA показывает статически отличное положение и ориентацию от анатомической оси (AA), которая определяется как прямая линия, соединяющая первую и пятую плюсневые головки, а скорость ходьбы оказывает статически значимое влияние на положения функциональной оси.
Это предполагает, что представление сустава MP в подходящей форме имеет решающее значение для лучшего понимания функции сустава MP во время движения (Smith et al., 2012). Но почти во всех предыдущих исследованиях использовались упрощенные определения МП сустава исключительно на основе анатомических ориентиров на стопе, например, прямой линии, соединяющей 1-ю и 5-ю плюсневые головки (Bojsen-Møller and Lamoreux, 1979; Smith et al., 2012; Зелик и др., 2015). До сих пор трехмерная ориентация и положение фактической функциональной оси вращения МП-сустава во время передвижения человека и то, как оно изменяется при различных скоростях движения, не были тщательно изучены.В нашем последнем исследовании положение и ориентация функциональной оси (ФА) были определены при ходьбе с различной скоростью (Raychoudhury et al., 2014). Было обнаружено, что FA показывает статически отличное положение и ориентацию от анатомической оси (AA), которая определяется как прямая линия, соединяющая первую и пятую плюсневые головки, а скорость ходьбы оказывает статически значимое влияние на положения функциональной оси.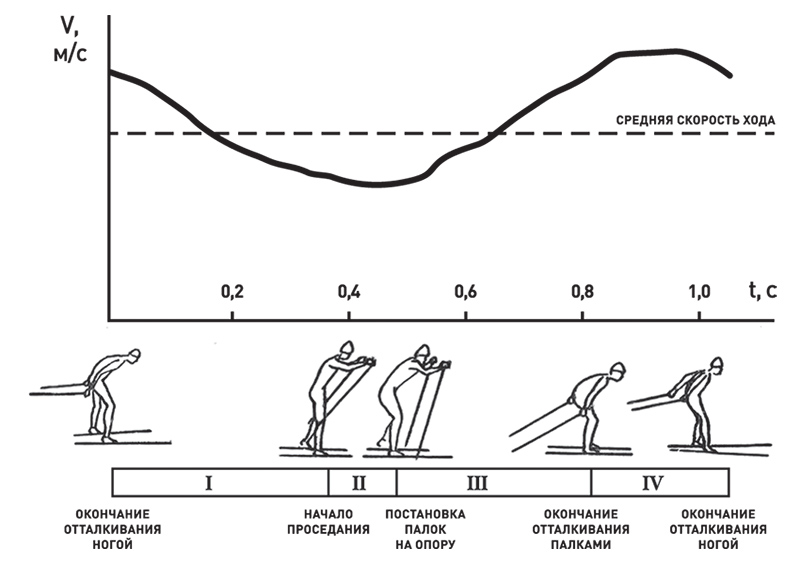
Эта статья направлена на продолжение нашего предыдущего исследования по изучению влияния скорости локомоторного движения на кинематику суставов МП человека.Положение и ориентация оси FA шарнира MP в фазе стояния при беге с разными скоростями определялись системой 3D-захвата движения. Статистический анализ был проведен для оценки разницы между функциональной осью MP-сустава человека и анатомической осью, обычно используемой в литературе. Кроме того, путем интеграции с набором данных о ходьбе, полученным в нашем предыдущем исследовании, было статистически проанализировано влияние скорости локомоторного движения на ориентацию и положение MP-сустава человека.Это дополнительно раскрыло бы механизм, лежащий в основе функции сустава МП, а также движение стопы во время движения с различными скоростями.
Материалы и методы
Измерение походки
Процедура эксперимента была такой же, как и в нашем предыдущем исследовании (Raychoudhury et al., 2014). Шесть здоровых взрослых людей с нормальной стопой ( N = 6, все мужчины; возраст 26,67 ± 2,69 года; масса 67,17 ± 10,29 кг; рост 1,75 ± 0,04 м; среднее значение ± стандартное отклонение), без предшествующей истории болезни с травмами нижней конечности и стопы , участвовал в этом исследовании. Эти шесть участников были теми же субъектами, которые участвовали в испытаниях по ходьбе (Raychoudhury et al., 2014). Основная причина брать одних и тех же испытуемых — статистическое сравнение результатов бега с ходьбой. Этим субъектам было предварительно предоставлено письменное информированное согласие перед участием и отдельно предоставлено письменное согласие в соответствии с политикой этического комитета университета. Им было предложено бегать босиком по дорожке с выбранным пользователем медленным (2,51 ± 0,26 м / с), нормальным (3.12 ± 0,22 м / с) и быстрой (4,14 ± 0,65 м / с) скоростью. Такая же система маркеров была установлена на правой ноге для записи относительного движения стопы. Трехмерные сегментарные движения измерялись с помощью двенадцати инфракрасной трехмерной системы захвата движения (Qualisys, Швеция) на частоте 150 Гц. GRF и момент измерялись на частоте 1000 Гц с помощью набора пластин из шести сил (Kistler, Швейцария) только для определения цикла походки. Процесс калибровки был таким же, как и при ходьбе (Raychoudhury et al.
Эти шесть участников были теми же субъектами, которые участвовали в испытаниях по ходьбе (Raychoudhury et al., 2014). Основная причина брать одних и тех же испытуемых — статистическое сравнение результатов бега с ходьбой. Этим субъектам было предварительно предоставлено письменное информированное согласие перед участием и отдельно предоставлено письменное согласие в соответствии с политикой этического комитета университета. Им было предложено бегать босиком по дорожке с выбранным пользователем медленным (2,51 ± 0,26 м / с), нормальным (3.12 ± 0,22 м / с) и быстрой (4,14 ± 0,65 м / с) скоростью. Такая же система маркеров была установлена на правой ноге для записи относительного движения стопы. Трехмерные сегментарные движения измерялись с помощью двенадцати инфракрасной трехмерной системы захвата движения (Qualisys, Швеция) на частоте 150 Гц. GRF и момент измерялись на частоте 1000 Гц с помощью набора пластин из шести сил (Kistler, Швейцария) только для определения цикла походки. Процесс калибровки был таким же, как и при ходьбе (Raychoudhury et al. , 2014). Cappozzo et al.(1995) предположили, что если анатомические ориентиры на кости можно было измерить напрямую (например, интракортикальные маркеры, просверленные в костях, или двухплоскостная рентгеновская система), соответствующие параметры калибровки будут легко доступны. В противном случае, если маркеры прикреплены к коже (в этой статье), следует провести процедуру калибровки (CAST). При каждом условии различной скорости бега репрезентативные данные бега были обеспечены повторением 15 раз измерения походки.
, 2014). Cappozzo et al.(1995) предположили, что если анатомические ориентиры на кости можно было измерить напрямую (например, интракортикальные маркеры, просверленные в костях, или двухплоскостная рентгеновская система), соответствующие параметры калибровки будут легко доступны. В противном случае, если маркеры прикреплены к коже (в этой статье), следует провести процедуру калибровки (CAST). При каждом условии различной скорости бега репрезентативные данные бега были обеспечены повторением 15 раз измерения походки.
Определение параметров сустава
Вся нижняя конечность была разделена на пять жестких сегментов: фаланги, предплюсны, голень, бедро и таз согласно литературным данным (Kim et al., 2012; Zelik et al., 2015; Holowka, Lieberman, 2018). Анатомическая система координат для каждого упомянутого сегмента была определена на основе предыдущих исследований (Ren et al., 2008a, 2010). Для этого исследования было сделано несколько предположений. Во-первых, пять фаланг образуют единый жесткий сегмент, хотя во время движения между фалангами происходят относительные движения. Во-вторых, шарнир MP считался одношарнирным. Как показано на Рисунке 1A, AA была описана как линия, соединяющая 1-ю и 5-ю плюсневые головки, а функциональная ось была определена как ось вращения между задним и передним отделом стопы, с более подробной информацией, описанной в Raychoudhury et al. (2014). Алгоритм закрытой формы (Gamage and Lasenby, 2002) был принят для оценки трехмерного положения и ориентации функциональной оси.
Во-вторых, шарнир MP считался одношарнирным. Как показано на Рисунке 1A, AA была описана как линия, соединяющая 1-ю и 5-ю плюсневые головки, а функциональная ось была определена как ось вращения между задним и передним отделом стопы, с более подробной информацией, описанной в Raychoudhury et al. (2014). Алгоритм закрытой формы (Gamage and Lasenby, 2002) был принят для оценки трехмерного положения и ориентации функциональной оси.
Рисунок 1. Определение параметров соединения МП. (A) Анатомическая ось (синяя) и функциональная ось (красная) сустава MP. (B) Положение функциональной оси ( x f , y f ) и анатомической оси ( x a , y a ) в системе координат стопы. (C) Угол ориентации α, образованный функциональной (или анатомической) осью по отношению к оси X в плоскости XOZ . (D) Угол ориентации β, образованный функциональной (или анатомической) осью относительно оси Y в плоскости XOY .
3D-положения FA ( x f , y f ) и AA ( x a , y a ) описаны в плоскости XOY локальной системы координат стопы (рис. 1B), в которой начало координат расположено на верхнем гребне пяточной кости (Ren et al., 2010). Трехмерные ориентации FA и AA описываются как спроецированный угол в плоскости XOZ (α) и XOY (β) локальной анатомической системы координат стопы. На основе правила правой руки положительный угол α определяется количественно, возникающим от оси X в направлении против часовой стрелки, тогда как отрицательный угол β количественно определяется, возникающий от оси Y в направлении по часовой стрелке (Рисунки 1C, D).
Анализ данных
GMAS (Generalized Motion Analysis Software), пакет на основе MATLAB для трехмерного кинематического и кинетического анализа (Ren et al., 2005, 2008b), использовался для обработки необработанных данных, включая скорость передвижения. Испытания с более чем 10 пропущенными подряд фреймами были прекращены. В GMAS также был завершен процесс заполнения пробелов. После этого данные были отфильтрованы с применением фильтра Баттерворта четвертого порядка с нулевой задержкой нижних частот с частотой среза 6,0 Гц. Фильтр 6 Гц использовался при постобработке для уменьшения шума и сглаживания необработанных данных. Это приобретение было определено в соответствии с максимальным количеством циклов походки, которые участники могут выполнить за одну секунду, другими словами, до максимальной скорости, деленной на длину шага.В этом исследовании скорость быстрого бега составляет менее 4,8 м / с, а длина шага составляет около 0,8–1,0 м, поэтому частота отсечки была установлена на 6 Гц. Для каждой скорости бега были рассчитаны средние значения и стандартные отклонения положения и ориентации для разных испытуемых.
Испытания с более чем 10 пропущенными подряд фреймами были прекращены. В GMAS также был завершен процесс заполнения пробелов. После этого данные были отфильтрованы с применением фильтра Баттерворта четвертого порядка с нулевой задержкой нижних частот с частотой среза 6,0 Гц. Фильтр 6 Гц использовался при постобработке для уменьшения шума и сглаживания необработанных данных. Это приобретение было определено в соответствии с максимальным количеством циклов походки, которые участники могут выполнить за одну секунду, другими словами, до максимальной скорости, деленной на длину шага.В этом исследовании скорость быстрого бега составляет менее 4,8 м / с, а длина шага составляет около 0,8–1,0 м, поэтому частота отсечки была установлена на 6 Гц. Для каждой скорости бега были рассчитаны средние значения и стандартные отклонения положения и ориентации для разных испытуемых.
Поскольку размер стопы у разных испытуемых различается, параметры положения x и y как для FA, так и для AA были нормализованы по длине стопы каждого испытуемого (определяемой как смещение от исходной точки к средней точке 1-й ступни). и головки 5-й плюсневой кости).Было исследовано влияние скорости на FA, в котором также были приняты во внимание данные из предыдущей статьи, чтобы сравнить статистические различия между каждой парой скоростей и изучить изменение тенденции от медленной ходьбы к быстрому бегу. Поскольку длина ног была разной для каждого испытуемого, скорость также была нормализована, как показано ниже, чтобы количественно оценить изменение параметра положения FA в передне-заднем направлении,
и головки 5-й плюсневой кости).Было исследовано влияние скорости на FA, в котором также были приняты во внимание данные из предыдущей статьи, чтобы сравнить статистические различия между каждой парой скоростей и изучить изменение тенденции от медленной ходьбы к быстрому бегу. Поскольку длина ног была разной для каждого испытуемого, скорость также была нормализована, как показано ниже, чтобы количественно оценить изменение параметра положения FA в передне-заднем направлении,
V = νgL (1)
, где v — скорость одного цикла походки, равная dx / T ( dx — это смещение исходной точки от одного удара пяткой к следующему удару пяткой по оси X , и T определяется как количество кадров между двумя ударами пятки, деленное на частоту дискретизации 150 Гц), g — гравитационная постоянная со значением 9.816 м / с 2 и L — длина ноги каждого испытуемого от центра тазобедренного сустава до земли.
Статистический анализ Статистический анализ был проведен для оценки разницы между трехмерным положением и ориентацией функциональной оси и анатомической оси MP сустава во время бега, а также влияния скорости на FA при переходе от медленной ходьбы к быстрому бегу с использованием SPSS 20. 0 программное обеспечение (IBM, Армонк, Нью-Йорк, США). Для каждого условия были рассчитаны средние значения и стандартные ошибки положения и ориентации для разных субъектов, со стандартной ошибкой, указывающей на межсубъектную изменчивость.Как и в предыдущем исследовании (Raychoudhury et al., 2014), все параметры положения и ориентации ( x, y, и α, β) были проанализированы отдельно с использованием дисперсионного анализа (ANOVA) (случайные эффекты: субъекты и испытания; фиксированные эффекты: типы осей и шесть скоростей). Мы использовали множественное сравнение методом наименьшей значимой разницы (LSD) Фишера, чтобы исследовать разницу между двумя осями и между каждой парой скоростей. Эти сравнения были получены с помощью метода наименьших квадратов средних с учетом вероятности p <0.05 как статистически значимый.
0 программное обеспечение (IBM, Армонк, Нью-Йорк, США). Для каждого условия были рассчитаны средние значения и стандартные ошибки положения и ориентации для разных субъектов, со стандартной ошибкой, указывающей на межсубъектную изменчивость.Как и в предыдущем исследовании (Raychoudhury et al., 2014), все параметры положения и ориентации ( x, y, и α, β) были проанализированы отдельно с использованием дисперсионного анализа (ANOVA) (случайные эффекты: субъекты и испытания; фиксированные эффекты: типы осей и шесть скоростей). Мы использовали множественное сравнение методом наименьшей значимой разницы (LSD) Фишера, чтобы исследовать разницу между двумя осями и между каждой парой скоростей. Эти сравнения были получены с помощью метода наименьших квадратов средних с учетом вероятности p <0.05 как статистически значимый.
Результаты
На рис. 2 показаны данные о положении AA (синим цветом) и FA (красным цветом) сустава MP для всех шести испытуемых при всех трех различных скоростях бега (медленной, нормальной и быстрой). В целом было обнаружено, что АА последовательно располагается позади ФА для всех испытуемых и для всех скоростей бега, при средней разнице в положении 32,58 мм. Результат показывает, что положение FA по оси Y смещается вниз с увеличением скорости движения.Между тем, в передне-заднем направлении (по оси X ) FA во время нормального и быстрого бега не показывает никаких изменений, но при низкой скорости бега он представляет очень небольшое движение назад, но остается впереди AA. По сравнению с FA, AA не показывает отчетливого изменения положения по всем направлениям с увеличением скорости для всех испытуемых.
В целом было обнаружено, что АА последовательно располагается позади ФА для всех испытуемых и для всех скоростей бега, при средней разнице в положении 32,58 мм. Результат показывает, что положение FA по оси Y смещается вниз с увеличением скорости движения.Между тем, в передне-заднем направлении (по оси X ) FA во время нормального и быстрого бега не показывает никаких изменений, но при низкой скорости бега он представляет очень небольшое движение назад, но остается впереди AA. По сравнению с FA, AA не показывает отчетливого изменения положения по всем направлениям с увеличением скорости для всех испытуемых.
Рис. 2. Положения анатомической оси (синий) и функциональной оси (красный) сустава MP для всех шести испытуемых (A – F) на всех трех скоростях бега (медленный, нормальный, быстрый) .Сплошные точки обозначают среднее значение; полоски обозначают зоны 1 SD.
Параметры ориентации, угол α и β как FA (красный), так и AA (синий) на всех скоростях движения (медленной, нормальной и быстрой), были представлены на рисунках 3, 4. Как правило, в поперечной плоскости Ориентация FA сустава MP была более наклонной (больший угол α) к оси Z , чем ориентация AA для всех субъектов, кроме субъекта B во время медленного и нормального бега (рис. 3). Но явного изменения наклона обеих осей (FA и AA) с увеличением скорости движения не наблюдалось.Из рисунка 4 следует, что у всех испытуемых ФА показала совершенно иную ориентацию, чем АА, в сагиттальной плоскости на всех скоростях бега. Функциональная ось имела больший угол β, чем анатомическая ось, что приводило к более наклонной ориентации к оси Y , и этот наклон увеличивался от медленного к быстрому бегу. С другой стороны, угол ориентации β в сагиттальной плоскости для AA оставался небольшим различием при изменении скорости.
Как правило, в поперечной плоскости Ориентация FA сустава MP была более наклонной (больший угол α) к оси Z , чем ориентация AA для всех субъектов, кроме субъекта B во время медленного и нормального бега (рис. 3). Но явного изменения наклона обеих осей (FA и AA) с увеличением скорости движения не наблюдалось.Из рисунка 4 следует, что у всех испытуемых ФА показала совершенно иную ориентацию, чем АА, в сагиттальной плоскости на всех скоростях бега. Функциональная ось имела больший угол β, чем анатомическая ось, что приводило к более наклонной ориентации к оси Y , и этот наклон увеличивался от медленного к быстрому бегу. С другой стороны, угол ориентации β в сагиттальной плоскости для AA оставался небольшим различием при изменении скорости.
Рисунок 3. Угол ориентации α, образованный анатомической осью (синяя) и функциональной осью (красный) для всех шести испытуемых (A – F) на всех трех скоростях бега (медленный, нормальный, быстрый). Сплошные линии обозначают среднее значение; пунктирными линиями обозначены зоны 1 SD.
Рис. 4. Угол ориентации β, образованный анатомической осью (синяя) и функциональной осью (красный) для всех шести испытуемых (A – F) и для всех трех скоростей бега (медленный, нормальный, быстрый). Сплошные линии обозначают среднее значение; пунктирными линиями обозначены зоны 1 SD.
Результаты статистического анализа трехмерной ориентации и различий положения между FA и AA были описаны в таблице 1. Мы обнаружили, что, за исключением параметра положения y при медленном движении, статистически значимые различия существовали по всем параметрам ( x, y , α, β) на всех трех скоростях движения. При нормальном и быстром беге ФА расположена кпереди и ниже, чем АА, что значимо в обоих направлениях (вертикальном и горизонтальном).Кроме того, разница в углах ориентации была менее значительной в поперечной плоскости, чем в сагиттальной плоскости.
Таблица 1. Статистический анализ трехмерной ориентации и различий положения между FA и AA шарнира MP во время спуска.
Как показано в таблице 2, другой статистический анализ был проведен для изучения влияния скорости на трехмерное положение и ориентацию FA. В этом исследовании данные бега сравнивались с данными ходьбы (Raychoudhury et al., 2014), и были обнаружены некоторые существенные различия при переходе от ходьбы к бегу. Здесь было проведено попарное сравнение каждой отдельной скорости. Результаты показывают, что положение FA на оси X показало статистически значимую разницу при увеличении скорости от ходьбы к бегу. Более того, при увеличении скорости от медленной ходьбы к медленному бегу также наблюдалось прямое смещение FA в переднем направлении. Но при дальнейшем увеличении скорости до нормального и быстрого бега было обнаружено, что положение FA в передне-заднем направлении немного сдвинулось назад.Никаких значительных изменений не наблюдалось при увеличении скорости до бега, за исключением обычного бега, который показал статистически значимую разницу между медленным и нормальным бегом.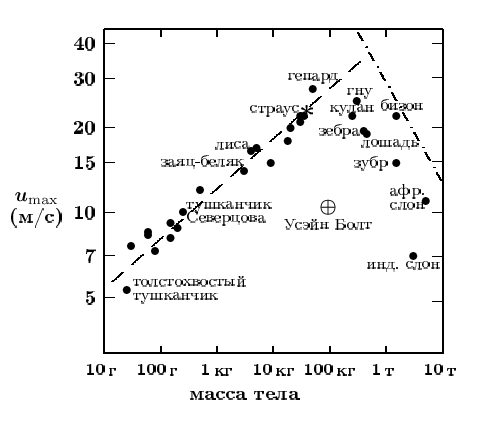
Таблица 2. Статистический анализ влияния увеличения скорости от ходьбы к бегу на положение и ориентацию функциональной оси (FA) сустава MP.
Более значительные изменения наблюдались в направлении Y , когда скорость постепенно увеличивалась от медленной ходьбы к быстрой.В нашем предыдущем исследовании (Raychoudhury et al., 2014) FA начинала двигаться к более высокому положению, когда скорость увеличивалась с медленной ходьбы на быструю. Интересно, что когда скорость была увеличена до медленного бега с последующим нормальным бегом и быстрым бегом, наблюдалось движение FA к более низкому положению. Существенные различия были обнаружены в обычном и быстром пробегах, где FA двигалась даже ниже исходной. Мы не обнаружили статистически значимых эффектов на угол α FA в поперечной плоскости при увеличении скорости от ходьбы к бегу, за исключением медленной ходьбы и обычного бега.Однако более значимые эффекты были обнаружены в угле ориентации ФА β в сагиттальной плоскости. Ориентация FA сильно изменилась во время быстрой скорости бега, что показало статистически значимое отличие от остальных пяти скоростей. При переходе от медленной ходьбы к медленному бегу в этой ориентации не было обнаружено значительных эффектов. А нормальный бег показал статистически значимую разницу между первыми двумя скоростями ходьбы и быстрого бега. Обычно при постепенном увеличении скорости ФА становилась более наклонной в сагиттальной плоскости.
Ориентация FA сильно изменилась во время быстрой скорости бега, что показало статистически значимое отличие от остальных пяти скоростей. При переходе от медленной ходьбы к медленному бегу в этой ориентации не было обнаружено значительных эффектов. А нормальный бег показал статистически значимую разницу между первыми двумя скоростями ходьбы и быстрого бега. Обычно при постепенном увеличении скорости ФА становилась более наклонной в сагиттальной плоскости.
На рисунке 5 показан тренд параметра положения x и y , нормализованный по длине стопы, с нормализованной скоростью V . Можно видеть, что положение x FA шарнира MP смещается вперед до медленного хода, а затем для нормального хода и быстрого хода ось смещается назад без разницы между двумя последними рабочими скоростями. Параметр нормализованного положения y перемещался вверх в верхнем направлении во время медленного, нормального и быстрого ходьбы.Но при дальнейшем увеличении скорости положение FA y сместилось больше в нижнем направлении. Кроме того, он смещался ниже начала координат при обычном и быстром беге.
Кроме того, он смещался ниже начала координат при обычном и быстром беге.
Рис. 5. Тенденция положения x и y (нормализованная по длине стопы) FA с нормализованной скоростью V , возрастающей от медленной ходьбы к быстрому бегу. Круглые графики обозначают среднее значение; полоски обозначают зоны 1 SD.
На рисунке 6 изображена тенденция угла ориентации α и β FA сустава MP в сагиттальной плоскости с увеличением нормированной скорости V от медленной ходьбы к быстрому бегу.В поперечной плоскости явного тренда угла α не обнаружено. Однако, в отличие от угла α, угол ориентации β показал очевидную тенденцию с увеличением скорости. А именно, по мере увеличения нормализованной скорости ориентация FA в сагиттальной плоскости становилась более наклонной к оси Y .
Рис. 6. Тенденция увеличения угла ориентации α и β FA с нормализованной скоростью V от медленного шага к быстрому бегу. Круглые графики обозначают среднее значение; полоски обозначают зоны 1 SD.
Круглые графики обозначают среднее значение; полоски обозначают зоны 1 SD.
Обсуждение
Целью исследования является расширение исследования трехмерного положения и ориентации МП-сустава человека от ходьбы до бега. Подобно ходьбе, трехмерная ориентация и положение FA во время бега близки к AA, и наблюдались статистически значимые различия между функциональной осью и анатомической осью. FA оставался впереди AA для всех условий скорости бега со средней дистанцией около 19% FL. По сравнению с ходьбой переднезаднее положение FA смещено вперед на 3% во время бега.В вертикальном направлении FA переместился примерно на 4,8% FL в сторону более низкого положения, чем AA во время нормального и быстрого бега. В отличие от данных ходьбы, FA во время бега перемещается вниз, даже ниже начала локальной системы координат стопы. Кроме того, FA показывает более высокий наклон, чем AA на всех скоростях бега с передней нижней ориентацией. Это указывает на то, что представление соединения MP с AA может привести к неправильной оценке момента / мощности сустава и неточному расчету плеча момента, особенно для бега.
Было обнаружено статистически значимое влияние на положение и ориентацию FA, когда скорость постепенно увеличивалась от ходьбы к бегу. Подобно ходьбе, когда скорость увеличивалась до бега, FA сдвигалась в сторону более переднего положения. С другой стороны, с увеличением скорости бега FA сместилась в нижнее положение (верхнее при ходьбе). Другими словами, эта ось сустава MP показывала движение вперед по направлению к вектору силы реакции опоры во время фазы поздней стойки, когда скорость увеличивалась от ходьбы к бегу.Также было замечено, что ориентация FA становилась более наклонной по мере увеличения скорости движения. В результате моментное плечо GRF уменьшалось с одновременным увеличением моментного плеча мышц-разгибателей MP, и эта обратная зависимость будет увеличиваться с увеличением скорости. Соответственно, увеличение эффективного механического преимущества (EMA) соответствующих мышц (Biewener, 1989, 1990, 2003; Biewener et al., 2004) может достигать максимума во время быстрого бега. Таким же образом увеличенное расстояние рычага до голеностопного сустава, полученное благодаря смещению вперед FA, будет увеличиваться с увеличением скорости от ходьбы к бегу.Все это может обеспечить сокращение мышц-разгибателей MP в оптимальной области мощности с надлежащей скоростью (Biewener, 2003). Кроме того, результаты показывают, что MP-сустав также функционирует как переменная передача, особенно во время бега (Carrier et al., 1994), что улучшит локомоторные характеристики, поддерживая работу мышц-разгибателей MP в области высокой эффективности силы — кривая скорости.
Таким же образом увеличенное расстояние рычага до голеностопного сустава, полученное благодаря смещению вперед FA, будет увеличиваться с увеличением скорости от ходьбы к бегу.Все это может обеспечить сокращение мышц-разгибателей MP в оптимальной области мощности с надлежащей скоростью (Biewener, 2003). Кроме того, результаты показывают, что MP-сустав также функционирует как переменная передача, особенно во время бега (Carrier et al., 1994), что улучшит локомоторные характеристики, поддерживая работу мышц-разгибателей MP в области высокой эффективности силы — кривая скорости.
У этого исследования были некоторые ограничения. Прежде всего, движение между задним и передним отделом стопы на протяжении фазы стойки было представлено одним шарниром.Вариант с одной осью для MP-сустава забыл, что первый палец ноги имеет решающее значение в двигательной фазе движения человека и в большинстве случаев имеет другую ориентацию оси по сравнению с другими четырьмя пальцами. В будущих исследованиях этому следует уделить больше внимания. Во-вторых, фаланги и сегменты заднего отдела стопы рассматривались как отдельные жесткие сегменты. Однако между фалангами или костями заднего отдела стопы могут наблюдаться относительные движения. В-третьих, в этом исследовании приняли участие только 6 взрослых, и мы привлечем больше участников и проведем анализ мощности для дальнейших исследований.Кроме того, могут присутствовать некоторые кожные артефакты из-за маркеров кожи, участвующих в измерении походки. В будущем для количественной оценки совместных движений будет использоваться бипланная рентгеновская система визуализации.
Во-вторых, фаланги и сегменты заднего отдела стопы рассматривались как отдельные жесткие сегменты. Однако между фалангами или костями заднего отдела стопы могут наблюдаться относительные движения. В-третьих, в этом исследовании приняли участие только 6 взрослых, и мы привлечем больше участников и проведем анализ мощности для дальнейших исследований.Кроме того, могут присутствовать некоторые кожные артефакты из-за маркеров кожи, участвующих в измерении походки. В будущем для количественной оценки совместных движений будет использоваться бипланная рентгеновская система визуализации.
Заключение
y В этом исследовании мы статистически оценили разницу между функциональной осью MP-сустава человека и анатомической осью, обычно используемой в литературе, во время бега с разными скоростями. Была представлена трехмерная наклонная ориентация функциональной оси вместе с ее относительным положением в системе координат стопы.Положение FA находится впереди и выше AA в более наклонной ориентации во время бега, как при ходьбе. Статистический анализ был проведен для изучения влияния скорости локомоторного движения в диапазоне от медленной ходьбы до быстрого бега на положение и ориентацию суставов MP путем интеграции с набором данных о ходьбе, полученным в нашем предыдущем исследовании. С увеличением скорости передвижения ось сустава смещается вперед в передне-заднем направлении, но в верхнем-нижнем направлении она сначала движется вверх, а затем смещается вниз.Увеличение моментного плеча мышц-разгибателей MP и уменьшение моментного плеча GRF может помочь смягчить мышечное усилие мышц-разгибателей MP, увеличить EMA мышцы и улучшить двигательные функции. Эти находки позволят лучше понять основной механизм биомеханической функции плюснефалангового сустава in vivo во время движения. Более того, они могут улучшить бионические конструкции ног роботов, терапевтической обуви и даже протезов нижних конечностей.
Статистический анализ был проведен для изучения влияния скорости локомоторного движения в диапазоне от медленной ходьбы до быстрого бега на положение и ориентацию суставов MP путем интеграции с набором данных о ходьбе, полученным в нашем предыдущем исследовании. С увеличением скорости передвижения ось сустава смещается вперед в передне-заднем направлении, но в верхнем-нижнем направлении она сначала движется вверх, а затем смещается вниз.Увеличение моментного плеча мышц-разгибателей MP и уменьшение моментного плеча GRF может помочь смягчить мышечное усилие мышц-разгибателей MP, увеличить EMA мышцы и улучшить двигательные функции. Эти находки позволят лучше понять основной механизм биомеханической функции плюснефалангового сустава in vivo во время движения. Более того, они могут улучшить бионические конструкции ног роботов, терапевтической обуви и даже протезов нижних конечностей.
Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без излишних оговорок.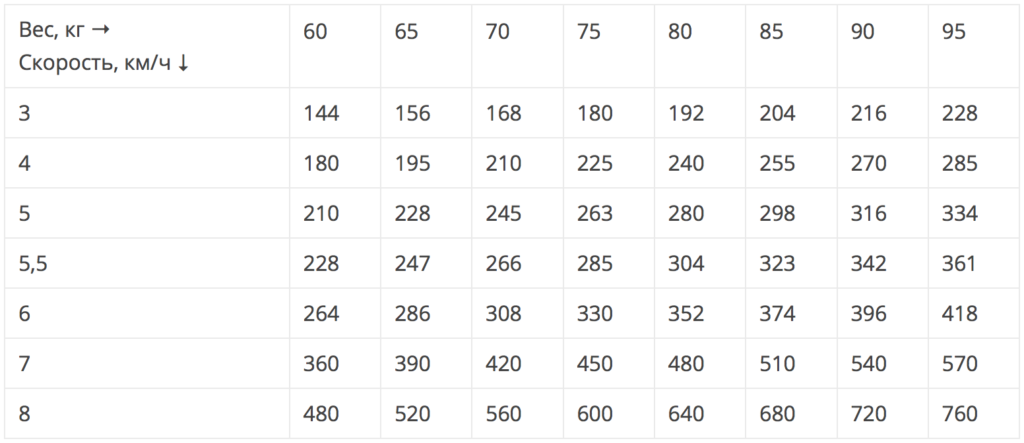
Заявление об этике
Исследования с участием людей были рассмотрены и одобрены Консультативным комитетом по этике университета. Пациенты / участники предоставили письменное информированное согласие на участие в этом исследовании.
Взносы авторов
LR, ZQ и GW разработали это исследование.KW, SR и LR провели эксперименты и составили рукопись. DH, JL, HX, WL и BL отвечали за обработку данных, обсуждения и исправления. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Это исследование было частично поддержано проектом Национальной программы ключевых исследований и разработок Китая (№ 2018YFC2001300), проектом Национального фонда естественных наук Китая (№ 91948302, № 91848204, № 52005209 и № 51675222). и Китайская программа международного обмена постдокторантами.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы благодарим Джона Р. Хатчинсона за его помощь в измерении походки и сборе данных.
Список литературы
Альтман, А. Р., Дэвис, И. С. (2012). Кинематический метод определения рисунка ударов у бегунов босиком и в обуви. Поза походки 35, 298–300. DOI: 10.1016 / j.gaitpost.2011.09.104
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Апкариан Дж., Науманн С. и Кэрнс Б. (1989). Трехмерная кинематическая и динамическая модель нижней конечности. J. Biomech. 22, 143–155. DOI: 10.1016 / 0021-9290 (89) -7
CrossRef Полный текст | Google Scholar
Бивенер А. А. (2003). Передвижение животных. Нью-Йорк, Нью-Йорк: Oxford University Press Inc.
Google Scholar
Бивенер А. А., Фарли К. Т., Робертс Т. Дж. И Теманер М. (2004). Мышечные механические преимущества ходьбы и бега человека: влияние на стоимость энергии. J. Appl. Physiol. 97, 2266–2274. DOI: 10.1152 / japplphysiol.00003.2004
DOI: 10.1152 / japplphysiol.00003.2004
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Каппоццо А., Катани Ф., Делла Кроче У. и Лирдини А. (1995). Положение и ориентация в пространстве костей при движении: определение и определение анатомической структуры. Clin. Биомех. 10, 171–178. DOI: 10.1016 / 0268-0033 (95) 91394-T
CrossRef Полный текст | Google Scholar
Карсон, М. К., Харрингтон, М. Э., Томпсон, Н., О’Коннор, Дж. Дж., И Теологис, Т. Н. (2001). Кинематический анализ многосегментной модели стопы для исследований и клинических применений: анализ повторяемости. J. Biomech. 34, 1299–1307. DOI: 10.1016 / S0021-9290 (01) 00101-4
CrossRef Полный текст | Google Scholar
Кавана, П.Р. и Лафортюн М.А. (1980). Силы реакции опоры при беге на длинные дистанции. J. Biomech. 13, 397–406. DOI: 10.1016 / 0021-9290 (80) -0
CrossRef Полный текст | Google Scholar
Czerniecki, J. M. (1988). Биомеханика стопы и голеностопного сустава при ходьбе и беге. Обзор. Am. J. Phys. Med. Rehabil. 67, 246–252.
M. (1988). Биомеханика стопы и голеностопного сустава при ходьбе и беге. Обзор. Am. J. Phys. Med. Rehabil. 67, 246–252.
Google Scholar
Гамейдж, С. С. Х. У., Ласенби, Дж. (2002). Новые решения методом наименьших квадратов для оценки среднего центра вращения и оси вращения. J. Biomech. 35, 87–93. DOI: 10.1016 / S0021-9290 (01) 00160-9
CrossRef Полный текст | Google Scholar
Гефен А., Мегидо-Равид М., Ицчак Ю. и Аркан М. (2000). Биомеханический анализ трехмерной структуры стопы во время ходьбы: основной инструмент для клинического применения. J. Biomech. Англ. 122, 630–639. DOI: 10.1115 / 1.1318904
CrossRef Полный текст | Google Scholar
Кер, Р. Ф., Беннет, М. Б., Бибби, С. Р., Кестер, Р.К. и Александр Р. М. (1987). Пружина в своде стопы человека. Природа 325, 147–149. DOI: 10.1038 / 325147a0
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ким Ю., Ким С., Сон Дж. И Чон Б. (2012). Кинетическая роль плюснефалангового сустава при нормальной ходьбе: суставной момент и сила. Внутр. J. Precis. Англ. Manuf. 13, 1481–1485. DOI: 10.1007 / s12541-012-0195-z
И Чон Б. (2012). Кинетическая роль плюснефалангового сустава при нормальной ходьбе: суставной момент и сила. Внутр. J. Precis. Англ. Manuf. 13, 1481–1485. DOI: 10.1007 / s12541-012-0195-z
CrossRef Полный текст | Google Scholar
Липферт, С.В., Гюнтер, М., Реневски, Д., Гриммер, С., и Зейфарт, А. (2012). Сравнение модели-эксперимента системной динамики для ходьбы и бега человека. J. Theor. Биол. 292, 11–17. DOI: 10.1016 / j.jtbi.2011.09.021
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Манн Р. А. и Хэги Дж. Л. (1979). Функция пальцев ног при ходьбе, беге трусцой и беге. Clin. Ортоп. Relat. Res. 142, 24–29. DOI: 10.1097 / 00003086-197
0-00005
CrossRef Полный текст | Google Scholar
Минетти, А.Э., Ардиго, Л. П., и Сайбене, Ф. (1994). Переход между ходьбой и бегом у людей: метаболические и механические аспекты на разных уровнях. Acta Physiol. Сканд. 150, 315–323. DOI: 10.1111 / j. 1748-1716.1994.tb09692.x
1748-1716.1994.tb09692.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Нестер, К. Дж., Лю, А. М., Уорд, Э., Ховард, Д., Кочеба, Дж., Деррик, Т. и др. (2007). Исследование кинематики стопы in vitro на динамической модели трупа при ходьбе. J. Biomech. 40, 1927–1937. DOI: 10.1016 / j.jbiomech.2006.09.008
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Нильссон, Дж., И Торстенссон, А. (1987). Адаптивность по частоте и амплитуде движений ног при движении человека с разной скоростью. Acta Physiol. Сканд. 129, 107–114. DOI: 10.1111 / j.1748-1716.1987.tb08045.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Нильссон, Дж., И Торстенссон, А. (1989).Силы реакции земли при разных скоростях ходьбы и бега человека. Acta Physiol. Сканд. 136, 217–227. DOI: 10.1111 / j.1748-1716.1989.tb08655.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Райчоудхури, С. , Ху, Д., и Рен, Л. (2014). Трехмерная кинематика плюснефалангового сустава человека при ходьбе по прямой. Фронт. Bioeng. Biotechnol. 2:73. DOI: 10.3389 / fbioe.2014.00073
, Ху, Д., и Рен, Л. (2014). Трехмерная кинематика плюснефалангового сустава человека при ходьбе по прямой. Фронт. Bioeng. Biotechnol. 2:73. DOI: 10.3389 / fbioe.2014.00073
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Рен, Л., Ховард, Д., Рен, Л., Нестер, К., и Тиан, Л. (2008a). Фазозависимая гипотеза локомоторных функций комплекса стопы человека. J. Bionic Eng. 5, 175–180. DOI: 10.1016 / S1672-6529 (08) 60022-0
CrossRef Полный текст | Google Scholar
Рен, Л., Ховард, Д., Рен, Л., Нестер, К., и Тиан, Л. (2010). Общая аналитическая модель опрокидывания стопы для прогнозирования поступательной кинематики голеностопного сустава в исследованиях моделирования походки. J. Biomech. 43, 194–202. DOI: 10.1016 / j.jbiomech.2009.09.027
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Рен, Л., Джонс, Р. К., и Ховард, Д. (2008b). Обратная динамика всего тела в течение полного цикла походки, основанная только на измеренной кинематике.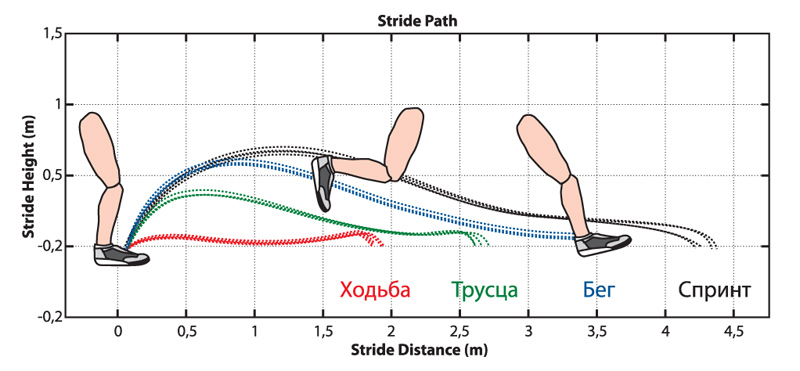 J. Biomech. 41, 2750–2759. DOI: 10.1016 / j.jbiomech.2008.06.001
J. Biomech. 41, 2750–2759. DOI: 10.1016 / j.jbiomech.2008.06.001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Скотт, С. Х., Уинтер, Д. А. (1993). Биомеханическая модель стопы человека: кинематика и кинетика во время фазы опоры при ходьбе. J. Biomech. 26, 1091–1104. DOI: 10.1016 / S0021-9290 (05) 80008-9
CrossRef Полный текст | Google Scholar
Смит, Г., Лейк, М., Лис, А., Уорсфолд, П. (2012). Процедуры измерения влияют на интерпретацию функции плюснефалангового сустава во время ускоренного спринта. J. Sports Sci. 30, 1521–1527. DOI: 10.1080 / 02640414.2012.713501
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Стефанишин, Д. Дж., И Нигг, Б.М. (1997). Вклад механической энергии плюснефалангового сустава в бег и спринт. J. Biomech. 30, 1081–1085. DOI: 10.1016 / S0021-9290 (97) 00081-X
CrossRef Полный текст | Google Scholar
Стефанишин, Д. Дж., И Нигг, Б. М. (1998). Вклад суставов нижних конечностей в механическую энергию при беге вертикальных прыжков и беге в прыжках в длину. J. Sports Sci. 16, 177–186. DOI: 10.1080 / 026404198366885
М. (1998). Вклад суставов нижних конечностей в механическую энергию при беге вертикальных прыжков и беге в прыжках в длину. J. Sports Sci. 16, 177–186. DOI: 10.1080 / 026404198366885
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Vereecke, E.Э., и Аэртс, П. (2008). Механика стопы гиббона и ее потенциал для накопления упругой энергии при двуногом движении. J. Exp. Биол. 211, 3661–3670. DOI: 10.1242 / jeb.018754
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Зелик К. Э., Такахаши К. З., Савицкий Г. С. (2015). Анализ шести степеней свободы бедра, колена, голеностопного сустава и стопы обеспечивает обновленное понимание биомеханической работы во время ходьбы человека. J. Exp. Биол. 218, 876–886.DOI: 10.1242 / jeb.115451
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Как быстро люди могут идти?
Люди довольно шустры. В 2009 году Усэйн Болт пролетел по трассе со скоростью более 23 миль в час; В 2014 году Деннис Киметто, рекордсмен мира по марафону, проехал 26,2 мили со скоростью 12,8 миль в час (примерно 4:42 на милю). Ученые выясняют, что движет стрелами и кимето в мире, и как мы эволюционировали, чтобы делать и то, и другое. Эти знания переопределяют возможности и могут помочь вам ускориться.
Ученые выясняют, что движет стрелами и кимето в мире, и как мы эволюционировали, чтобы делать и то, и другое. Эти знания переопределяют возможности и могут помочь вам ускориться.
Типы мышечных волокон
Мышечные волокна бывают двух основных типов: быстрые и медленно сокращающиеся, и у всех есть сочетание обоих. Быстро сокращающиеся волокна предназначены для коротких мощных импульсов; они быстро сокращаются, но также быстро утомляются. Медленно сокращающиеся волокна содержат больше митохондрий — электростанций клеток, которые используют кислород для производства энергии, поэтому они не так легко утомляются и идеально подходят для более длительной активности.
Как вы могли догадаться, у спринтеров больше быстрых волокон, а у спортсменов на выносливость — медленнее.Хотя это частично генетически, есть некоторые свидетельства того, что мы можем тренироваться, чтобы изменить пропорцию волокон в наших мышцах. Например, бег на длинные дистанции в медленном темпе может увеличить процент медленно сокращающихся волокон человека.
Поперечные сечения мышц ног Слева: больше волокон FAST-TWITCH (легких): лучше для бега на короткие дистанции. Справа: больше МЕДЛЕННЫХ волокон (темные): лучше для выносливости. Элисон Макки / Откройте для себя
Анатомия бегуна
Факторы быстроты: спринт Всем требуется одинаковое количество времени между шагами и одинаковое количество времени, чтобы поднять ногу и снова положить ее, но более быстрые спринтеры продвигаются дальше за это время.«Разница в скорости действительно зависит от того, что происходит на земле», — говорит Питер Вейанд, физиолог и биомеханик из Южного методистского университета в Техасе. «Быстрые люди бьют с большей силой по сравнению с массой тела».
Элитные спринтеры используют свои ноги, чтобы «по сути нанести удар по земле», — объясняет он. Они получают эту дополнительную силу от своего характерного подъема колен: поднятие колена выше дает ноге больше места для набора скорости, прежде чем она ударится о землю, поэтому она ударяется с большей силой.
Чтобы бежать быстрее, Вейанд предлагает две вещи. Во-первых, постарайтесь быстрее оторвать ногу от земли. Когда передняя нога приземляется, колено задней ноги должно быть на одном уровне с коленом приземления; если он все еще находится за приземляющимся коленом, подъем колена перед телом может быть затруднен, что ослабит удар. Во-вторых, при приземлении постарайтесь сохранять неподвижность. Элитные спринтеры не позволяют чему-либо рушиться — ни гибким лодыжкам, ни кривым коленям, ни даже движениям головы — поэтому они не теряют силу, когда снова отрываются от земли.
Факторы быстроты: бег на расстояние
Для быстрого бега на длинные дистанции ключевым моментом является энергоснабжение. Если вы бежите быстрее, чем ваше тело может поставлять энергию, вам придется замедлиться. «Так что игра для бегунов на длинные дистанции действительно экономит», — говорит Вейанд. «Чем быстрее вы бежите при меньшем расходе энергии, тем лучше вам».
Есть два способа улучшить энергоснабжение при сохранении быстрого зажима: либо производить больше энергии, либо сжигать меньше. Производство большего количества означает увеличение так называемого VO2max, максимального количества кислорода, которое вы можете получить и превратить в энергию во время тренировки.Высокий уровень VO2max отчасти обусловлен генетикой, но отчасти его можно тренировать, особенно для начинающих бегунов. Чтобы усилить его, выполняйте интервальные тренировки: после разминки интенсивно бегайте в течение 3-5 минут, затем бегайте трусцой в течение 2-3 минут для восстановления. Повторите примерно пять раз перед бегом на заминку.
Производство большего количества означает увеличение так называемого VO2max, максимального количества кислорода, которое вы можете получить и превратить в энергию во время тренировки.Высокий уровень VO2max отчасти обусловлен генетикой, но отчасти его можно тренировать, особенно для начинающих бегунов. Чтобы усилить его, выполняйте интервальные тренировки: после разминки интенсивно бегайте в течение 3-5 минут, затем бегайте трусцой в течение 2-3 минут для восстановления. Повторите примерно пять раз перед бегом на заминку.
Чтобы сжигать меньше энергии, вам необходимо повысить эффективность или экономичность. Способы сделать это менее конкретизированы, чем методы увеличения вашего VO2max, но Вейанд говорит, что может помочь типичный подход к постепенному сглаживанию перед большим мероприятием — сокращение пробега и выполнение более быстрых тренировок.Но Алекс Хатчинсон, автор книги «Выносить: разум, тело и удивительно эластичные пределы человеческой деятельности», говорит, что лучше всего просто больше бегать. Однако он признает, что большинству бегунов-любителей не хватает времени и они склонны к травмам. В этом случае могут помочь уроки, извлеченные из двухчасовых попыток марафона (см. «Точка разрыва» справа): оптимизация питания, стратегия гонки и, возможно, даже модная обувь могут помочь нам сделать все, что в наших силах, с тем, что у нас есть.
Однако он признает, что большинству бегунов-любителей не хватает времени и они склонны к травмам. В этом случае могут помочь уроки, извлеченные из двухчасовых попыток марафона (см. «Точка разрыва» справа): оптимизация питания, стратегия гонки и, возможно, даже модная обувь могут помочь нам сделать все, что в наших силах, с тем, что у нас есть.
На доисторической пещерной картине в Ливии изображен охотник, преследующий добычу.Пьер Марко Такка / Getty Images
Адаптация к выносливости
Согласно теории, ставшей известной Деннисом Брамблом и Дэниелом Либерманом в статье Nature 2004 года, люди рождены, чтобы бегать — и бегать далеко.
«Существует множество [приспособлений], которые не имеют ничего общего с ходьбой», — говорит Либерман, биолог-эволюционист из Гарвардского университета. «Это всего лишь приспособления для бега по умопомрачению». Теория предполагает, что ранние люди развили эти приспособления, наряду с отслеживанием, чтобы преследовать антилоп, пока животные не упали от истощения и теплового удара. Победа в беге означала обед.
Победа в беге означала обед.
Сохранение спокойствия: Помимо того, что у нас нет шерсти, у нас гораздо больше потовых желез, чем у большинства других млекопитающих, что дает нам преимущество перед более пушистыми животными, которым приходится останавливаться и тяжело дышать, чтобы остыть.
Ребенок вернулся: большая ягодичная мышца — большая задница — отличительная черта человека. Мы минимально полагаемся на него при ходьбе, но он очень важен для стабилизации во время бега.
Пружинные сухожилия. У наших ног длинные сухожилия, такие как ахиллесовы, которые действуют как пружины, помогая генерировать силу и снижая затраты энергии при беге.И похоже, что они не приносят особой пользы ходьбе — еще одно свидетельство того, что наши тела созданы для бега.
Breaking Point
Олимпиец Элиуд Кипчоге в кроссовках Nike Zoom Vaporfly Elite, призванных помочь ему и другим элитным бегунам преодолеть двухчасовой барьер марафона. Роберт Дж. Престон / Алами Стоковое Фото
В декабре 2016 года, установив мировой рекорд марафона в 2:02:57, Nike объявила дерзкую цель: преодолеть двухчасовой барьер.
Эксперты поначалу возмутились.Но в мае прошлого года Элиуд Кипчоге, олимпийский чемпион-марафонец 2016 года из Кении, пробежал 2:00:25 — всего на одну секунду на милю ниже необходимого темпа.
Спортивное руководство не считает пробег Кипчоге мировым рекордом, потому что он не соблюдает правила для официальных рекордов. Но физиологи используют его, чтобы изобретать способы преодолеть порог на рекордно приемлемом курсе.
Хатчинсон полагает, что Кипчоге помогло несколько факторов. Новая технология обуви Nike, разработанная для этого проекта, вероятно, сэкономила минуту.Он потерял, возможно, еще одну минуту, занимаясь драфтом — уменьшая сопротивление ветру, бегая за кем-то другим, в данном случае иноходцем, — и 30 секунд на других вещах, таких как ровный курс.
На Берлинском марафоне прошлой осенью бегуны уже приняли стратегию драфта. Новая обувь Nike Zoom Vaporfly Elite вызывает споры; компания помогла профинансировать единственное опубликованное исследование о них. Но Хатчинсон считает, что доказательства достаточно убедительны, чтобы предположить, что они «не просто рекламная шумиха».
Но Хатчинсон считает, что доказательства достаточно убедительны, чтобы предположить, что они «не просто рекламная шумиха».
Weyand, также участник аналогичного проекта Sub-2, говорит, что усилия выходят за рамки обуви и черчения.Ученые также работают над оптимизацией того, сколько энергии бегуны могут извлечь из источников топлива. Чтобы преодолеть барьер, необходимо усовершенствовать комбинацию факторов.
Люди против царства животных
Хотя мировой рекорд Усэйна Болта на 100-метровой дистанции в 9,58 секунды может показаться очень быстрым, в царстве животных не так уж и много поводов для хвастовства. Гепард бежит примерно в три раза быстрее, чем Болт.
Что касается выносливости, мы складываемся немного лучше. В гонках, в которых люди сталкиваются с лошадьми, некоторые из людей — даже не элитные бегуны — побеждают некоторых из лошадей.Но Вейанд изучал вилорогих антилоп в лаборатории, специально форматируя беговые дорожки, которые могли работать достаточно быстро. Он обнаружил, что они примерно в три раза быстрее, чем лучшие марафонцы среди людей.
Он обнаружил, что они примерно в три раза быстрее, чем лучшие марафонцы среди людей.
Либерман говорит, что скребет дно бочки. На больших расстояниях «люди могут и делают… убегают от всех видов тварей», — говорит он.
Вот как мы складываемся:
Максимальные скорости Усэйн Болт: 23 миль / ч Собака: 41,6 миль / ч Лошадь: 43,5 миль / ч Гепард: 69 миль / ч
Марафон раз Упряжка на собачьих упряжках: ок. 1:13 Деннис Киметто: 2:02:57 Лошадь: около 2:10
Ограничение скорости — Как быстро человек может пробежать 100 метров?
Столетие назад, время 10.6 секунд в беге на 100 метров среди мужчин дали бы олимпийскую золотую медаль, и сама идея о том, что спринтер может пробежать 100 метров менее чем за 10 секунд, была воспринята как абсурд. Но на Олимпийских играх 1968 года американец Джим Хайнс искоренил это представление, пробежав 100 метров за 9,95 секунды. Мировой рекорд был с тех пор снижен до 9,58, отметки, установленной Усэйном Болтом из Ямайки в 2009 году.
По мере развития спортсменов и развития спортивной науки время, необходимое людям для преодоления 100 метров, сокращается, что оставляет мы размышляем над извечным вопросом: как низко он может опуститься?
Австралийский физиолог и спортивный ученый Джереми Ричмонд говорит, что есть ряд новых методов, которые спринтеры используют в попытках бегать еще быстрее.Фактически, он уверен, что рекорд на дистанции 100 метров может быть снижен ниже 9,3 секунды, возможно, к Играм в Токио 2020 года.
Одна из техник, которые цитирует Ричмонд, называется плиометрикой, также известной как тренировка прыжков.
«Сейчас мы видим, как много спортсменов, особенно с Ямайки, выполняют упражнения с барьерами, чтобы усилить сгибание бедра», — сказал Ричмонд. «Эти упражнения на сгибание бедра укрепляют камбаловидную мышцу (нижнюю часть икр), и исследования показывают сильную корреляцию между размером камбаловидной мышцы и эффективностью бега на короткие дистанции.![]()
«Сильная камбаловидная мышца может играть значительную роль в ускорении на первых 10 метрах, когда спринтер наиболее медленный».
Еще одним фактором является то, что мы могли видеть больше высоких спринтеров, таких как Болт, рост которого 6 футов 5 дюймов, после его стремительной карьеры. Ричмонд говорит, что физический рост Болта делает его идеальным прототипом спринтера.
«Исследования показывают, что если спринтер на 10 процентов выше, у него будет на 10 процентов меньше времени контакта с землей, что позволит ему бежать на 10 процентов быстрее», — сказал Ричмонд. «Однако ограничивающим фактором для более высоких спринтеров является энергия, необходимая для вывода ног вперед из-за более длинных конечностей».
Несмотря на уверенность Ричмонда в том, что мы увидим более быстрое время, ограничения существуют.
«Несомненно, [мировой рекорд] может быть еще ниже», — сказал он. «Если мы сможем заставить самых высоких спринтеров укрепить свои сгибатели бедра, а более низких спринтеров — быстрее сокращать свои мышцы, тогда мы сможем увидеть время около 9.27 секунд.
«Это, конечно, невозможно в Рио, но, возможно, в Токио. Сказав это, я сомневаюсь, что мы действительно преодолеем 9,2, потому что нагрузка, связанная с такими скоростями, вынудила бы нас иметь сверхтяжелые кости, но тогда, конечно, вес становится отрицательным фактором ».
.

 Бегать можно поодиночке или в группе, но непременно на время. Рекомендуются короткие дистанции длиной 10-20 метров. Пробегайте их по 5-6 раз подряд, затем делайте 1-2-минутный перерыв и повторяйте серию забегов. В течение одной тренировки выполняйте 3-4 сета.
Бегать можно поодиночке или в группе, но непременно на время. Рекомендуются короткие дистанции длиной 10-20 метров. Пробегайте их по 5-6 раз подряд, затем делайте 1-2-минутный перерыв и повторяйте серию забегов. В течение одной тренировки выполняйте 3-4 сета. 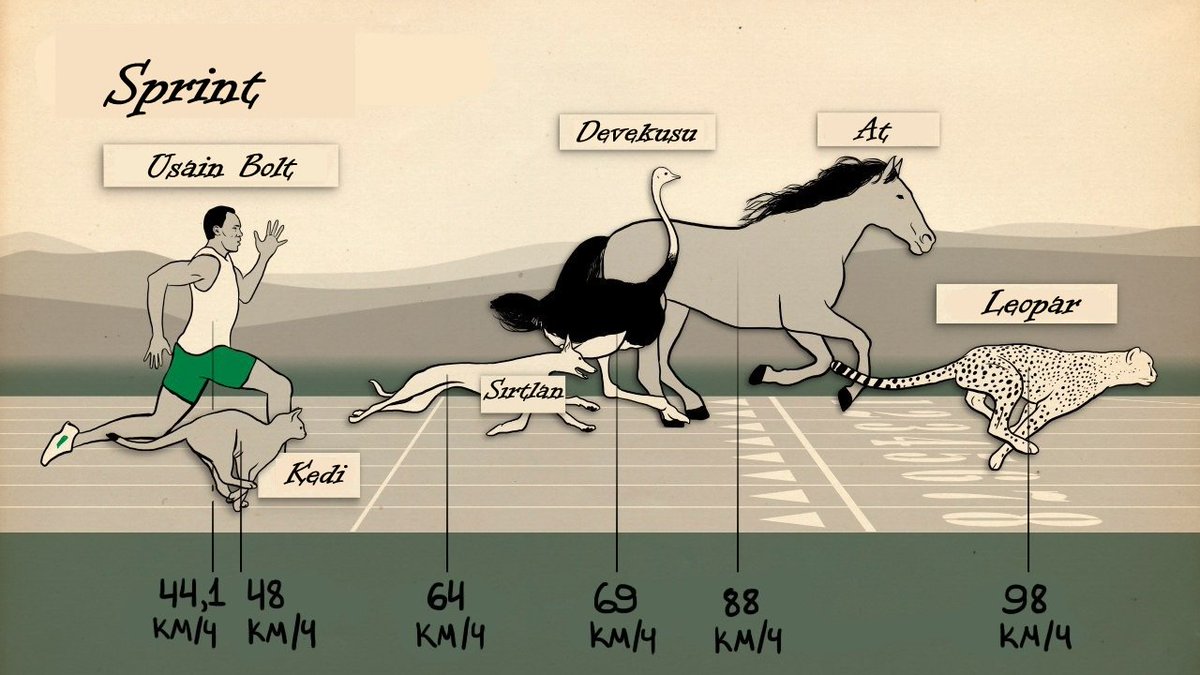 Меняя стойки, проделайте несколько сетов по 1-2 минуты каждый.
Меняя стойки, проделайте несколько сетов по 1-2 минуты каждый. Между раундами – отдых в течение 1-2 минут.
Между раундами – отдых в течение 1-2 минут.
