20 гранная кость – Нестандартные кости — Posmotre.li

Содержание

Нестандартные кости — Posmotre.li

См. также Рандом

Игральные кости 3500 год до нашей эры, и это действильно кости в самом прямом смысле этого слова^[1]

В настольных играх для определения результатов какого-либо действия традиционно применяются игральные кости. Самыми распространенными являются собственно кости — кубики, на гранях которых нанесены цифры, точки или иные символы от одного до шести. Например, в системе FATE используются специальные кости, на которых нанесены два плюса, два минуса и два пробела, а в Warhammer 40,000 есть кость разброса, на некоторые из граней которой нанесена стрелочка, указующая, в какую сторону промахнулся артиллерист.

Однако в некоторых системах настольных игр применяются нестандартные кости, имеющие число граней, отличное от шести. В большинстве случаев это так же правильные многогранники, то есть выпуклые многогранники, все грани которых являются правильными многоугольниками, а в каждой вершине сходится равное число ребер.

Традиционно кости обозначаются как dn, где n — число граней, а буква d происходит от английского слова die — собственно, игральная кость. Жаргонное название костей для настольных игр — дайсы (англ. dice — кости), или же кубики. В общем же виде результат броска костей для выполнения того или иного действия определяется по формуле mdn+k, где m — число костей, n — число граней кости, k — модификатор, который добавляется (или вычитается) к полученному в результате броска значению.

10 типов костей

d2, самая распространённая из костей. Результат её броска обычно обозначается как «орёл» или «решка». Когда нужно разыграть ворота в футболе^[2] или кто пойдёт за пивом, её и используют. А в настольных играх, когда надо разыграть «один из двух», обычно используют «чёт-нечет» или «больше-меньше».
d4, или тетраэдр — фигура в виде пирамидки из четырех треугольников. Как следует из обозначения, применяется в тех случаях, когда нужно получить число от одного до четырех. Несколько d4 можно разбросать по земле, чтобы замедлить наступление вражеской конницы.

d6, он же кубик — классический шестигранник, знакомый даже тем, кто из настольных игр видел только нарды. Самый распространенный вид дайсов. Так как они самые дешевые и их легко найти, некоторые игры не стесняются использовать их целыми ведрами. Например, Shadowrun или Warhammer 40,000 (варгейм, в НРИ по вархаммеру используется d100).
d8, октаэдр — восьмигранный кубик.
d12, додекаэдр — 12 граней. Используется редко, в основном — варварами в D&D.
d10 — т. н. пятиугольный трапецоэдр или пятиугольный дельтоэдр^[3]^[4]. Не является правильным многогранником, но используется почти так же часто, как шестигранник, потому что с его помощью легко определять результат действия в процентах (для чего надо бросить кость два раза). Поскольку это противоречит одному из законов Джеральда Камерона (не более одного броска), в стандартном наборе костей для D&D есть второй d10, размеченный в десятках.

d20, икосаэдр — двадцатигранный кубик, пользующийся особой популярностью в D&D, поскольку применяется для определения общей результативности действия. Говорим d20 — подразумеваем D&D, говорим D&D — подразумеваем d20. «Двадцать на d20» — это безусловный успех, критический удар и вообще маленькое чудо, а «единица на d20» — это катастрофическая неудача, такая, что лучше бы даже и не начинать.
d100, он же зоккиэдр — крайне редко встречающаяся кость, разработанная Лу Зокки (и названная им в свою честь), представляющая собой стогранник, плавающий внутри стеклянного шарика. Применяется в тех случаях, когда нужно получить результат от одного до ста, но большинство игроков предпочитают бросить две d10, а не гоняться за катающимся по комнате мячиком для гольфа.

В экзотических случаях встречается d3 — в таких случаях бросается d6, и если выпадает больше трёх, то из результата вычитается три — т. е., 4 = 1, 5 =2, 6 = 3. Хотя производились, где каждое значение из 1-3 было по два раза (входил в комплект игры для дошкольников «Ягодки» из набора «Три цыпленка», Изд-во «Малыш», 1982 г.). В журналах встречались версии d4 и d5 — добавлялись либо грани «переброс», либо два (одно) значения дублировались. Обычно целевой аудитории предлагалась развертка нестандартного куба для самостоятельного изготовления.

Крайне редко используют полуправильные многогранники (грань правильного делят на меньшие части). Обычно для реализации неравномерного распределения с нужными характеристиками (Formula D).

Кость d6 наиболее удобна и в изготовлении, и в броске. У бóльших костей начинает проявляться один недостаток — они слишком круглые. Чем больше граней, тем ближе кость к шару и тем легче она катится, что доставляет изрядных проблем во время игры. Меньшие, наоборот, слишком угловатые, не катаются и требуют хорошего подброса или броска из стакана.

Где встречается[править]

D&D использует все основные виды кубиков, т. е., d4, d6, d8, d10, d12 и d20. В большинстве наборов имеется и вторая кость d10, градуированная в десятках — для определения процентных результатов. Такие наборы самые популярные, в любом тематическом магазине можно найти сотни коробочек с дайсами на любой вкус и цвет, из любого материала, стоимостью от 200 рэ до бесконечности.
Ролевая система «Седьмое море» (7th Sea) — используются десятигранные кости; бросается несколько кубиков, из которых нужно выбрать указанное число кубиков; если на кости выпало 10, кость «взрывается» — перебрасывается до тех пор, пока не выпадет число, отличное от 10.
Мир тьмы: бросаются десятигранники в количестве суммы соответствующего Атрибута и Способности, учитывается количество успехов, т. е. результатов, равных или больших заданному мастером числу.

Эра Водолея: в первой части использовались шестигранники в количестве Атрибут + Навык, и результат броска — сумма всех кубиков. Во второй части остались только два кубика, один в плюс, другой в минус (тем самым результат броска имеет нормальное распределение от -5 до 5).
Dragon Age: в этой ролевой системе для любых проверок навыков используются три шестигранника, причем один из них другого цвета и называется Кубиком Дракона. При обычном броске навыка результат на Кубике Дракона определяет степень успешности (или неуспешности) действия, в то время как сама по себе успешность/неуспешность определяется суммой этих трех. Иначе говоря, если два персонажа перепрыгивали яму, оба выкинули равные результаты, но у одного на Кубике Дракона 1, а у другого 6, то первый, скорее всего, немного не долетев, уцепился за край ямы и вскарабкался на другую сторону, а другой перелетел птицей, элегантно приземлился и послал голливудскую улыбку случившимся зрителям.

↑ Простолюдины использовали в этом качестве бабки (таранная кость сустава копыта), а для фараона кости в форме бабок вырезали из слоновой кости
↑ Если быть буквоедом, в европейском футболе одна команда выбирает ворота, вторая разводит мяч. Кто есть кто, выбирается жребием. Во втором тайме команды меняются.
↑ дельтоэдр — это две соединенные основаниями пирамидки, у которых совпадают ребра оснований, тогда как трапецоэдр — похожая фигура, но одна из пирамидок повернута на полшага так, чтобы узел основания одной пирамидки пришелся на середину ребра основания другой
↑ Впрочем, нередко используется и d20 с двукратным набором значений 1-10

posmotre.li

Игральные кубики для настольных игр

Bloodborne

Catan

Citadel

Cluedo

Codenames

Conan

DC Comics

DaVICI

Deadlands

Deckscape

Descent

Dixit

Dungeons and Dragons

Elder Sign

Fallout

Five Tribes

Fluxx

Imperial settlers

Jenga

Keyforge

Kill Team

Legend of the Five Rings

Magic the Gathering

Necromunda

Pandemic

Pathfinder

Risk

Runebound

Savage Worlds

Small World

Spyfall (Находка для Шпиона)

Star Trek

Starfinder

Ticket to Ride

Twilight Imperium

Twister

War Cry

War Thunder

Warface

Warhammer

Warhammer 40000

Warhammer Age of Sigmar

Warhammer Quest

Warhammer Underworld

White Dwarf

World of Indines

World of Tanks

World of Warplanes

World of Warships

XCOM

Андор

Берсерк. Герои

Бэнг!

Властелин Колец (Lord of the Rings)

Воображарий

Время Приключений

Дисней

Древний Ужас

Замес

Звёздные Империи

Зомбицид

Игра Престолов

Каркассон

Классический Берсерк

Книги-игры

Манчкин

Мир фантастики

Монополия

Особняки Безумия

Подземелье

СЫЩИК

Свинтус

Соображарий

Таверна «Красный Дракон»

Ужас Аркхэма

Цивилизация (Sid Meier’s Civilization)

Шакал

Эволюция

Экивоки

Эпичные схватки боевых магов

hobbygames.ru

Набор игральных костей «10 в 1». Бросаем правильно

Мастер: Гном, вы оступились и провалились в расщелину среди скал. Сейчас летите вниз, скоро дно. Ваши действия?
Гном: Хммм… Ну, быстро-быстро машу руками.
Мастер: Да? Ну кидай.
Гном: 20.
Мастер: Кидай еще раз…
Гном: 20.
Мастер: Так. Дай сюда кости.(Бросает сам) Опять 20.
(со вздохом) Партия наблюдает, как из расщелины в полном боевом обмундировании быстро-быстро маша руками медленно поднимается гном…

Обычно при словах «настольная игра» представляется расчерченное поле, по которому передвигаются фишки согласно результатам бросков обычного шестигранного кубика.
На самом деле это всего лишь малая часть настольных игр с кубиками, а шестигранный куб — один из множества используемых в них кубиков. Хотя, так как не-шестигранные кубики вообще не являются кубиками по определению, то их правильнее будет называть игральными костями, или дайсами, от их английского наименования — dice.
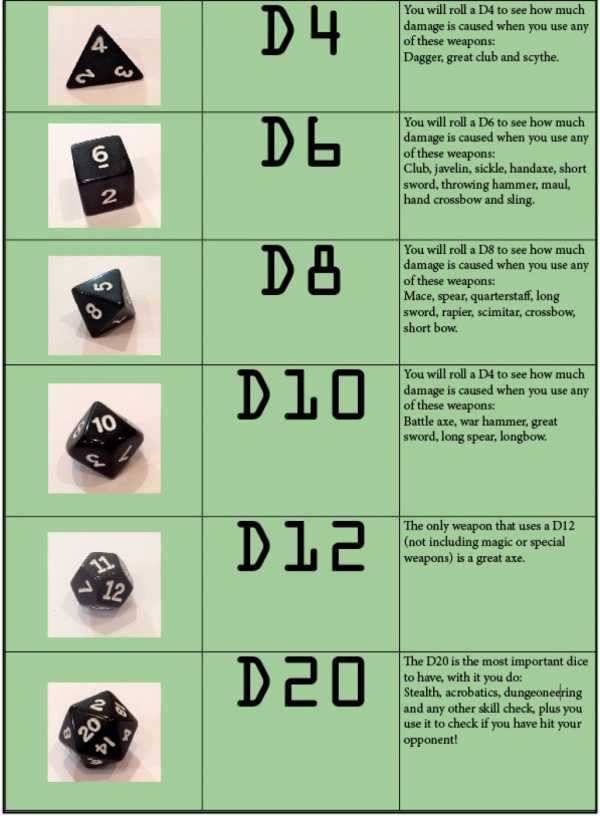
Набор из 7 костей(4-гранник, 6-гранник, 8-гранник, 2 10-гранника. 12-гранник и 20-гранник) стал считаться классическим со времён выхода игры Dungeons&Dragons в 1974 году. Кости обозначались как dN(где N — количество граней: d4, d6, d8, d10, d12, d20), а сокращение MdN обозначает сумму M применений 1dN.
Следует отметить, что MdN даёт целые числа в интервале [M..M*N]. Вероятность выпадения числа из этого интервала растёт по мере приближения к его середине.
Результатом броска 20-гранника оценивалась успешность действий персонажа, а все остальные кости использовались для определения урона от оружия:

Игра пережила с тех пор огромное количество переизданий, расширений, переизданий расширений и переписываний правил с нуля, а вот семь классических костей остались, несмотря на возможность их программной эмуляции на ПК, КПК, смартфонах и планшетах. Причин этому несколько, но главная — ощущения не те, особенно при кривой работе генератора случайных чисел, когда появляется сильное желание запустить девайс об стену.
Несмотря на то, что Dungeons&Dragons на данный момент меньше 40 лет, некубические игральные кости намного старше.
Встречайте — ~~ископаемый баян~~ кость d20 из Древнего Египта. Возрастом в пару тысячелетий. Так как привычных нам арабских цифр к моменту изготовления туда привезти не успели, то грани обозначены буквами греческого алфавита. Хранится в музее Metropolitan Museum of Art.

В рассматриваемом наборе к классической семёрке добавлены ещё d24, d30 и дополнительный экземпляр d10.
Отличия между тремя d10 заключается в том, что один несёт на себе цифры от 0 до 9, второй — от 1 до 10, а третий — десятки от 00 до 90. Это позволяет заменить броском 2d10 бросок 1d100, чтобы получить в результате значение процентов.
Да, такое тоже встречается. Только этот кубик настолько многогранен, что уже почти шарик. В том числе и по этой причине он редко встречается — берут его обычно в качестве сувенира, потому что бросать его неудобно.

Набор пришёл в обычном пакете из тёмно-серого пластика.

В котором находился пакет с защёлкой. Вообще этот набор делается в восьми цветовых исполнениях — чёрном, белом, красном, синем, зелёном, жёлтом, коричневом и фиолетовом.

Содержимое пакета.
Дальний ряд, слева направо — d4, d6, d8, d10(1-10), d10(0-9).
Ближний ряд, слева направо — d10(00-90), d12, d20, d24, d30.

Маркировка граней выполнена залитием углублений краской. Цифры нанесены аккуратно, резкий запах не обнаружен.
Грани закруглены для лучшего качения по столу. Из-за этого кости, особенно начиная с d12, легко укатываются. Для того, чтобы не ловить их потом по всей комнате (и чтобы отдельные личности не жульничали при бросках), придумано приспособление под названием «dice tower». Тоже, кстати, не новинка — в музеях есть экземпляры возрастом за полторы тысячи лет.

В ассортименте магазина оно тоже есть.

Только 10 долларов за несколько кусков оргстекла — на мой взгляд, многовато.
Тем более что под руками есть упаковка от рулонной шторы.

Берём маркер с тонким носиком и размечаем. Сплошная линия — линия разреза, штриховая линия — линия сгиба.

После резки и сгибания.

Ещё детали.

В окончательно собранном виде.

Видео использования можно просмотреть вот тут.

mysku.ru

Что внутри у круглого кубика

Все вы, наверное, сталкивались с игральными кубиками, на гранях которых расположены точки от 1 до 6.
Возможно, вы даже видели «кубики», а точнее, игральные кости, имеющие другое число граней, например, правильный додекаэдр имеет 12 граней, а правильный икосаэдр — 20 граней.
Но самая удивительная штука — круглый кубик!

На нём, как и на обычном кубике, есть точки от 1 до 6, и этот совершенно круглый «кубик» ухитряется останавливаться не как попало, а именно точками вверх.
Как же ему это удаётся?

Круглый игральный кубик и 12-гранник (додекаэдр) — см на фото выше.

голубой 100-гранный кубик,
тёмно-синий 4-гранный «кубик», а точнее пирамидка или тетраэдр,
белый 8-гранный «кубик», точнее, октаэдр,
фиолетовый 20-гранный «кубик» — икосаэдр.

Додекаэдр — 12-гранник

Круглый «кубик», который всё-таки останавливается именно 6 точками вверх.

Возможно, внутри этого круглого кубика катается грузик?
Ну-ка, потрясём немного этот круглый «кубик».

Так и есть!
Внутри есть грузик, и он катается, а потом останавливается в одном из 6 положений.
Значит,

Как же он всё-таки устроен, этот круглый «кубик»??

Подумайте ещё немного!

Ну что, сдаётесь?

pgbooks.ru

Что внутри у круглого кубика

Круглый игральный кубик и 12-гранник (додекаэдр) — см на фото выше.

Додекаэдр — 12-гранник

Круглый «кубик», который всё-таки останавливается именно 6 точками вверх.

Возможно, внутри этого круглого кубика катается грузик?
Ну-ка, потрясём немного этот круглый «кубик».

Так и есть!
Внутри есть грузик, и он катается, а потом останавливается в одном из 6 положений.
Значит,

Как же он всё-таки устроен, этот круглый «кубик»??

Подумайте ещё немного!

Ну что, сдаётесь?

pgbooks.ru

Кубики и Вероятности

В настольных и кабинетных играх для генерации случайных чисел зачастую используются игральные кубики. Однако часто для разработки сбалансированной игры требуется получить более сложные распределения случайных величин, чем линейное, задаваемое одной игральной костью. Более того, порой требуется задать распределение в определенных числовых рамках и точно знать, какова вероятность выпадения того или иного значения.

Чтобы упростить себе разработку и балансировку игр в вышеописанных ситуациях, я в свое время создал для себя небольшую шпаргалку. Думаю, что такая подсказка может пригодиться как начинающим разработчикам, так и активным игрокам. Поэтому в данной статье я поделюсь своими расчетами, а так же методом, при помощи которого можно высчитывать вероятности для любых комбинаций игральных костей.

Общая вводная

Для начала я бы хотел немного раскрыть терминологию, которая будет использована в дальнейшем.

Исторически сложилось, что бросок игральной кости обозначается как XdY, где X — количество бросков, а Y — число граней или иное маркирование типа кости. Например 1d6 означает 1 бросок 6-гранного кубика. Буква d означает dice (мн. ч. от die — игральная кость, кубик (англ.)). Закоренелые игроки так и называют игровые кости — дайсы. Впрочем, иногда встречается и русский вариант записи — 1к6. Лично я предпочитаю использовать слово дайс, поскольку «кубик» у меня строго ассоциируется с 6-гранником 🙂

Соответственно, сам дайс в такой системе обозначается как dY. Так что если вам вдруг встретится запись вида d6, знайте, что это просто 6-гранный кубик. А запись 2d10 означает «результат двух бросков 10-гранного дайса».

Джентльменский набор дайсов

В качестве d2 может использоваться обыкновенная монета. Наиболее часто встречаются следующие форматы дайсов: d4, d6, d8, d10, d12, d20. Реже можно встретить d30. Особые ухищрения позволяют моделировать d100 с помощью двух d10, однако наибольшее распространение получил, конечно же, d6.

В некоторых старых компьютерных играх можно встретить такие интересные обозначения как 1d3 или 3d17. Естественно, представить себе 17-гранный кубик немного проблематично, так что, по сути дела, это — своеобразный переходный артефакт, когда компьютер уже позволял задавать случайное распределение в любом диапазоне, но игроки по старой привычке ориентировались по дайсовой схеме. В современных компьютерных играх обычно указан разброс случайных значений в формате X-Y. Например 15-85, что означает случайное значение от 15 до 85.

Впрочем, нас сейчас интересуют дайсы, так что вернемся к ним. Дайсовая форма записи имеет небольшое преимущество над записью формы X-Y. Хоть по-сути 2d6 означает случайную величину от 2 до 12, но в случае записи 2-12 нам неведом график распределения между этими значениями. Т.е. мы не знаем, одинакова ли вероятность выпадения, например 7 и 10. 2d6, в свою очередь, подразумевает не только границу значений 2-12, но и определенный порядок распределения случайных величин, о чем и пойдет речь далее.

Осталось добавить, что для смещения диапазона значений используются так называемые модификаторы броска. Фактически, это просто число, которое прибавляется или вычитается из результата броска. Записывается это в форме XdY+Z, где Z — и есть модификатор. Например, 1d6+3 означает 1 бросок 6-гранного кубика, к результату которого прибавляется 3.

С обозначениями разобрались, можно двигаться дальше.

1d6

В качестве подопытного возьмем знаменитый d6. При необходимости расчеты для любых других вариантов (включая экзотические d17) делаются без особых затруднений по аналогии. Главное — понять принцип.

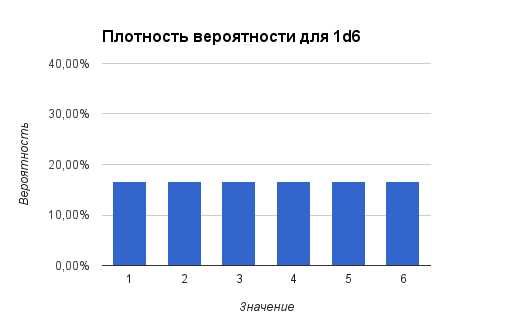
Сначала проанализируем плотность вероятностей для броска 1d6.
Плотность вероятностей в нашем случае — это шанс выпадения тех или иных значений на кубике.

Очевидно что вероятность кубика упасть на ту или иную грань, в случае когда у нас идеально сбалансированный и не крапленый кубик, обратно-пропорциональна количеству его граней. Для d6 она, соответственно, составляет 1/6 или 16,67%. Т.е. любое из 6 значений выпадает с равной вероятностью в 16,67%.

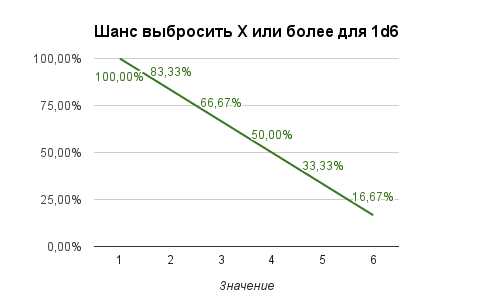
Порою весьма полезно бывает знать какова вероятность выбросить значение равное или превышающее какое-то число. Кстати, такое значение принято записывать как X+. Например, 4+ означает «4 и более». Впрочем, к обозначению 18+ уже многие привыкли, так что освоиться с такой записью не составляет никакого труда 🙂

Посчитать такую вероятность довольно просто. Достаточно просуммировать вероятности всех удовлетворяющих нас результатов. Например в случае 5+ для 1d6 нас интересует сумма шансов выбросить 5 и 6. А это 1/6+1/6=1/3 или 16,67%+16,67% = 33,33% (Все процентные значения указаны с округлением. На самом деле 16,67% это 16,666666…..6%. Поэтому не удивляйтесь тому, что иногда 7+7=13 🙂 ).

Таким образом получаем следующие графики:

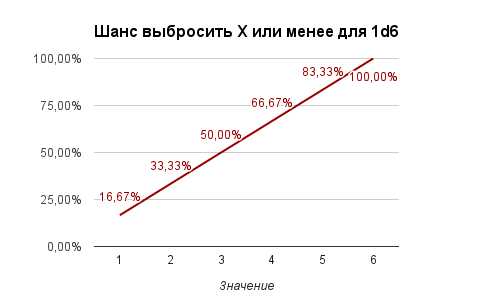
Если свести все полученные данные в таблицу, то получим:

Значение	Вероятность	Значение	Вероятность	Значение	Вероятность
1	16,67%	1+	100,00%	1	16,67%
2	16,67%	2+	83,33%	2-	33,33%
3	16,67%	3+	66,67%	3-	50,00%
4	16,67%	4+	50,00%	4-	66,67%
5	16,67%	5+	33,33%	5-	83,33%
6	16,67%	6	16,67%	6-	100,00%

Ничего необычного. Для любого единичного броска кубика с любым количеством граней мы будем получать равномерное линейное распределение. Но что будет, если мы будем рассматривать результат нескольких бросков?

2d6

Проанализируем плотность вероятностей для 2d6. Для этого нам потребуется составить матрицу, столбцы которой будут результатами первого броска, а строки — второго.

Теперь нам нужно высчитать вероятности всех возможных исходов при двух бросках и записать их в ячейки матрицы. Если вероятность выбросить на d6 1 равна 1/6, то вероятность получить 1 и во втором броске равна 1/6 от 1/6, то есть 1/36 или 2,78%.

Таким образом в каждой ячейке такой матрицы получаем значение 2,78%

	1	2	3	4	5	6
1	2,78%	2,78%	2,78%	2,78%	2,78%	2,78%
2	2,78%	2,78%	2,78%	2,78%	2,78%	2,78%
3	2,78%	2,78%	2,78%	2,78%	2,78%	2,78%
4	2,78%	2,78%	2,78%	2,78%	2,78%	2,78%
5	2,78%	2,78%	2,78%	2,78%	2,78%	2,78%
6	2,78%	2,78%	2,78%	2,78%	2,78%	2,78%

Однако если мы заполним ту же самую матрицу значениями, которые получаются в сумме двух бросков, то получим:

	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Из таблицы видно, что к значению 2 от броска 2d6 ведет только 1 исход, когда оба броска показали 1. В то время как получить 4 можно одним из трех исходов: 3 и 1, 2 и 2, 1 и 3. Выходит, что вероятность получить 4 при броске 2d6 равна сумме вероятностей 3 исходов, вероятность каждого из которых равна 2,78%. Получаем 2,78%+2,78%+2,78%=8,33% (помним про округление процентов).

Если составить таблицу вероятности для всех значений, получим:

Значение	Вероятность
2	2,78%
3	5,56%
4	8,33%
5	11,11%
6	13,89%
7	16,67%
8	13,89%
9	11,11%
10	8,33%
11	5,56%
12	2,78%

В графическом представлении это выглядит так:

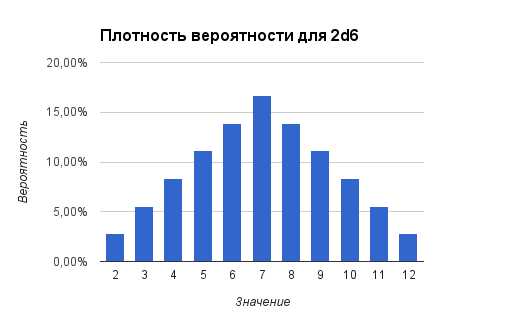
Заметим, что при учете двух бросков мы получаем распределение Гаусса (оно же нормальное распределение). Вероятность получить в результате двух бросков срединное значение (в нашем случае это 7) значительно выше, чем вероятность получить крайние значения (2 или 12). Соответственно гораздо чаще результаты бросков для 2d6 будут находится среди значений 5-9 и редко показывать 2-4 или 10-12. В некоторых случаях от случайной величины требуется именно такое поведение.

Кривые вероятности выбросить значение X+ или X- так же будут иметь нелинейный вид:

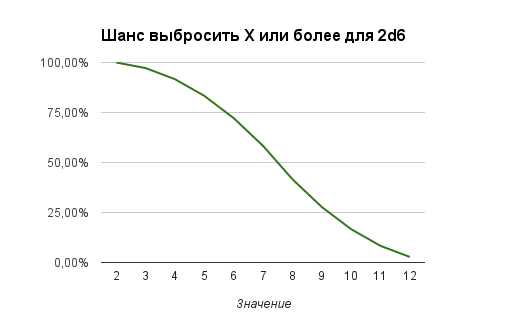
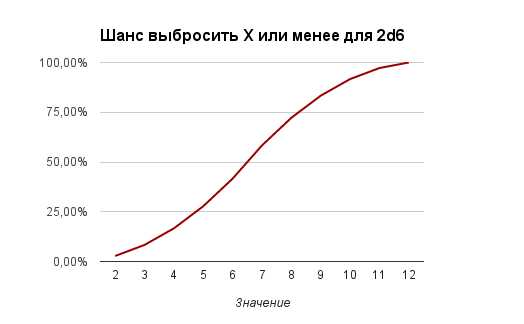
Если представить полученные данные в табличной форме, то:

Значение	Вероятность	Значение	Вероятность	Значение	Вероятность
2	2,78%	2+	100,00%	2	2,78%
3	5,56%	3+	97,22%	3-	8,33%
4	8,33%	4+	91,67%	4-	16,67%
5	11,11%	5+	83,33%	5-	27,78%
6	13,89%	6+	72,22%	6-	41,67%
7	16,67%	7+	58,33%	7-	58,33%
8	13,89%	8+	41,67%	8-	72,22%
9	11,11%	9+	27,78%	9-	83,33%
10	8,33%	10+	16,67%	10-	91,67%
11	5,56%	11+	8,33%	11-	97,22%
12	2,78%	12	2,78%	12-	100,00%

Получается, что если мы хотим получить генератор случайных чисел, который выдает распределение близкое к тому, что встречается «в природе», то использование пары кубиков или учет двух бросков дает нам эту возможность.

Ровно как и запись 2d6 имеет преимущество над 2-12 как раз в том, что указывает не только на диапазон, но и на плотность вероятностей.

Если же нам требуется получить нормальное распределение в промежутке от 0 до 10, то с помощью дайсов это можно организовать как бросок 2d6 из результата которого будем вычитать 2. Вспоминая описанные ранее обозначения, это 2d6-2.

Если такая перемена в графике произошла когда мы добавили второй бросок, то что произойдет, если ввести третий?

3d6

Для анализа плотности вероятностей для 3d6 можно, конечно составить 3-х мерную матрицу и посчитать все точь-в-точь как для 2d6. Но поскольку вероятности для 2d6 нам уже известны, то мы можем значительно упростить себе задачу:

	2d6	1	2	3	4	5	6
2	2,78%
3	5,56%
4	8,33%
5	11,11%
6	13,89%
7	16,67%
8	13,89%
9	11,11%
10	8,33%
11	5,56%
12	2,78%

Помножив вероятности результатов для 2d6 на 16,67% получим вероятности исходов для 3-х бросков:

	2d6	1	2	3	4	5	6
2	2,78%	0,46%	0,46%	0,46%	0,46%	0,46%	0,46%
3	5,56%	0,93%	0,93%	0,93%	0,93%	0,93%	0,93%
4	8,33%	1,39%	1,39%	1,39%	1,39%	1,39%	1,39%
5	11,11%	1,85%	1,85%	1,85%	1,85%	1,85%	1,85%
6	13,89%	2,31%	2,31%	2,31%	2,31%	2,31%	2,31%
7	16,67%	2,78%	2,78%	2,78%	2,78%	2,78%	2,78%
8	13,89%	2,31%	2,31%	2,31%	2,31%	2,31%	2,31%
9	11,11%	1,85%	1,85%	1,85%	1,85%	1,85%	1,85%
10	8,33%	1,39%	1,39%	1,39%	1,39%	1,39%	1,39%
11	5,56%	0,93%	0,93%	0,93%	0,93%	0,93%	0,93%
12	2,78%	0,46%	0,46%	0,46%	0,46%	0,46%	0,46%

Ну а просуммировав исходы с одинаковым результатом, получим плотности вероятностей:

Значение	Вероятность
3	0,46%
4	1,39%
5	2,78%
6	4,63%
7	6,94%
8	9,72%
9	11,57%
10	12,50%
11	12,50%
12	11,57%
13	9,72%
14	6,94%
15	4,63%
16	2,78%
17	1,39%
18	0,46%

Графически это выглядит так:

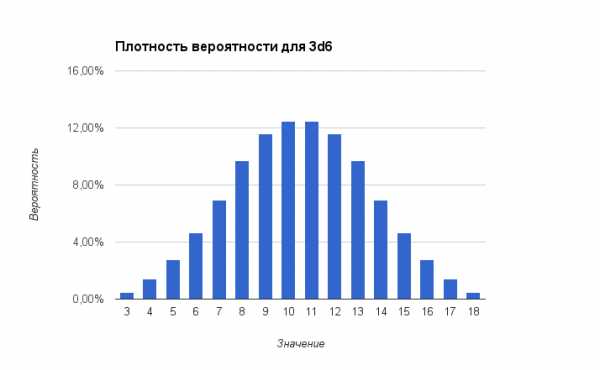
Графики вероятностей для X+ и X- тоже имеют более выраженные очертания нормального распределения:

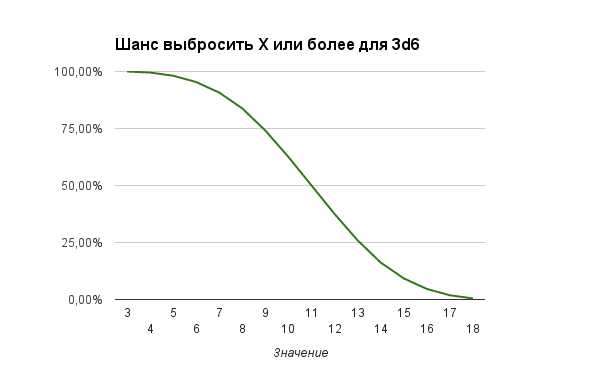
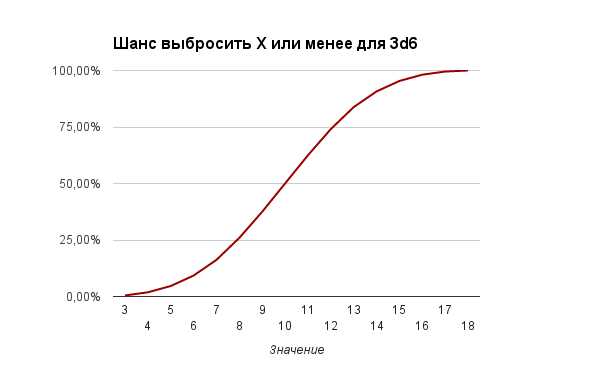
Итоговая таблица для 3d6 будет выглядеть так:

Значение	Вероятность	Значение	Вероятность	Значение	Вероятность
3	0,46%	3+	100,00%	3	0,46%
4	1,39%	4+	99,54%	4-	1,85%
5	2,78%	5+	98,15%	5-	4,63%
6	4,63%	6+	95,37%	6-	9,26%
7	6,94%	7+	90,74%	7-	16,20%
8	9,72%	8+	83,80%	8-	25,93%
9	11,57%	9+	74,07%	9-	37,50%
10	12,50%	10+	62,50%	10-	50,00%
11	12,50%	11+	50,00%	11-	62,50%
12	11,57%	12	37,50%	12-	74,07%
13	9,72%	13+	25,93%	13-	83,80%
14	6,94%	14+	16,20%	14-	90,74%
15	4,63%	15+	9,26%	15-	95,37%
16	2,78%	16+	4,63%	16-	98,15%
17	1,39%	17+	1,85%	17-	99,54%
18	0,46%	18	0,46%	18-	100,00%

Из полученных результатов видно, что с увеличением количества бросков до 3 «колокол Гаусса» не только сохраняется, но и становиться более выраженным. Забегая вперед скажу что и для всех последующих повышений количества бросков (4d6, 5d6, 6d6 …) эта тенденция сохраняется.

Вместо итогов

Полученные таблицы можно использовать для балансировки вероятностных значений в разрабатываемых играх. Ровно как можно с помощью данных расчетов более точно оценивать свои шансы на исход броска во время игры.

Продемонстрированный метод применим для получения таблиц к любому количеству бросков любых дайсов.

Кстати, с помощью разнообразных дайсов можно задавать довольно большой диапазон случайных значений. Например 2d6+1d4 даст нормальное распределение в диапазоне 3-16. А с помощью двух d10 можно задать линейное распределение 0-99, для этого один кубик должен отвечать за десятки, другой — за единицы. Такую комбинацию двух d10 называют «процентником».

Надеюсь, эти таблицы будут Вам полезны.

Юрий Исаев
2015.07.27

ulf.tordenson.ru

Женский волейбольный клуб «ДИНАМО-МЕТАР»