100 метров 9 класс: Труба из сшитого полиэтилена Rehau RAUTITAN Stabil PLATINUM 20x2,9 мм, 100 метров купить в Москве

Содержание

Таблица перевода единиц измерения

Длина

1 см = 10 мм = 0,01 м

1 дм = 10 см = 0,1 м

1 м = 100 см = 10 дм

1 км = 1000 м

1 дюйм (inch) = 2.54 см

1 фут (foot) = 12 дюймов = 30,48 см = 0,3048 м

1 ярд (yard)= 3 фута = 91,44 см = 0,9144 м

1 миля (mile) = 5280 футов = 1609,34 м = 1,609 км

1 морская миля (nautical mile) =1,852 км

1 м = 3,28 фута = 1,094 ярда = 0,00062 мили

1 см = 0,393 дюйма

Площадь

1 см² = 100 мм²

1 дм² = 100 см² = 0,01 м²

1 м² = 100 дм²

1 км² = 1 000 000 м²

1 ар (1 а) = 100 м² = 1 сотка

1 гектар (1 га) = 10 000 м²

1 кв.

дюйм (square inch) = 6,4516 см²

1 кв. фут (square foot) = 144 кв. дюймам = 929,03 см²

1 кв. ярд (square yard) = 9 кв. футам = 0,83613 м²

1 акр (acre) = 4046,86 м²

1 кв. миля (square mile) = 640 акрам = 2,59 км²

1 м² = 10,76 кв. футов = 1,196 кв. ярдов

1 см² = 0,155 кв. дюймов

Объем

1 см³ = 0,001 дм³ = 0,001 л

1 литр = 1 дм³ = 61,03 куб. дюйм = 0,22 галлона

1 куб. дюйм = 16,387 см³ = 0,016 л

1 куб.

фут = 28316,8 см³ =28,316 л

1 куб. ярд = 764555 см³ = 764,555 л

1 пинта англ. = 0,568 л

1 пинта амер. = 0,473 л

1 галлон англ. = 4,54 л

1 галлон амер. = 3,78 л

1 баррель нефти =42 галлона = 158,988 л = 0,136 тонн

Вес

1 кг = 1000 г

1 ц = 100 кг = 0,1 т

1 т = 1000 кг = 10 ц

1 фунт = 453,6 г = 0,4536 кг

1 унция = 1/16 фунта = 28,35 г

1 г = 0,035 унций = 0,002205 фунтов

1 кг = 2,2 фунта

Тройская система мер для благородных металлов и драгоценных камней

1 гран = 64,8 мг

1 карат = 3,086 грана = 0,2 г

1 тройская унция = 31,10 г = 1/12 тр.

фунта = 480 гран

1 тройский фунт = 373,24 г

Температура

40°С = 104 F; 0°С= 32 F

F = (°C *1.8)+32

°C = (F — 32)/1,8

Разница температур в 1 °C эквивалентна разнице температур в 1,8 F

Как найти Масштаб в Математике?

Статья находится на проверке у методистов Skysmart.

Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие масштаба

Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.

Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.

Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.

Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.

Масштаб бывает трех видов:

численный, выражается в числах 1:1000;
именованный, выражается словами, то есть см переводим в
м: в 1см 10м, 10м — это величина масштаба;
линейный, зная величину масштаба, можно определить расстояния.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Определение масштаба на карте

На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.

Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.

Масштаб — это отношение размера изображения к размеру изображаемого объекта.

Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.

На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.

Численные масштабы карт и соответствующие им масштабы на местности:

Масштаб 1 : 100 000

1 мм на карте — 100 м (0,1 км) на местности
1 см на карте — 1000 м (1 км) на местности
10 см на карте — 10000 м (10 км) на местности

Масштаб 1 : 10000

1 мм на карте — 10 м (0,01 км) на местности
1 см на карте — 100 м (0,1 км) на местности
10 см на карте — 1000 м (1 км) на местности

Масштаб 1 : 5000

1 мм на карте — 5 м (0,005 км) на местности
1 см на карте — 50 м (0,05 км) на местности
10 см на карте — 500 м (0,5 км) на местности

Масштаб 1 : 2000

1 мм на карте — 2 м (0,002 км) на местности
1 см на карте — 20 м (0,02 км) на местности
10 см на карте — 200 м (0,2 км) на местности

Масштаб 1 : 1000

1 мм на карте — 100 см (1 м) на местности
1 см на карте — 1000 см (10 м) на местности
10 см на карте — 100 м на местности

Масштаб 1 : 500

1 мм на карте — 50 см (0,5 метра) на местности
1 см на карте — 5 м на местности
10 см на карте — 50 м на местности

Масштаб 1 : 200

1 мм на карте — 0,2 м (20 см) на местности
1 см на карте — 2 м (200 см) на местности
10 см на карте — 20 м (0,2 км) на местности

Масштаб 1 : 100

1 мм на карте — 0,1 м (10 см) на местности
1 см на карте — 1 м (100 см) на местности
10 см на карте — 10м (0,01 км) на местности

Решение задач на масштаб

Для закрепления темы решим несколько математических задач на масштаб за 6 класс.

Пример 1. Длина отрезка на карте равна 8 см. Найти длину соответствующего отрезка на местности, если масштаб карты равен 1 : 10 000.

Как решаем:

8 см — это 1 часть

8 * 10 000 = 80 000 (см) — это 10 000 частей

80 000 см = 800 м

Ответ: 800 м

Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.

Как решаем:

400 км = 400 000 м = 40 000 000 см

40000000 : 5000000 = 40 : 5 = 8

Ответ: 8 см

Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?

Как решаем:

700 км = 700 000 м = 70 000 000 см

70 000 000 : 14 = 5 000 000

Ответ: уменьшить в 5 000 000 раз.

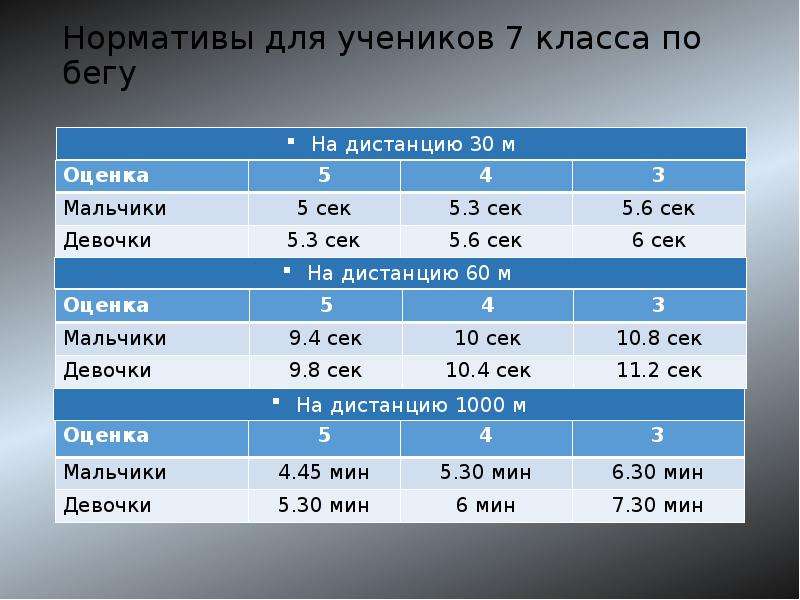
Физическая культура. 9 класс. Бег на 100 м. Техника выполнения.

Конспект урока

Конспект на интерактивный видео-урок по предмету «Физическая культура» для «10» класса

Урок № 4. Бег на 100 метров – техника выполнения

Перечень вопросов, рассматриваемых в теме

В теоретической части представлены:

· беговые упражнения;

· техника бега на 100 м.

Урок посвящён технике выполнения бега на 100 м и беговым подготовительным упражнениям.

Глоссарий

Физическое упражнение – набор упорядоченных движений, составленных в двигательное действие.

Стойка – статичное положение тела.

Атлетика – совокупность упражнений, направленная на развитие силы и выносливости человека.

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ

Любая тренировка начинается с разминки, чтобы не получить травму. Выполнив легкую пробежку, приступим к нескольким беговым упражнениям.

Бег с высоко поднятыми коленями

Встаньте прямо, руки перед собой на уровне пояса ладонями вниз, спина прямо. Начинайте движение вперёд так, чтобы при каждом шаге колено коснулось ладони.

Захлёсты голени

Встаньте прямо, руки на пояс, спина прямо. Начинайте движение вперёд и с каждым шагом пятка должна касаться ягодицы, а колено смотрит вниз.

Выпады

Встаньте прямо, руки на поясе или как вам удобней для удержания равновесия, спина прямо. Сделайте шаг вперёд и опуститесь вниз так, чтобы передняя нога в коленном суставе образовывала угол 90 градусов. Вернитесь в исходное положение и повторите шаг с другой ноги.

Выпрыгивания

Встаньте прямо, руки за головой или так, как вам проще удержать равновесие и выполнить прыжок, спина прямо. Сделайте приседание и во время подъема подпрыгните.

Чтобы добиться лучшего результата в спринте, очень важно после старта быстрее достичь в фазе стартового разбега скорости, близкой к максимальной

Бег по дистанции

К моменту достижения высшей скорости туловище бегуна незначительно (72—80°) наклонено вперёд. В течение бегового шага происходит изменение величины наклона. Во время отталкивания наклон туловища уменьшается, а в полетной фазе он увеличивается.

Начало бега (старт)

В спринте применяется низкий старт, позволяющий быстрее начать бег и развить максимальную скорость на коротком отрезке. По команде «На старт!» бегун становится впереди колодок, приседает и ставит руки впереди стартовой линии. По команде «Внимание!» бегун слегка выпрямляет ноги, отделяет колено сзади стоящей ноги от дорожки. Услышав выстрел (или другой стартовый сигнал), бегун мгновенно устремляется вперёд.

Финиширование

Максимальную скорость в беге на 100 и 200 м необходимо стараться поддерживать до конца дистанции, однако на последних 20—15 м дистанции скорость обычно снижается на 3—8%. Бег заканчивается в момент, когда бегун коснется туловищем вертикальной плоскости, проходящей через линию финиша.

Вертикальное строение атмосферы

Тропосфера

Её верхняя граница находится на высоте 8—10 км в полярных, 10—12 км в умеренных и 16—18 км в тропических широтах; зимой ниже, чем летом. Нижний, основной слой атмосферы содержит более 80 % всей массы атмосферного воздуха и около 90 % всего имеющегося в атмосфере водяного пара. В тропосфере сильно развиты турбулентность и конвекция, возникают облака, развиваются циклоны и антициклоны. Температура убывает с ростом высоты со средним вертикальным градиентом 0,65°/100 м

Тропопауза

Переходный слой от тропосферы к стратосфере, слой атмосферы, в котором прекращается снижение температуры с высотой.

Стратосфера

Слой атмосферы, располагающийся на высоте от 11 до 50 км. Характерно незначительное изменение температуры в слое 11—25 км (нижний слой стратосферы) и повышение её в слое 25—40 км от −56,5 до 0,8 °С (верхний слой стратосферы или область инверсии). Достигнув на высоте около 40 км значения около 273 К (почти 0 °C), температура остаётся постоянной до высоты около 55 км. Эта область постоянной температуры называется стратопаузой и является границей между стратосферой и мезосферой.

Стратопауза

Пограничный слой атмосферы между стратосферой и мезосферой. В вертикальном распределении температуры имеет место максимум (около 0 °C).

Мезосфера

Мезосфера начинается на высоте 50 км и простирается до 80—90 км. Температура с высотой понижается со средним вертикальным градиентом (0,25—0,3)°/100 м. Основным энергетическим процессом является лучистый теплообмен. Сложные фотохимические процессы с участием свободных радикалов, колебательно возбуждённых молекул и т. д. обусловливают свечение атмосферы.

Мезопауза

Переходный слой между мезосферой и термосферой. В вертикальном распределении температуры имеет место минимум (около —90 °C).

Линия Кармана

Высота над уровнем моря, которая условно принимается в качестве границы между атмосферой Земли и космосом. Линия Кармана находится на высоте 100 км над уровнем моря.

Граница атмосферы Земли

Принято считать, что граница атмосферы Земли и ионосферы находится на высоте 118 километров. Это показывает анализ параметров движения высокоэнергетических частиц, перемещающихся в атмосфере и ионосфере.

Термосфера

Верхний предел — около 800 км. Температура растёт до высот 200—300 км, где достигает значений порядка 1500 К, после чего остаётся почти постоянной до больших высот. Под действием ультрафиолетовой и рентгеновской солнечной радиации и космического излучения происходит ионизация воздуха («полярные сияния») — основные области ионосферы лежат внутри термосферы. На высотах свыше 300 км преобладает атомарный кислород. Верхний предел термосферы в значительной степени определяется текущей активностью Солнца. В периоды низкой активности происходит заметное уменьшение размеров этого слоя.

Термопауза

Область атмосферы прилегающая сверху к термосфере. В этой области поглощение солнечного излучения незначительно и температура фактически не меняется с высотой.

Экзосфера (сфера рассеяния)

Атмосферные слои до высоты 120 км

Экзосфера — зона рассеяния, внешняя часть термосферы, расположенная выше 700 км. Газ в экзосфере сильно разрежен, и отсюда идёт утечка его частиц в межпланетное пространство (диссипация).

До высоты 100 км атмосфера представляет собой гомогенную хорошо перемешанную смесь газов. В более высоких слоях распределение газов по высоте зависит от их молекулярных масс, концентрация более тяжёлых газов убывает быстрее по мере удаления от поверхности Земли. Вследствие уменьшения плотности газов температура понижается от 0 °C в стратосфере до −110 °C в мезосфере. Однако кинетическая энергия отдельных частиц на высотах 200—250 км соответствует температуре ~150 °C. Выше 200 км наблюдаются значительные флуктуации температуры и плотности газов во времени и пространстве.

На высоте около 2000—3500 км экзосфера постепенно переходит в так называемый ближнекосмический вакуум, который заполнен сильно разреженными частицами межпланетного газа, главным образом атомами водорода. Но этот газ представляет собой лишь часть межпланетного вещества. Другую часть составляют пылевидные частицы кометного и метеорного происхождения. Кроме чрезвычайно разреженных пылевидных частиц, в это пространство проникает электромагнитная и корпускулярная радиация солнечного и галактического происхождения.

На долю тропосферы приходится около 80 % массы атмосферы, на долю стратосферы — около 20 %; масса мезосферы — не более 0,3 %, термосферы — менее 0,05 % от общей массы атмосферы. На основании электрических свойств в атмосфере выделяют нейтросферу и ионосферу. В настоящее время считают, что атмосфера простирается до высоты 2000—3000 км.

В зависимости от состава газа в атмосфере выделяют гомосферу и гетеросферу. Гетеросфера — это область, где гравитация оказывает влияние на разделение газов, так как их перемешивание на такой высоте незначительно. Отсюда следует переменный состав гетеросферы. Ниже её лежит хорошо перемешанная, однородная по составу часть атмосферы, называемая гомосфера. Граница между этими слоями называется турбопаузой, она лежит на высоте около 120 км.

A пробежит 100 метров за 11 секунд, а B пробежит 100 метров класс 9 по математике CBSE

Подсказка: Сначала рассчитайте скорость A и B, используя формулу скорости, а затем рассчитайте расстояние, пройденное A и B за 11 секунд.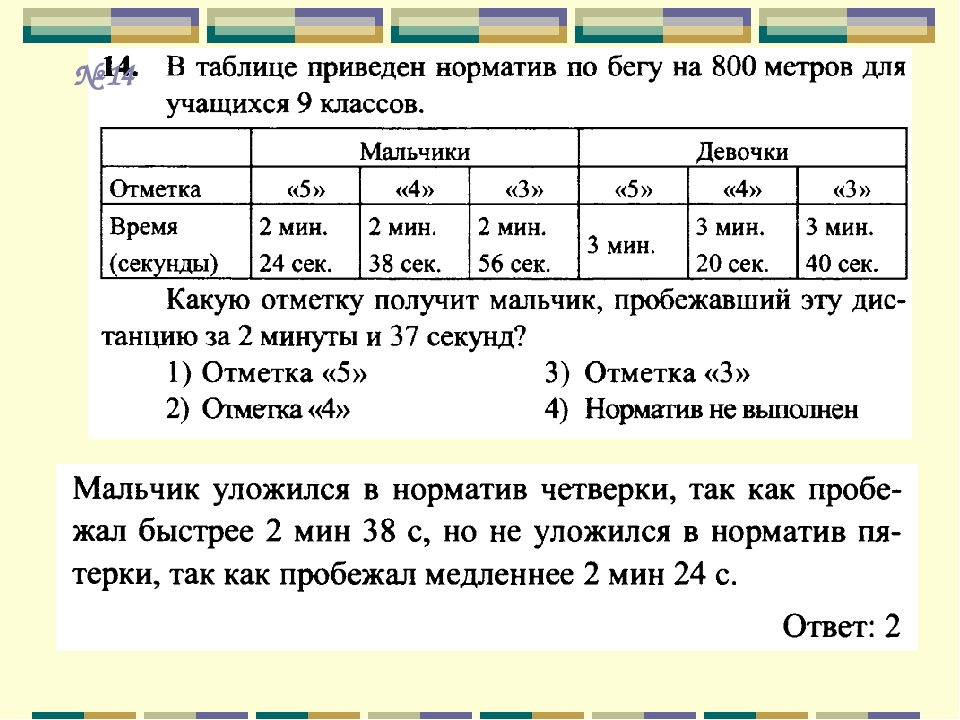

Используемая формула: Запомните треугольник расстояния, скорости и времени. Если вы хотите вычислить скорость, то положите большой палец на «s», останется $\dfrac{d}{t},$, что станет формулой для скорости. Аналогично для расстояния и времени.

Полный пошаговый ответ:

Расстояние, пройденное A = 100 м
Время, затраченное A = 11 секунд
Скорость A , S A = $\dfrac{{distance}}{{time}}$
Подставьте значение расстояния и времени в эту формулу.
$ = \dfrac{{100}}{{11}}м/с$
Расстояние, пройденное B = 100 м
Время, затраченное B = 12 секунд
Подставьте значение расстояния и времени в эту формулу.
Скорость B, SB = \[\dfrac{{расстояние}}{{время}}\]
\[ = \dfrac{{100}}{{12}}м/с\]
Теперь, чтобы сделать Жеребьевка гонки означает, что оба должны завершить гонку одновременно за 11 секунд.
Расстояние, пройденное A за 11 секунд, = скорости A(S A ) времени
Подставьте значения скорости и времени в эту формулу.

=$\dfrac{{100}}{{11}} \times 11$
$ = 100м$
Расстояние, пройденное B за 11 секунд
= скорость B(SB ) во времени
=$\dfrac{{100} }{{12}} \times 11m$
$ = \dfrac{{1100}}{{12}}m$
$ = 91\dfrac{8}{{12}}$m
$ = 91\dfrac{ 2}{3}m$
$\,\,\,\,начало\,\,из B=\left( {100 — \dfrac{{1100}}{{12}}m} \right )$
\[ = \dfrac{{1200{\text{ — }}1100}}{{12}}\]m
$ = \dfrac{{100}}{{12}}m$
$ = 8 \dfrac{4}{{12}}$m
$ = 8\dfrac{1}{3}m$ необходимо передать B, чтобы гонка завершилась за 11 секунд.
Следовательно, B должен стартовать со стартом $8\dfrac{1}{3}m$, чтобы гонка завершилась за 11 секунд.

Примечание: При решении задач такого типа не забудьте указать соответствующие единицы скорости и времени в окончательном ответе. два, которые дадут окончательный ответ.

Лахмир Сингх Физика, 9 класс, Solutions Motion

Справочник по формулам для 9 класса, математика и естественные науки

Лахмир Сингх Физика Класс 9 Solutions Motion

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 19

Вопрос 1:
Является ли смещение скалярной величиной?
Решение:
Нет, перемещение является векторной величиной.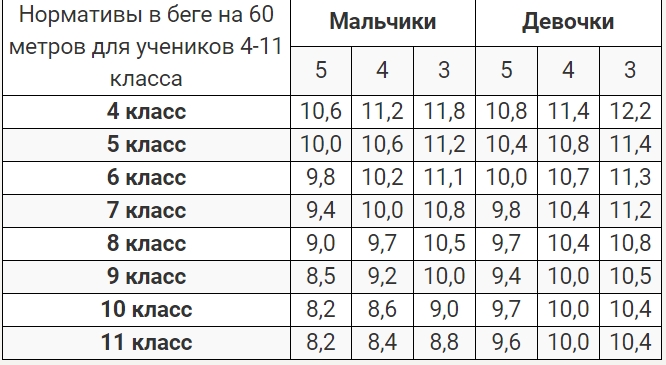

Вопрос 2:
Укажите, является ли расстояние скалярной или векторной величиной.
Решение :
Расстояние является скалярной величиной.

Вопрос 3:
Измените скорость 6 м/с на км/ч.
Решение:
6 м/с
= 6 x (3600/1000) км/ч = 21,6 км/ч

Вопрос 4:
Как называется скорость в указанном направлении?
Решение :
Скорость тела в заданном направлении называется скоростью.

Вопрос 5:
Приведите два примера тел, движущихся неравномерно.
Решение:
(a) Движение автобуса по дороге
(b) Движение скаковой лошади

Вопрос 6:
Назовите физическую величину, полученную путем деления «Пройденного расстояния» на «Время, затраченное на преодоление этого расстояния».
Решение :
Скорость определяется как расстояние, пройденное за единицу времени.

Вопрос 7:
Какие следующие измерения в автомобиле?
(a) Спидометр (b) Одометр
Решение:
(a) Спидометр автомобиля измеряет мгновенную скорость автомобиля.
(b)Одометр – это устройство, используемое для регистрации расстояния, пройденного автомобилем.

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 20

Вопрос 8:
Назовите физическую величину, которая дает нам представление о том, насколько быстро или медленно движется тело.
Решение :
Скорость дает представление о том, насколько быстро или медленно движется тело.

Вопрос 9:
При каких условиях тело может пройти определенное расстояние и при этом его результирующее перемещение будет равно нулю?
Решение:
Когда тело возвращается в исходную точку, оно имеет нулевое результирующее перемещение, но проходит некоторое ненулевое расстояние.

Вопрос 10:
Что еще нужно знать, кроме скорости, чтобы предсказать положение движущегося тела?
Решение:
Помимо скорости, мы должны знать направление, в котором движется тело.

Вопрос 11:
Когда говорят, что тело имеет постоянную скорость?
Решение:
Когда тело проходит равные расстояния за равные промежутки времени в определенном направлении, каким бы малым или большим ни был временной интервал, говорят, что тело имеет постоянную скорость.

Вопрос 12:
При каком условии величина средней скорости равна средней скорости ?
Решение:
Когда объект движется по одной прямой, величина средней скорости равна средней скорости.

Вопрос 13:
Что из двух может быть 0 при определенных условиях: средняя скорость движущегося тела или средняя скорость движущегося тела?
Решение :
Средняя скорость движущегося тела может быть равна нулю.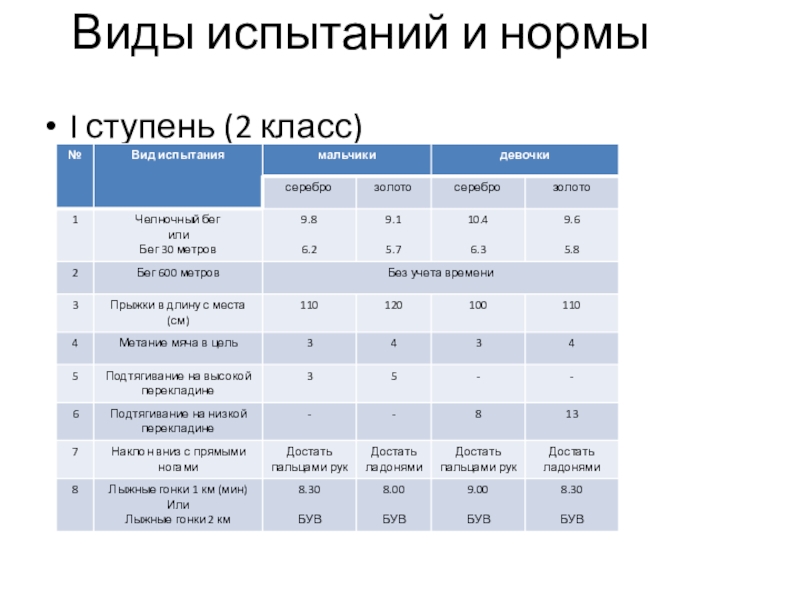

Вопрос 14:
Приведите пример ситуации, когда тело имеет некоторую среднюю скорость, но его средняя скорость равна нулю.
Решение :
Движение мальчика из дома в магазин (в одном направлении) и обратно домой (в обратном направлении) является примером ситуации, когда тело имеет некоторую среднюю скорость, но его средняя скорость равна нуль.

Вопрос 15:
Каково ускорение тела, движущегося с постоянной скоростью?
Решение:
Когда тело движется с постоянной скоростью, его ускорение равно нулю.

Вопрос 16:
Как иначе называется отрицательное ускорение?
Решение:
Отрицательное ускорение также называют замедлением.

Вопрос 17:
Назовите физическую величину, единицей СИ которой является:
(a) м/с (b) м/с ²
Решение:
(a) Скорость (или Скорость)
(b) Ускорение

Вопрос 18:
Какой тип движения демонстрирует свободно падающее тело?
Решение:
Равноускоренное движение

Вопрос 19:
Что такое единица замедления в системе СИ?
Решение:
С.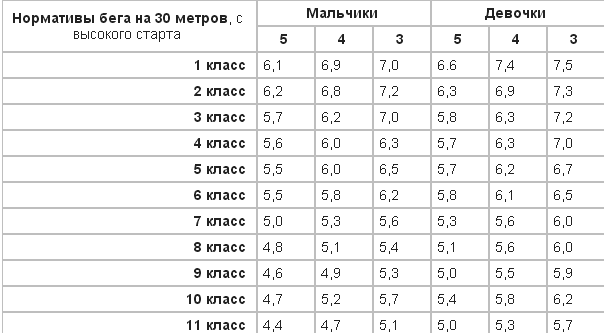 I. единица замедления м/с ² .

Вопрос 20:
Заполните следующие пропуски подходящими словами:
(a) Перемещение – это …………………… величина, тогда как расстояние – это…………………………….
(б) Физическая величина, определяющая как скорость, так и направление движения тела, называется его…………………………..
(в) Мотоцикл имеет устойчивую……………. 3 м/с ² . Это означает, что каждый………………. его …………….. увеличивается на ………….
(d) Скорость – это скорость изменения ……………………… Измеряется в .
(e) Ускорение – это скорость изменения ………………. Измеряется в
Решение :
(а) вектор, скаляр
(б) скорость
(в) ускорение, секунда, скорость, 3м/с
(г) перемещение, м/с
(д) скорость, м /с ²

Вопрос 21:
Какое движение, равномерное или неравномерное, совершает свободно падающее тело? Обоснуйте свой ответ.
Решение:
Свободно падающее тело имеет неравномерное движение, потому что оно преодолевает меньшие расстояния в начальные интервалы «1 секунда» и большие расстояния в более поздние интервалы «1 секунда», т.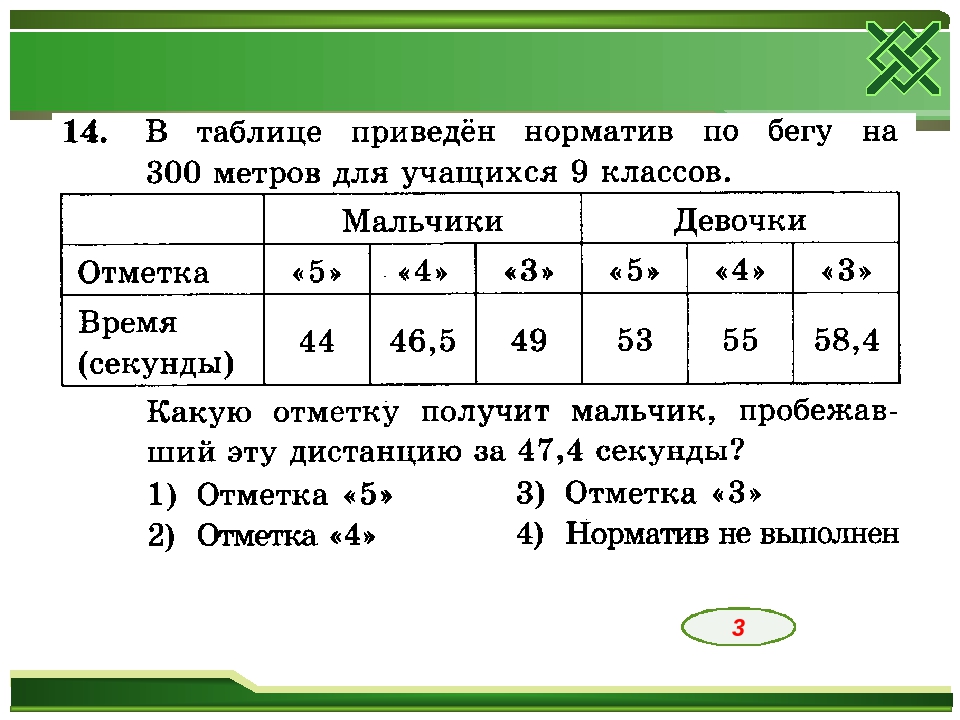 е.е., преодолевает неравные расстояния за равные промежутки времени.

Вопрос 22:
Укажите, является ли скорость скалярной или векторной величиной. Обоснуйте свой выбор.
Решение :
Скорость является скалярной величиной, так как имеет только величину, а не направление.

Вопрос 23:
Автобус X проезжает расстояние 360 км за 5 часов, тогда как автобус Y проезжает расстояние 476 км за 7 часов. Какой автобус
едет быстрее?
Решение:
Для автобуса X,
Скорость = расстояние/время
Скорость = 360/5=72 км/ч
Для автобуса Y,
Скорость = расстояние/время
Скорость = 476/7=68 км/ч
Скорость автобуса X больше, чем автобуса Y.Следовательно, автобус X едет быстрее.

Вопрос 24:
Расположите следующие скорости в порядке возрастания (сначала наименьшая скорость):

Спортсмен бежит со скоростью 10 м/с.
Велосипед, движущийся со скоростью 200 м/мин.
Самокат движется со скоростью 30 км/ч.

Решение:
Скорость спортсмена = 10 м/с
Скорость велосипеда = 200 м/мин = 200/60 м/с = 3,33 м/с
Скорость самоката = 30 км/ч = 30000/3600 м /с = 8.33 м/с
3,33 м/с < 8,33 м/с < 10 м/с
т. е. 200 м/мин < 30 км/ч < 10 м/с

Вопрос 25:
а) Напишите формулу ускорения. Укажите значение каждого символа, который в нем встречается.
(b) Поезд, отправляющийся с железнодорожного вокзала, достигает скорости 21 м/с за одну минуту. Найдите его ускорение.
Решение:

Вопрос 26:
а) Какой термин используется для обозначения изменения скорости во времени?
(b) Укажите одно слово, которое означает то же самое, что и «движение с отрицательным ускорением».
(c) Перемещение движущегося объекта за данный интервал времени равно нулю. Будет ли расстояние, пройденное объектом, также равно нулю? Обоснуйте свой ответ.
Решение:
(a) Ускорение
(b) Замедление
(c) Нет, потому что если тело совершает круговой путь так, что его конечное положение совпадает с начальным положением, то перемещение тела равно нулю, но пройденное расстояние не равно нулю.

Вопрос 27:
Улитка преодолевает расстояние 100 метров за 50 часов.Вычислите среднюю скорость улитки в км/ч.

Решение:
Средняя скорость = Общее пройденное расстояние / Общее затраченное время
Общее пройденное расстояние = 100 м = 0,1 км; Общее затраченное время = 50 часов
Средняя скорость = 0,1/50 = 0,002 км/ч

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 21

Вопрос 28:
Черепаха проходит расстояние 100 метров за 15 минут. Какова средняя скорость черепахи в км/ч?
Решение:
Общее расстояние = 100 м = 0.1 км
Общее затраченное время = 15 минут = 15/60 = 0,25 часа
Средняя скорость = общее пройденное расстояние / общее затраченное время
= 0,1/0,25 = 0,4 км/ч

Вопрос 29:
Если спринтер пробегает 100 метров за 9,83 секунды, рассчитайте его среднюю скорость в км/ч.
Решение:
Общее пройденное расстояние = 100 м
Общее затраченное время = 9,83 с
Средняя скорость = Общее пройденное расстояние/ Общее затраченное время
= 100/9,83 = 10,172 м/с
Средняя скорость в км/ч:
10.172 х (3600/1000) = 36,62 км/ч

Вопрос 30:
Мотоциклист едет из пункта А в В с постоянной скоростью 30 км ч ^-1 и возвращается из пункта В в А с постоянной скоростью 20 км ч ^-1 . Найдите его среднюю скорость.
Решение:

Вопрос 31:
Мотоциклист трогается с места и достигает скорости 6 м/с после движения с равномерным ускорением в течение 3 с. Каково его ускорение?
Решение:
Начальная скорость = 0 м/с
Конечная скорость = 6 м/с
Время = 3 с

Вопрос 32:
Самолет, летящий со скоростью 600 км/ч, постоянно ускоряется со скоростью 10 км/ч в секунду. Принимая скорость звука равной 1100 км/ч на высоте самолета, сколько времени потребуется, чтобы преодолеть «звуковой барьер»?
Решение:
Начальная скорость, u = 600 км/ч
Конечная скорость, v = 1100 км/ч
Ускорение = 10 км/ч/с = 600 км/ч ²
Из соотношения, a = (vu )/t
t = (vu)/a
t = (1100-600)/600 = 500/600 = 5/6 ч = 50 с

Вопрос 33:
Если автобус, движущийся со скоростью 20 м/с, подвергается постоянному замедлению со скоростью 5 м/с ² , через какое время он остановится?
Решение:
Замедление, a=-5 м/с ²
Начальная скорость, u=20 м/с
Конечная скорость, v=0 м/с
t=?

Вопрос 34:
(а) В чем разница между «расстоянием, пройденным» телом, и его «перемещением»? Объясните с помощью
схемы.
(b) Муравей проходит расстояние 8 см от P до Q, а затем проходит расстояние 6 см под прямым углом к PQ. Найдите его результирующее перемещение.
Решение:
(a) Пройденное расстояние — это фактическая длина непрямого пути, пройденного телом, тогда как перемещение относится к прямолинейному пути между начальным и конечным положениями. Например, На приведенном ниже рисунке тело движется из точки A в точку B, а затем из точки B в точку C. Здесь расстояние, пройденное телом, равно AB + BC, а перемещение равно AC.

Вопрос 35:
Дайте определение движения. Что вы понимаете под терминами «равномерное движение» и «неравномерное движение»? Объясните примерами.
(а) Определить скорость. Что такое единица скорости в СИ?
(b) Что подразумевается под (i) средней скоростью и (ii) равномерной скоростью?
Решение:
Говорят, что тело находится в движении, если его положение непрерывно изменяется относительно неподвижного объекта, взятого за точку отсчета.
Тело движется равномерно, если оно проходит равные расстояния за равные промежутки времени, какими бы малыми ни были эти промежутки времени. Например: автомобиль, движущийся с постоянной скоростью 10 м/с, будет преодолевать равное расстояние 10 м за каждую секунду, поэтому его движение будет равномерным.
Неравномерное движение: Тело движется неравномерно, если оно проходит неравные расстояния за равные промежутки времени. Например: сброс мяча с крыши высокого здания.

Вопрос 36:
(a) Дайте определение скорости. Что такое единица скорости в СИ?
(б) В чем разница между скоростью и скоростью?
(c) Переведите скорость 54 км/ч в м/с.
Решение:
(а) Скорость тела – это расстояние, пройденное им за единицу времени. Единицей скорости в СИ является м/с.
(b) (i) Средняя скорость тела равна общему пройденному расстоянию, деленному на общее время, затраченное на преодоление этого расстояния.
(ii) Равномерная скорость означает постоянную скорость движущегося тела. Тело имеет постоянную скорость, если оно проходит одинаковое расстояние за равные промежутки времени, какими бы малыми ни были эти промежутки времени.

Вопрос 37:
(a) Что означает термин «ускорение»? Укажите единицу ускорения в системе СИ.
(b) Дайте определение термину «равномерное ускорение». Приведите пример равноускоренного движения.
Решение:
(а) Скорость тела – это расстояние, пройденное им в единицу времени в заданном направлении. Единицей скорости в СИ является м/с.
( b)(i)Скорость является скалярной величиной, тогда как скорость является векторной величиной.
(ii) Скорость тела – это расстояние, пройденное им за единицу времени, тогда как скорость тела – это расстояние, пройденное им за единицу времени в заданном направлении.
(iii)Скорость всегда положительна, тогда как скорость может быть как положительной, так и отрицательной.
(c) Скорость = 54 км/ч = 54 х (1000/3600) = 15 м/с

Вопрос 38:
Расстояние между Дели и Агрой составляет 200 км. Поезд проходит первые 100 км со скоростью 50 км/ч. С какой скоростью поезд должен проехать следующие 100 км, чтобы на всем пути его средняя скорость составляла 70 км/ч?
Решение:
(a) Ускорение тела определяется как скорость изменения его скорости во времени. Единицей ускорения в системе СИ является м/с ² .
(b) Тело имеет равномерное ускорение, если оно движется прямолинейно и его скорость увеличивается на равные величины за равные промежутки времени. Например: Движение свободно падающего тела.

Вопрос 39:
Поезд едет первые 15 км с постоянной скоростью 30 км/ч; следующие 75 км с постоянной скоростью 50 км/ч; и последние 10 км с постоянной скоростью 20 км/ч. Вычислите среднюю скорость поезда на всем пути следования.
Решение:

Вопрос 40:
Поезд едет первые 15 км с постоянной скоростью 30 км/ч; следующие 75 км с постоянной скоростью 50 км/ч; и последние 10 км с постоянной скоростью 20 км/ч. Вычислите среднюю скорость поезда на всем пути следования.
Решение:

Вопрос 41:
Автомобиль движется по прямой дороге с постоянной скоростью. Он проходит 150 м за 5 секунд:
а) Какова его средняя скорость?
б) Какое расстояние он проходит за 1 секунду?
в) Какой путь он проходит за 6 секунд?
г) Сколько времени потребуется, чтобы пройти 240 м?
Решение:

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 22

Вопрос 55:
Тело движется по окружности радиуса R. Каковы будут пройденный путь и перемещение тела, когда оно совершит пол-оборота?
Решение:
Расстояние, пройденное за половину оборота по окружности, равно длине полукруга, т. е.

Вопрос 56:
Если в оба конца вы проедете 6 км и вернетесь домой:
(a) Какое расстояние вы преодолели?
(b) Каково ваше окончательное водоизмещение?
Решение:
(i) Пройденное расстояние = 6 км
(ii) Перемещение = ноль (поскольку конечное положение совпадает с начальным)

Вопрос 57:
Тело проходит расстояние 3 км на восток, затем 4 км на север и, наконец, 9 км на восток.
(i) Каково общее пройденное расстояние?
(ii) Каково результирующее смещение?
Решение:
(i) Общее пройденное расстояние = 3 + 4 +9 = 16 км
(ii) Тело проходит общее расстояние 12 км в восточном направлении, т. е. по оси x.
И он проходит расстояние 4 км в северном направлении, то есть по оси Y. Следовательно, результирующее смещение равно

Вопрос 58:
Мальчик идет из своего класса в книжный магазин по прямому коридору на север.Он преодолевает расстояние 20 м за 25 секунд, чтобы добраться до книжного магазина. Купив книгу, он преодолевает то же расстояние за то же время, чтобы вернуться в класс. Найдите (а) среднюю скорость и (б) среднюю скорость мальчика.
Решение:
(a) Общее расстояние, пройденное до книжного магазина и обратно в класс = 20 + 20 = 40 м
Общее время = 25 + 25 = 50 секунд

Вопрос 59:
Автомобиль проехал 100 км со скоростью 60 км/ч и вернулся со скоростью 40 км/ч.Вычислите среднюю скорость на всем пути.
Решение :
В первом случае автомобиль движется со скоростью 60 км/ч на расстояние 100 км
Во втором случае автомобиль движется со скоростью 40 км/ч на расстояние 100 км
Общее пройденное расстояние = 200 км

Вопрос 60:
Мяч ударяется о стену горизонтально на высоте 6,0 м с ^-1 . Он отскакивает горизонтально со скоростью 4,4 м с ^-1 . Мяч касается стены в течение 0.040 с. Чему равно ускорение мяча?
Решение:
Начальная скорость, u=6 м/с
Конечная скорость, v=-4,4 м/с (мяч отскакивает в противоположном направлении)
Время, t = 0,040 с Номер страницы: 39

Вопрос 1:
а) Что остается постоянным при равномерном круговом движении?
б) Что непрерывно изменяется при равномерном движении по окружности? ‘
Решение :
(а) Скорость
(б) Направление движения

Вопрос 2:
Укажите, верно или нет следующее утверждение:
Земля движется вокруг Солнца с постоянной скоростью.
Решение :
Нет, Земля движется вокруг Солнца с постоянной скоростью, но ее скорость постоянно меняется.

Вопрос 3:
Тело движется вокруг Солнца с постоянной скоростью по круговой орбите. Движение равномерное или ускоренное?
Решение :
Движение ускорено.

Вопрос 4:
Какой вывод вы можете сделать о скорости тела из приведенного ниже графика смещения во времени:

Решение:
Он представляет собой равномерную скорость.

Вопрос 5:
Назовите величину, которая измеряется площадью, занимаемой под графиком скорость-время.
Решение:
Расстояние, пройденное движущимся телом.

Вопрос 6:
На что указывает наклон графика зависимости скорости от времени?
Решение :
Наклон графика зависимости скорости от времени указывает на ускорение.

Вопрос 7:
На что указывает наклон графика зависимости расстояния от времени?
Решение :
Наклон графика зависимости расстояния от времени указывает скорость.

Вопрос 8:
Приведите пример движения, когда объект не меняет своей скорости, но его направление движения постоянно меняется.
Решение :
Движение Луны вокруг Земли.

Вопрос 9:
Назовите вид движения, при котором тело имеет постоянную, но не постоянную скорость.
Решение :
Равномерное круговое движение.

Вопрос 10:
Что можно сказать о движении тела, если его график зависимости скорости от времени представляет собой прямую линию, параллельную оси времени?
Решение :
Скорость тела постоянна или равномерна.

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 40

Вопрос 11:
Какой вывод о скорости тела вы можете сделать из следующего графика зависимости расстояния от времени?

Решение :
Тело имеет постоянную скорость.

Вопрос 12:
Что вы можете сказать о движении тела, график зависимости пути от времени которого представляет собой прямую линию, параллельную оси времени?
Решение :
Тело не движется. Он стационарный.

Вопрос 13:
Какой вывод об ускорении тела вы можете сделать из приведенного ниже графика зависимости скорости от времени?

Решение:
Представляет собой неравномерное ускорение.

Вопрос 14:
Спутник движется вокруг Земли по круговой орбите с постоянной скоростью. Движение равномерное или ускоренное?

Решение:
Это ускоренное движение, так как скорость постоянно меняется.

Вопрос 15:
Какое движение изображает кончик «секундной» стрелки часов? Он равномерный или ускоренный?
Решение:
Кончик «секундной» стрелки часов представляет собой равномерное круговое движение. Это ускоренное движение.

Вопрос 16:
Заполните следующие пропуски подходящими словами:
(а) Если тело движется с равномерной скоростью, его ускорение …………………………..
(б) Наклон график расстояние-время показывает…………………. . движущегося тела.
(c) Наклон графика скорость-время движущегося тела дает …………………………..
(d) На графике скорость-время площадь, ограниченная кривой скорость-время и ось времени дает…………….. телом.
(e) Возможно, что-то ускоряется, но не меняет своей скорости, если оно движется в…………………………..
Решение:
(a) ноль
(b) скорость
(c ) ускорение
(d) пройденное расстояние
(e) круговой путь

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 41

Вопрос 17:
Ускорено ли равномерное круговое движение? Обоснуйте свой ответ
Решение :
Да, равномерное круговое движение ускоряется, потому что скорость изменяется из-за непрерывного изменения направления движения.

Вопрос 18:
Напишите формулу для расчета скорости тела, движущегося по окружности. Укажите значение каждого символа, который в нем встречается.
Решение:
Скорость тела, движущегося по круговой траектории, определяется по формуле:
где v= скорость
=3,14 (постоянная величина)
r = радиус круговой траектории
t= время, затраченное на один круг по круговой траектории

Вопрос 19:
Объясните, почему движение тела, движущегося с постоянной скоростью по окружности, называется ускоренным.
Решение :
Движение тела, движущегося с постоянной скоростью по круговой траектории, называется ускоренным, потому что его скорость непрерывно изменяется из-за непрерывного изменения направления движения.

Вопрос 20:
В чем разница между равномерным линейным движением и равномерным круговым движением? Объясните примерами.
Решение:
Равномерное линейное движение — это равномерное движение вдоль линейного пути или прямой линии.Направление движения фиксировано. Значит не разгоняется. Например: автомобиль движется с постоянной скоростью 10 км/ч по прямой дороге.
Равномерное круговое движение — это равномерное движение по круговой траектории. Направление движения постоянно меняется. Значит, ускоряется. Например: движение Земли вокруг Солнца.

Вопрос 21:
Укажите важную характеристику равномерного кругового движения. Назовите силу, вызывающую равномерное круговое движение.
Решение :
Важной характеристикой равномерного кругового движения является то, что направление движения в нем непрерывно меняется со временем, поэтому оно ускоряется.
Центростремительная сила вызывает равномерное круговое движение.

Вопрос 22:
Найдите начальную скорость автомобиля, остановившегося за 10 секунд путем торможения. Запаздывание из-за тормозов составляет 2,5 м/с ² .
Решение:
Начальная скорость, u=?
Конечная скорость, v=0 м/с (автомобиль стоит)
Запаздывание, a=-2,5 м/с ²
Время, t=10 с
v=u + at
0=u +(-2,5)x 10
и=25 м/с

Вопрос 23:
Опишите движение тела с постоянным ускорением 10 м с ^– ² . Если тело выйдет из состояния покоя, какой путь оно пройдет за 2 с?
Решение:
Скорость этого тела увеличивается со скоростью «10 метров в секунду» каждую секунду.
Начальная скорость, u=0 м/с
Время, t=2 с
Ускорение, a=10 м/с ²

Вопрос 24:
Мотоцикл, движущийся со скоростью 5 м/с, подвергается ускорению 0,2 м/с ² . Определить скорость мотоцикла через 10 секунд и расстояние, пройденное за это время.
Решение:
Начальная скорость, u=5 м/с
Конечная скорость, v=?
Ускорение, a=0,2 м/с ²
Время, t=10 с
Используя , v=u + at
v=5 + 0,2 x 10
v=5 + 2 =7 м/с
Пройденное расстояние по времени рассчитывается;

Вопрос 25:
Автобус, движущийся со скоростью 18 км/ч, останавливается за 2,5 секунды путем торможения. Рассчитайте произведенное замедление.
Решение:
Начальная скорость, u=18 км/ч
Конечная скорость, v=0 м/с
Время, t=2. 5 сек
Ускорение, a=?
Используя , v= u + at

Таким образом, запаздывание равно 2 м/с ² .

Вопрос 26:
Поезд, тронувшийся с места, движется с равномерным ускорением 0,2 м/с ² в течение 5 минут. Вычислить полученную скорость и расстояние, пройденное за это время.
Решение:
Начальная скорость, u=0 м/с
Конечная скорость, v=?
Ускорение, a=0,2 м/с ²
Время, t=5 мин= 5 x60=300 с
Использование, v = u + at
v =0 + 0.2 x 300=60 м/с
Пройденное расстояние равно

Вопрос 27:
Назовите две величины, наклон графика которых дает:
(a) скорость и
(b) ускорение
Решение:
(a) Расстояние и время
(b) Скорость (или скорость) и время

Вопрос 28:
Гепард стартует, отдыхает и разгоняется до 2 м/с ² в течение 10 секунд. Рассчитайте:
(а) конечную скорость
(б) пройденное расстояние.
Решение:
Начальная скорость,
u=0 м/с
Конечная скорость, v=?
Ускорение, a = 2 м/с ²
Время, t = 10 с
(a) Использование,
v = u + at
v = 0 + 2 x 10 = 20 м/с
(b) Пройденное расстояние:

Вопрос 29:
Поезд, идущий со скоростью 20 м с ^-1, ускоряется со скоростью 0,5 м с ^-2 за 30 с. Какое расстояние он пройдет за это время?
Решение:
Начальная скорость, u=20 м/с
Время, t=30 с
Ускорение,
a=0.5 м/с ²
Пройденное расстояние:

Вопрос 30:
Велосипедист едет со скоростью 15 м с ^-1 . Она притормаживает, чтобы не столкнуться со стеной на расстоянии 18 м. Какое замедление она должна иметь?
Решение:
Начальная скорость, u=15 м/с
Конечная скорость, v=0 м/с
Расстояние, с=18 м
Ускорение, a=?
Значит, замедление равно 6,25 м/с ² .

Вопрос 31:
Нарисуйте график зависимости скорости от времени, чтобы показать следующее движение:
Автомобиль равномерно ускоряется из состояния покоя в течение 5 с; затем он движется с постоянной скоростью в течение 5 с.
Решение:

Вопрос 32:
График зависимости скорости от времени для части пути поезда представляет собой горизонтальную прямую линию. Что это говорит вам о
(а) скорости поезда и (б) о его ускорении?
Решение :
(a) Поезд имеет постоянную скорость.
(б) Ускорение отсутствует.

Вопрос 33:
(a) Объясните смысл следующего уравнения движения: v = u + at, где символы имеют свои обычные значения.
(б) Тело, выйдя из состояния покоя, движется с равноускоренным ускорением. Чему равно ускорение, если он пройдет 100 м за 5 с?
Решение :
(a) v=u + at — первое уравнение движения. { 2 }\), где символы имеют обычные значения.
(b) Поезд, тронувшийся с места и движущийся с равномерным ускорением, достигает скорости 36 км/ч за 10 минут. Найдите его ускорение.
Решение:
(a) Предположим, что тело имеет начальную скорость «u» и равномерное ускорение «a» в течение времени «t», так что его конечная скорость становится «v». Пусть путь, пройденный телом за это время, равен s. Путь, пройденный движущимся телом за время t, можно определить, рассматривая его среднюю скорость. Поскольку начальная скорость тела равна «u», а его конечная скорость равна «v», средняя скорость определяется по формуле:
(b) Начальная скорость, u=0 м/с
Конечная скорость, v=36 км/ч=10 м /с
Время, t=10мин =10 х 60=600 сек

Вопрос 36:
а) Напишите три уравнения равноускоренного движения.Укажите значение каждого символа, который в них встречается.
(б) Автомобиль достигает скорости 72 км/ч за 10 секунд, начиная с состояния покоя. Найдите
(i) ускорение,
(ii) среднюю скорость и
(iii) расстояние, пройденное за это время.
Решение:

Вопрос 37:
(а) Что понимается под равномерным круговым движением? Приведите два примера равномерного кругового движения.
(b) Кончику секундной стрелки дока требуется 60 секунд, чтобы пройти один раз по круглому циферблату часов.Если радиус циферблата часов равен 10,5 см, вычислите скорость кончика секундной стрелки часов. (Дано $\pi =\frac {22}{7}$).
Решение:
(a) Когда тело движется по окружности с постоянной скоростью (постоянной скоростью), его движение называется равномерным круговым движением. Например,
(i) Искусственные спутники совершают равномерное круговое движение вокруг Земли.
(ii) Движение велосипедиста по круговой дорожке.
(б) Скорость тела, движущегося по окружности, определяется формулой:
Дано, t=60 сек
Радиус, r=10.5 см=0,105 м

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 42

Вопрос 38:
Покажите графическим методом, что: v = u + at, где символы имеют свои обычные значения.
Решение :
Рассмотрим график зависимости скорости тела от времени, показанный на рисунке.
Тело имеет начальную скорость u в точке A, а затем его скорость равномерно изменяется от A до B за время t. Другими словами, существует равномерное ускорение a от A до B, и через время t его конечная скорость становится v, равной BC на графике.Время t представлено OC. Для завершения рисунка проведем перпендикуляр СВ из точки С, а AD проведем параллельно ОС. ВЕ перпендикуляр из точки В в ОЕ.
Теперь, Начальная скорость тела, u= OA —–(1)
И, Конечная скорость тела, v=BC ——(2)
Но из графика BC =BD + DC
Следовательно, v=BD + DC ——(3)
Снова DC = OA
Значит, v =BD + OA
Теперь из уравнения (1) OA =u
Итак, v=BD + u ——(4)
Надо выяснить стоимость BD сейчас. Мы знаем, что наклон графика зависимости скорости от времени равен ускорению a.{ 2 }\), где символы имеют свои обычные значения.
Решение :
Рассмотрим график зависимости скорости тела от времени, показанный на рисунке. Тело имеет начальную скорость u в точке A, а затем его скорость равномерно изменяется от A до B за время t. Другими словами, существует равномерное ускорение a от A до B, и через время t его конечная скорость становится v, равной BC на графике. Время t представлено OC.
Предположим, что тело проходит расстояние s за время t. На рисунке путь, пройденный телом, определяется площадью пространства между графиком скорость-время АВ и осью времени ОС, которая равна площади фигуры ОАВС.Таким образом:
Пройденное расстояние = Площадь фигуры OABC
= Площадь прямоугольника OADC + площадь треугольника ABD
Теперь найдем площадь прямоугольника OADC и площадь треугольника ABD.
(i) Площадь прямоугольника OADC = OA x OC
= uxt
= ut
(ii) Площадь треугольника ABD = _(1/2) x Площадь прямоугольника AEBD
= _(1/2) x AD x BD
= _(1/2) xtx при
= _(1/2) при ²
Пройденное расстояние, с = площадь прямоугольника OADC + площадь треугольника ABD

Вопрос 40:
Выведите графическим методом следующее уравнение движения: v ² = u ² + 2as, где символы имеют свои обычные значения.
Решение :
Рассмотрим график зависимости скорости тела от времени, показанный на рисунке. Тело имеет начальную скорость u в точке A, а затем его скорость равномерно изменяется от A до B за время t. Другими словами, существует равномерное ускорение a от A до B, и через время t его конечная скорость становится v, равной BC на графике. Время t представлено OC. Для завершения рисунка проведем перпендикуляр СВ из точки С, а AD проведем параллельно ОС. ВЕ перпендикуляр из точки В в ОЕ.
Путь s, пройденный телом за время t, определяется площадью фигуры OABC, которая представляет собой трапецию.
Пройденное расстояние, s = площадь трапеции OABC
Теперь, OA + CB = u + v и OC =t Подставляя эти значения в вышеприведенное соотношение, мы получаем:
Исключаем t из приведенного выше уравнения. Это можно сделать, получив значение t из первого уравнения движения.

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 43

Вопрос 53:
На приведенном рядом графике показано положение тела в разное время. Вычислите скорость тела, когда оно движется от:
(i) A до B,
(ii) B до C и
(iii) C до D.

Решение:
(i) от А до В равно(3-0) =3 см
Время, затрачиваемое на преодоление расстояния от А до В =(5-2) =3с
(ii) Скорость тела при движении из В в С равна нулю.
(iii) Расстояние от C до D равно (7-3)=4 см
Время, затрачиваемое на преодоление расстояния от C до D = (9-7)=2 с

Вопрос 54:
Что вы можете сказать о движении тела, если:
(a) его график смещения во времени представляет собой прямую линию?
(b) его график зависимости скорости от времени представляет собой прямую линию ?
Решение:
(a) Тело имеет постоянную скорость, если его график смещения во времени представляет собой прямую линию.
(b) Тело имеет равномерное ускорение, если его график зависимости скорости от времени представляет собой прямую линию.

Вопрос 55:
Тело с начальной скоростью x движется с равномерным ускорением y. Постройте его график зависимости скорости от времени.
Решение:

Вопрос 56:
Рядом приведен график зависимости скорости движущегося тела:
Найти:
(i) Скорость тела в точке C.
(ii) Ускорение, действующее на тело между A и
(iii ) Ускорение, действующее на тело между B и C.

Решение:
(i) BC представляет равномерную скорость. Из графика видно, что скорость тела в точке C = 40 км/ч
(ii) Ускорение между A и B = наклон линии AB
(iii) BC представляет равномерную скорость, поэтому ускорение, действующее на тело между B и С равен нулю.

Вопрос 57:
Тело движется прямолинейно равномерно со скоростью 5 м/с. Найдите графически путь, пройденный им за 5 секунд.
Решение:
Пройденное расстояние = Площадь прямоугольника OABC
= OA x OC
= 5 x 5 = 25 м

Вопрос 58:
Рядом приведен график зависимости скорости подъема пассажирского лифта от времени.
Чему равно ускорение лифта:
(i) в течение первых двух секунд?
(ii) между второй и десятой секундами ?
(iii) в течение последних двух секунд ?
Решение:

Вопрос 59:
Автомобиль движется по прямой дороге с равномерным ускорением. Скорость автомобиля зависит от времени следующим образом:
Время (ы): 0 2 4 6 8 10
Скорость (м / с): 4 8 12 16 20 24
Нарисуйте график скорости, выбрав удобный масштаб.Из этого графика:

(i) Рассчитайте ускорение автомобиля.
(ii) Рассчитайте расстояние, пройденное автомобилем за 10 секунд.
Решение:

Вопрос 60:
Приведенный рядом график показывает, как скорость автомобиля изменяется со временем:

(i) Какова начальная скорость автомобиля?
(ii) Какова максимальная скорость автомобиля?
(iii) Какая часть графика показывает нулевое ускорение?
(iv) Какая часть графика показывает разную задержку?
(v) Найдите расстояние, пройденное за первые 8 часов.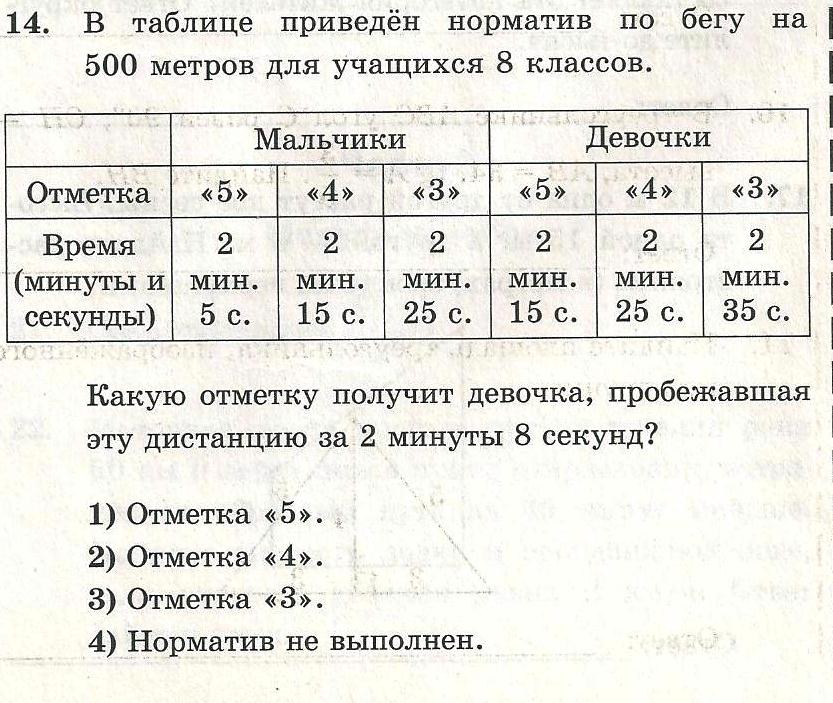
Решение:
(i) Начальная скорость автомобиля = 10 км/ч
(ii) Максимальная скорость, достигнутая автомобилем = 35 км/ч
(iii) BC представляет собой нулевое ускорение.
(iv) CD представляет различную задержку.
(в)

Вопрос 61:
Ниже приведены три графика зависимости скорости от времени:

Какой график представляет случай:
(i) мяч для крикета, брошенный вертикально вверх и возвращающийся в руки бросающего?
(ii) тележка, замедляющаяся до постоянной скорости, а затем равномерно ускоряющаяся?
Решение:
(i) График (c): Скорость мяча равномерно уменьшается по мере его движения вверх, достигает нуля в высшей точке, а затем равномерно увеличивается по мере его движения вниз.
(ii) Захват(а): Скорость тележки равномерно уменьшается, затем она движется с постоянной скоростью, а затем скорость равномерно увеличивается.

Лахмир Сингх Физика Класс 9 Решения Номер страницы: 44

Вопрос 62:
Изучите приведенный рядом график зависимости скорости автомобиля от времени и ответьте на следующие вопросы:

(i) Какой тип движения представлен ОА?
(ii) Какой тип движения представлен буквой AB?
(iii) Какой тип движения представлен BC ?
(iv) Каково ускорение автомобиля от О до А?
(v) Каково ускорение автомобиля из А в В?
(vi) Каково замедление автомобиля из В в С?
Решение:
(i) OA представляет равномерное ускорение
(ii) AB представляет постоянную скорость.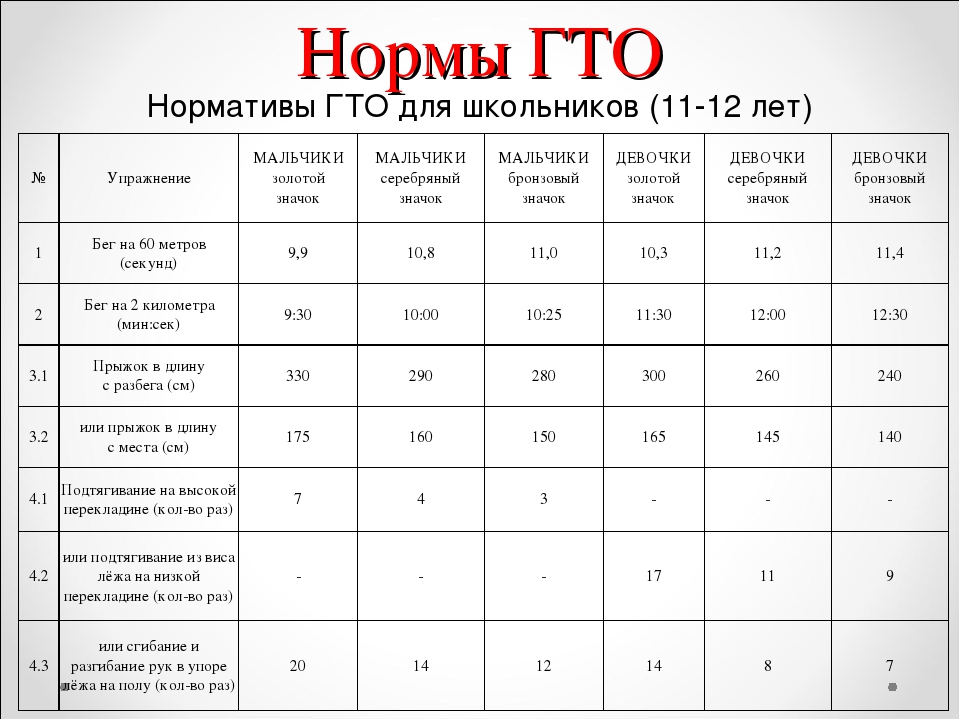
(iii) BC представляет равномерную задержку.
(iv) Ускорение автомобиля от O до A = наклон линии OA
(v) Ускорение автомобиля от A до B равно нулю, так как в это время он имеет постоянную скорость.
(vi) Замедление автомобиля из В в С = наклон линии ВС

Вопрос 63:
Какой тип движения представлен каждым из следующих графиков?

Решение:
(i) График (a) представляет равномерное ускорение.
(ii) График (b) представляет постоянную скорость.
(iii) График (c) представляет равномерное замедление.
(iv) График (d) представляет собой неравномерное замедление.

Вопрос 64:
Автомобиль едет по дороге в 8 мс ^-1 . Он разгоняется за 1 мс ^-2 на расстоянии 18 м. Как быстро он тогда движется?
Решение:
Начальная скорость, u=8м/с
Ускорение, a=1м/с ²
Расстояние, с=18м

Вопрос 65:
Автомобиль движется по дороге со скоростью 20 м/с. Ребенок выбегает на дорогу в 50 м впереди, и водитель автомобиля нажимает на педаль тормоза. Каким должно быть замедление автомобиля, если он должен остановиться прямо перед тем, как доедет до ребенка?
Решение:
Начальная скорость, u=20 м/с
Конечная скорость, v=0 м/с
Расстояние, s=50 м

Замедление автомобиля должно быть 4 м/с ² .

Энджел Джонсон из Viborg-Hurley устанавливает рекорд класса B в беге на 100 метров.

«Чтобы выйти и почти выиграть его на первом курсе, я был доволен собой, но я знал, что я действительно мог сделать», — сказал старший Viborg-Hurley.

Каждый последующий год ставил новые задачи. Во-первых, это была травма во время его кампании на втором курсе, которая помешала ему показать все свои лучшие качества на государственном мероприятии, где он занял третье место. А потом был отменен сезон из-за COVID для его младшего года.

У него осталась одна возможность доказать свою правоту.

И с 10.81, чтобы переписать свое имя в книге рекордов класса B, он доставил.

«Как раз вовремя. Я знал, что могу получить это, мне просто нужно было выйти и доказать. Это небольшое облегчение — выйти и получить это», — сказал Джонсон.

РЕЗУЛЬТАТЫ: Пятничная трасса штата встречается с

Джонсон победил Коллина Хельму из Freeman (11.06) и товарища по команде Чейза Мейсона (11.12) в пятничном забеге на 100 метров на стадионе О’Харра.

Viborg-Hurley может похвастаться огромной глубиной своей спринтерской группы, одержав победу в эстафете 4×200 (1:32.44) без Джонсона. Старший Эли Бумгарден заменил его, присоединившись к другим старшеклассникам Мэйсону и Картеру Гасту, а также второкурснику Джорджу Джонсону. В субботу у них также будет возможность принять участие в эстафетах 4×100 и 4×400 метров.

Мейсон также пробежал 100-метровую дистанцию, заняв третье место с результатом 11,12. Весь сезон он был ориентиром для Джонсона.

«Я знаю, что с Чейзом Мейсоном мы с ним ходим на каждую встречу, и мы всегда один-два в блоках. Если я смогу выйти и победить его, я знаю, что буду в хорошей форме, потому что он тоже один из самых быстрых», — сказал Джонсон.

Уайденер завершает сезон среди взрослых, завоевав титул в беге на 110 метров с барьерами Реле.
Ранее Уайденер был на самой большой сцене во время своего второго курса, когда он занял третье место, но волнение все еще было.
«Это был комок нервов, честно, я так нервничал.После той первой гонки я немного стеснялся. Ветер был очень сильным, подошел слишком близко к первому препятствию и чуть не сбил меня с ног», — сказал Уайденер.
Несмотря на небольшую неудачу в предварительных соревнованиях, в результате которой он стал вторым после Райана Бенсона из Честера, он преодолел это и выиграл финал с личным рекордом 14,61.
«Я вышел в последней гонке и сделал то, что у меня получается лучше всего, и просто преодолел препятствия», — сказал Уайденер. зеленый свет.
«У нас есть крытая трасса [в Лэнгфорде] всего с одной взлетно-посадочной полосой, и я провел на ней кучу времени, просто преодолевая препятствия и выходя из блоков, и действительно пытался улучшить свои навыки преодоления барьеров. Очевидно, это окупилось», — сказал он.
В следующем сезоне он продолжит бегать с барьерами на горе Марти.
Марли Гутмиллер из Ипсвича оглушает в прыжке с шестом
Семиклассница из Ипсвича Марли Гутмиллер не представляла себе, что превысит первую высоту 7-09 в пятничных соревнованиях, не говоря уже о том, чтобы побить свой предыдущий рекорд с 9-06, чтобы убежать с лучшая оценка в штате.
«Последний прыжок, я даже не подумал о том же. Я просто подумал: «О, давайте рассмотрим это, все в порядке», — сказал Гутмиллер.
Только начав прыжки с шестом в этом сезоне, Гатмиллер столкнулась с трудностями, соревнуясь со своими товарищами по команде. Ее подход к этому дню был простым, и это сделало работу для «Ипсвича».
«Я как раз думаю о том, чтобы сделать над ним сальто назад. Вот что я подумал, просто пройди его, носки до самого верха».
Гутмиллер превзошел результат товарища по команде Кейтлин Уильямс со счетом 9-03, поскольку эти двое вырвались из запланированной гонки с тремя участниками между лучшим старшим менно Морганом Эдельманом (J8-09), второкурсником из Сентервилля Бейли Хансеном (J8-03), и первокурсница Хендрикса Сэди Джонсон (J8-09).
101 лучший спринтер (100 метров) в легкой атлетике среди школьников Калифорнии — Новости спорта средней школы, результаты, видео, рейтинги
В этом сезоне они не будут участвовать в гонках, но это не значит, что они не заслуживают признания. Перечисленные ниже бегуны на 100 метров показали 101 лучшее время в штате Калифорния в прошлом сезоне и вошли в 2020 год, готовые побить рекорды.
Список отражает текущий год обучения спринтера в школе и дату, когда он пробежал указанное время в 2019 году.Пожалуйста, присылайте любые исправления или упущения по электронной почте [email protected].
ЛУЧШИЕ СПРИНТЕРЫ НА 100 МЕТРОВ В КАЛИФОРНИИ
№№ 101-97 — 11,05 сек
Майкл Джонсон – Пасифика (Окснард) – СР. – 25 апреля
Кейсон Джемениано – Роуленд – СР. – 4 мая 90 009 Адриан Романелло – Эльсинор – JR. – 4 мая
Кайл Уильямс – Хоторн (сейчас в Санта-Монике) – СР. – 10 апреля
№№ 96-93 — 11,04 секунды
Джейк Кнехт – Санта-Барбара – JR. – 4 мая
г. Джош Линг – Полуостров – СР. – 4 мая
Майлз МакАрн – Линкольн (Стоктон) – СР. – 14 марта
Тристан Хофманн – Марина – JR. – 3 апреля
№№ 92-90 — 11,03 секунды
Тай Янсон – Хеликс – Младший. – 27 апреля
Ник Терези – подготовка к колледжу Беллармин – SR. – 1 мая
Макари Уодли – Ванден – СР. – 26 апреля
№№ 89–85 — 11,02 секунды
Зайон Холл – Риджвью – JR. – 8 мая
Роберт Митчелл – Калифорния Сити – СР.– 29 марта
Мавин Андерсон – Миссия Вьехо – JR. – 16 марта
Джек Коваль – Чартер Оук – СР. – 25 апреля
Рейд Терри – Редвуд (Визалия) – JR. – 8 мая
№№ 84-81 — 11,01 сек
Джамаури Джексон – Мэдисон – JR. – 27 апреля
Эйс Джонс – Рамона – СР. – 11 мая
Джек Нортон – Карлмонт – СР. – 4 мая
г., Остин Паскуаль – Алисо Нигель – младший. – 26 апреля
№№ 80-79 — 11 секунд
Квентин Мотен – Ранчо Кукамонга – СР. – 23 апреля
Натан Грант – CA Rancho Cucamonga – JR. – 23 апреля
№№ 78-75 — 10,99 секунды
Мистер Дэвис – Альгамбра – СР. – 11 мая
Джастин Карагао – Санта-Маргарита – СР. – 28 марта, 90 009, Элайджа Бэнкс, Orange Vista, SR. – 8 апреля
г. Джейкоб Уильямс – Бреа Олинда – SR. – 23 апреля
№№ 74-73 — 10,98 сек
Джаксен Норт – Кимбалл – СР. – 2 мая
г. Доминик Бойкинс – Кахон – Младший. – 25 апреля
№72-69 — 10,97 секунды
Джамар Маршалл – Сент-Мэри – СР. – 11 апреля
Исайя Белл – Мемориал Гарсеса – СР. – 8 мая
Джеймс Харт – Вальехо – СР. — 16 апреля
Данте Джексон — Приятная долина — СР. – 10 мая
№ 68 — 10,96 секунды
Д’Мико Лейси — CA Rancho Cucamonga — SR. – 26 апреля
№№ 67-65 — 10,95 сек
Макс Томас – Сервит – ТАК. – 28 марта
Дэвид Гарсия – Нормандские острова – СР. – 15 марта
Девин Принс – Этиванда – Младший. – 23 апреля
№ 64 — 10,94 секунды
Кензел Лоулер – Рузвельт – СР. – 23 апреля
№№ 63-59 — 10,93 секунды
Джексон Моррелл — Экспресс-трек Revolution (Rocklin HS) — JR. – 7 июля
Франсиско Санчес – Менло-Атертон – СР. – 17 мая
Дариен Лэнгли – Сент-Джозеф (Санта-Мария) – JR. – 18 мая
Буба Фофунах – Кейт – СР. – 13 апреля
Дилан Итон – Джуниперо Серра – СР.– 13 апреля
№№ 58-57 — 10,92 секунды
Майки Холланд-младший – Мурпарк – младший. — 4 мая
года, Лиам Карр — Палм-Дезерт — СР. – 14 марта
№№ 56-54 — 10,91 секунды
Джейсон Уэйд – Антиохия – СР. – 4 мая 90 009 Эммануэль Джонс – Виста Мурриета – СР. – 25 апреля 90 009 Кристиан Рэндольф – Аделанто – Младший. – 30 марта
№№ 53-50 — 10,9 сек
Амари Дункан – Ривер-Сити – СР. – 26 апреля
Томас Уокер – Кеннеди (Сакраменто) – СР. – 3 мая
Эйден Липперт – Каньон Ла Коста – JR. — 18 апреля
Профет Браун — Монтерей Трейл — JR. – 20 апреля
№№ 49-47 — 10,89 сек
Фавор Ннаджи – Паттерсон – СР. – 1 мая
Кассиус Сэвидж – Вестерн – СР. – 22 апреля
Tylyn Cook – Валенсия (Валенсия) – SR. – 25 апреля
№№ 46-45 — 10,88 сек
Райан Серл – ул.Елена – SR. – 20 апреля 90 009 Брайс Лукас – Грейт-Оук – СР. – 25 апреля
№ 44 — 10,87 сек
Джейлен Нокс — Поликлиника Лонг-Бич — SO. – 18 апреля
№№ 43-41 — 10,86 сек
Мейсен Уильямс – Нарбонна – СР. – 17 мая,
, Девен Вандербильт – Вэлли Кристиан (Сан-Хосе) – СР. – 13 апреля
Джеймори Коннер – Лейзингер – Младший. – 4 мая
№№ 40-36 — 10,85 сек
Джален Дэвис – Золотая долина (Санта-Кларита) – JR. – 4 мая
Кристофер Бэнкс – Оранж Виста – Младший. – 4 мая
г. Делани Кроуфорд – Нагорье – SO. – 26 апреля, 90 009, Дэниел Сариски, Thousand Oaks, JR. – 11 апреля 90 009 Divine Peters – El Capitan – SR. – 9 мая
№№ 35-33 — 10,84 секунды
Эван Дэвидсон – Креспи – SO. – 17 апреля
Сейэр Райт – Лойола – JR. – 4 мая
г., Джон Крюгер – Ривер Вэлли – СР. – 26 апреля
№ 32 — 10,83 секунды
Карло Рейес – Лос Аламитос – JR.– 10 апреля
№№ 31-28 — 10,82 секунды
Эдвардс Вудс – Макклимондс – СР. – 24 апреля
Кристиан Траппс – EOTG (Окленд HS) – JR. – 7 июля
Ралик Браун – Эдисон – SO. – 2 мая
Питер Костелли – Миссия Вьехо – JR. – 4 мая
№№ 27-26 — 10,81 секунды
Кристиан Барнс – Бьюкенен – мл. – 25 апреля
Круа Стюарт – Американский каньон – SO. – 11 мая
№ 25 — 10.
8 секунд
Морган Даттон – Столетие Бейкерсфилда – SR. – 11 апреля
№№ 24-23 — 10,78 сек
Джалил Такер – Сент-Огастин – SO. – 11 мая 90 009 Марчелло Уотсон – Столетие Короны – SR. – 10 апреля
№№ 22-20 — 10,77 сек
Дэниел Феникс – Макклимондс – SR. – 16 мая
Исайя Смит – Линкольн (Сан-Диего) – СР. – 11 мая
Лоренцо Макмиллан – Кахон – СР. – 25 апреля
№19 — 10,76 секунды
Калеб Фостер – Кловис Норт – СР. – 30 марта
№ 18 — 10,75 сек
Ворота Николая – Калабасас – SO. – 4 мая
№№ 17-16 — 10,74 секунды
Тернер Фернандес – Вест (Торранс) – SR. 25 апреля 90 009 Ламон-Нарсисс – Калабасас – СР. 4 мая
№ 15 — 10,71 секунды
Патрик Дин – Колония – СР. – 4 мая
№14 — 10,7 секунды
Каден Рейнольдс – Алисо Нигель – СР. – 4 мая
№№ 13-11 — 10,69 секунды
Куртис Ли — Эвергрин-Вэлли — СР. – 16 марта
Патрик Изе-Ияму-младший – Chaminade – SO. – 04 мая
Энтони Джонсон – Лонг-Бич Поли – СР. – 18 апреля
№ 10 — 10,68 секунды
Хосе Делакруз – Хайленд – Младший. – 24 апреля
№9 — 10,67 сек
Джален Макмиллан – Мемориал Сан-Хоакина – СР.– 8 мая
№8 — 10,65 сек
Остин Кресли – Нортгейт – СР. – 11 мая
№7 — 10,63 секунды
Азжани Макгилл – MNVR Athletics (Monterey HS) – SR. – 9 июня
№№ 6-5 — 10,61 секунды
Исайя Марешо – Окснард – Младший. – 18 апреля
Сайлас Болден – Ранчо Кукамонга – СР. – 26 апреля
№4 — 10,59 сек
Рамон Хендерсон – Либерти (Бейкерсфилд) – СР.– 8 мая
№№ 3-2 — 10,55 секунд
Райшон Лука – Святой Иоанн Боско – С. О. — 24 мая
Ксавьер Уорти — Центральный — JR. – 8 мая

№ 1 — 10,48 секунды
Райан Малхолланд – Дель Оро – СР. — 24 мая

Нравится:
Нравится Загрузка. ..
Расстояние и смещение
Расстояние и смещение — две величины, которые могут казаться одним и тем же, но имеют совершенно разные определения и значения.
Расстояние — это скалярная величина, которая относится к тому, «сколько земли преодолел объект» во время своего движения.
Смещение — это векторная величина, которая указывает на то, «насколько далеко находится объект от места»; это общее изменение положения объекта.
Чтобы проверить свое понимание этого различия, рассмотрите движение, изображенное на диаграмме ниже.Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.
Несмотря на то, что учительница физики прошла в общей сложности 12 метров, ее перемещение равно 0 метрам. За время своего движения она «преодолела 12 метров земли» (расстояние = 12 м). Тем не менее, когда она заканчивает идти, она не находится «не на своем месте», т. Е. Для ее движения нет смещения (смещение = 0 м). Смещение, будучи векторной величиной, должно учитывать направление.4 метра на восток отменяет на 4 метра на запад; и 2 метра на юг отменяет 2 метра на север. Векторные величины, такие как смещение, учитывают направление . Скалярные величины, такие как расстояние, не знают направления. При определении общего расстояния, пройденного учителями физики, можно не учитывать различные направления движения.

Теперь рассмотрим другой пример. На приведенной ниже диаграмме показано положение лыжника в разное время.В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник движется из А в В, затем в С и в D.
С помощью диаграммы определите результирующее перемещение и расстояние, пройденное лыжником за эти три минуты. Затем нажмите кнопку, чтобы увидеть ответ.

В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время.В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, вагон перемещается из позиции A в B, затем в C и затем в D.
Каково результирующее перемещение и пройденное расстояние вагона? Нажмите кнопку, чтобы увидеть ответ.

Чтобы понять разницу между расстоянием и смещением, вы должны знать определения. Вы также должны знать, что векторная величина, такая как смещение, учитывает направление , а скалярная величина, такая как расстояние, не знает направления .Когда объект меняет направление движения, смещение учитывает это изменение направления; движение в противоположном направлении фактически начинает отменять любое смещение, которое когда-то было.
Извините! — Страница не найдена
Пока разбираемся, возможно, поможет одна из ссылок ниже.
Домой Назад
Класс
Онлайн-тесты
Ускоренный онлайн-курс JEE
Двухлетний курс ЕГЭ 2021
Класс
Онлайн-курс NEET
Серия онлайн-тестов
Фонд CA
CA Промежуточный
Финал CA
Программа CS
Класс
Серия испытаний
Книги и материалы
Испытательный зал
Интеллектуальный взломщик BBA
Обучение в классе
Онлайн-коучинг
Серия испытаний
Интеллектуальный взломщик IPM
Книги и материалы
ГД-ПИ
CBSE класс 8
CBSE класс 9
CBSE класс 10
CBSE Класс 11
CBSE Класс 12
Обучение в классе
Онлайн-классы CAT
Серия тестов CAT
MBA Жилой
Интеллектуальный взломщик CAT
Книги и материалы
Онлайн-классы без CAT
Серия испытаний без CAT
Испытательный зал
ГД-ПИ
Обучение в классе
Серия испытаний
Гражданские интервью
Класс
Онлайн-классы
Серия испытаний SSC
Переписка
Практические тесты
Электронные книги SSC
Пакет исследований SSC JE
Класс
RBI класс B
Серия тестов банка
Переписка
Электронные книги по банковскому делу
Банк ПДП
Онлайн-коучинг
Коучинг в классе
Серия испытаний
Книги и материалы
Класс
Программа моста GRE
Коучинг GMAT онлайн
Консультации по приему
Коучинг GMAT в классе
Стажировка
Корпоративные программы
Студенты колледжа
Работающие специалисты
Колледжи
Школы
Элейн Томпсон-Хера лидирует в ямайском забеге на 100 метров
ТОКИО —
Элейн Томпсон-Хера с Ямайки только что стала второй самой быстрой женщиной в истории.
Но ей понадобилось несколько секунд в субботу вечером на Играх в Токио, когда ее спросили, каково это — побить олимпийский рекорд в беге на 100 метров среди женщин.
— А-а, — начал Томпсон-Хера, — у меня болит горло.
Это была цена крика от радости в триумфе.
Томпсон-Хера несколько раз кричала после того, как пересекла финишную черту за 10,61 секунды и выиграла свою вторую подряд олимпийскую золотую медаль в главном соревновании.
Томпсон-Хера побила олимпийский рекорд — 10.62 секунды, которые были установлены Флоренс Гриффит Джойнер на Играх в Сеуле в 1988 году. Мировой рекорд Гриффита Джойнера 10,49 все еще в силе, но с учетом того, что шесть из восьми финалистов в субботу финишировали менее чем за 11 секунд, он, возможно, находится в пределах досягаемости, особенно для Томпсон-Хера.
«Всё возможно», — сказала она после проведения ямайской зачистки.
Шелли-Энн Фрейзер-Прайс выиграла серебряную медаль, а Шерика Джексон — бронзовую, так как ямайцы выиграли все медали впервые после Игр 2008 года в Пекине.
«Мы потрясающие», — сказал Томпсон-Хера.
Теана Дэниэлс, единственная американка в финале, сказала, что, хотя она хотела бы увидеть американский флаг во время церемонии награждения, ямайцы заслужили уважение за свои достижения.
«Прикольно их видеть, — сказал Дэниелс. — Они так много работали. … Я не могу злиться на талант и работу, которую они проделали».
Томпсон-Хера, которая также претендует на вторую подряд золотую медаль в беге на 200 метров, преодолела травму ахилла, из-за которой она замедлилась во время олимпийских испытаний на Ямайке в июне.Она заняла третье место в обоих соревнованиях.
«Два месяца назад — полтора месяца — я не думала, что окажусь здесь, — сказала она.
Томпсон-Хера в пятницу не проявила слабости, выиграв квалификационный заезд. Она также, казалось, блистала в полуфинале в субботу днем.
Ее самым большим соперником в финале стала Фрейзер-Прайс, четырехкратная олимпийская чемпионка, завоевавшая свою третью золотую медаль в беге на 100 метров. Мари-Жосс Та Лу из Кот-д’Ивуара также считалась главным претендентом.
Освещение Олимпийских игр в Токио
Но в субботу никто не смог поймать Томпсона-Хера.
«За этим 10.6 было много нервов», сказала она, «Ты можешь сделать это. Вы были здесь раньше. Просто выполните».
Фрейзер-Прайс сказала, что у нее были проблемы с третьим шагом после старта, и она так и не восстановилась.
«Как спортсменка я никогда не нахожу оправданий», — сказала она. «Вы просто должны появиться и выступить, несмотря ни на что».
В субботу отсутствовал один спринтер. Американка Ша’Карри Ричардсон, победительница соревнований на 100 метров на Олимпийских играх в США, была дисквалифицирована 30 июня после положительного результата теста на марихуану.
Томпсон-Хера спросили, как, по ее мнению, Ричардсон будет противостоять ей.
— Без комментариев, — сказала она.
Если Томпсон-Хера получит право на участие в Играх в Париже в 2024 году, у нее будет возможность сразиться с соотечественником Усэйном Болтом, который перед уходом из спорта трижды подряд выигрывал олимпийские золотые медали в беге на 100 м среди мужчин.
Томпсон-Хера сообщила, что у нее достаточно времени для большего успеха.
«Мне не 30, мне не 40», — сказала она. «Я все еще работаю.”
Незадолго до того, как был организован финал среди женщин на 100 метров, Соединенные Штаты, казалось, были готовы выиграть золотую медаль в первой смешанной эстафете на 1600 метров.
Но сборная США финишировала позади Польши и Доминиканской Республики и завоевала бронзу.
В пятницу вечером американская команда в составе Элайджи Годвина, Линны Ирби, Тейлора Мэнсона и Брайса Дэдмона объединилась для очевидной победы в своем заезде. Но официальные лица постановили, что первый проход между Годвином и Ирби был совершен за пределами обменной зоны, и У. Команда С. была дисквалифицирована. Затем команда США подала апелляцию.
Незадолго до часа ночи в субботу было объявлено, что команда США восстановлена и будет участвовать в финале.
Тревор Стюарт, Кендалл Эллис, Кейлин Уитни и Вернон Норвуд соревновались за США в субботу.
«Очень, очень волнительно быть частью истории и участвовать в таком веселом мероприятии, где мы собираемся показать лучшее, что есть в мужчинах и женщинах, и продемонстрировать всю глубину талантов, которыми мы обладаем с обеих сторон, — сказал Эллис.
Стюарт сказал: «Это определенно новый опыт, но только для книг».
Американцы Ронни Бейкер, Фред Керли и Трейвон Бромелл в воскресенье сойдутся в полуфинале и, возможно, финале на стометровке среди мужчин.
Бейкер выиграл квалификационный заезд в субботу за 10,03 секунды. Керли финишировал вторым в своем заезде за 9,97 секунды. Бромелл финишировал четвертым в своем заезде, но квалифицировался со временем 10,05 секунды.
.