Сколько доминошек: Правила игры Домино пластмассовое | Купить настольную игру в магазинах Мосигра

python — Сколько пар «дружных доминошек» можно составить из заданного набора доминошек

Вопрос задан 5 лет 1 месяц назад

Изменён 5 лет 1 месяц назад

Просмотрен 469 раз

Задача:

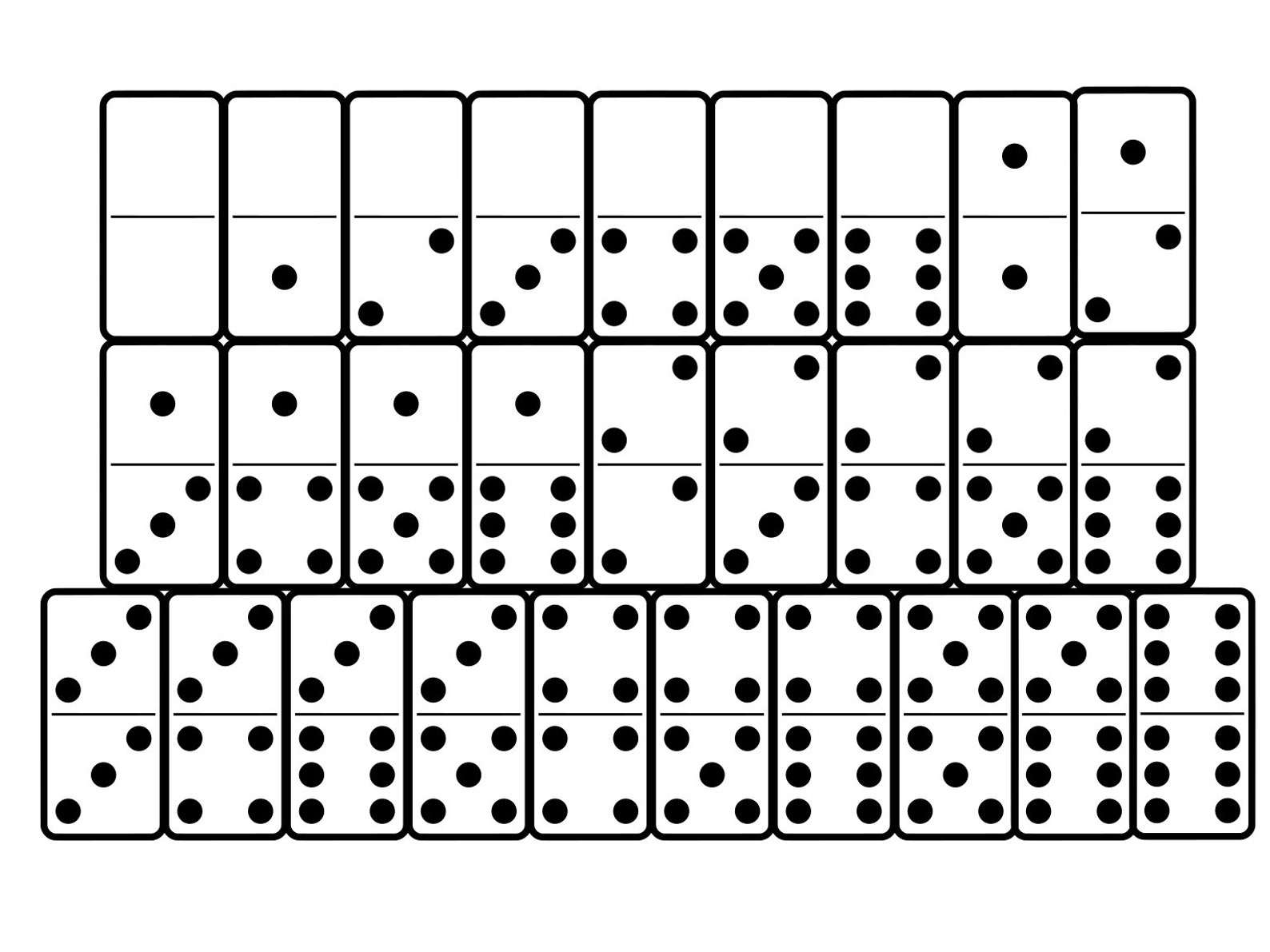
Вася нашел в комоде кучу доминошек из разных наборов. Каждая доминошка представляет собой прямоугольник, разделенный на две половинки. На каждой из половинок нарисовано от 0 до 6 точек. Ориентации доминошки не имеют — их можно как угодно поворачивать.

Вася решил называть «дружными доминошками» пару доминошек, которые можно поставить в игре рядом (то есть доминошки в паре соприкасаются половинками с равными числами) в том или ином порядке.

По заданному набору доминошек определите, сколько пар «дружных доминошек» можно составить из него. Пары, отличающиеся хотя бы одной доминошкой, считаются различными. По-разному составленная пара из одних и тех же доминошек считается один раз.

Примеры:

Пример 1 Ввод:

2
1 2
2 3

Вывод:

1

Пример 2 Ввод:

5
1 2
2 3
3 1
4 3
4 3

Вывод:

8

Я сделал рабочий скрипт, но он не зашёл в чекер, слишком долго работает. Нужно через словари решить как-то. Подскажите, примерно как

• python
• алгоритм
• python-3.x

2

Разных костяшек всего 28. Заводим треугольную таблицу, заполняем нулями.

Добавляем домино по одной штуке.

Для кости a|b, где a<=b добавляем к результату сумму строки а, сумму столбца b, и отнимаем значение ячейки a|b
(последнее нужно для отработки условия По-разному составленная пара из одних и тех же доминошек считается один раз)

Инкрементируем ячейку a|b и суммы строки а и столбца b

1

Метод грубой силы: O(M + N**3) алгоритм, где M — количество домино на входе, а N=7 для примера с домино:

• если на входе n костяшек домино с a точек на одной половинке и b точек на другой (a:b костяшка), то записываем n в (a, b) и (b, a) элементы NxN матрицы

• обходим все возможные костяшки i:j такие что i <= j («ориентации доминошки не имеют»)

  • если больше одной i:j костяшки (дубликаты), то C(n, 2) уникальных пар получается (количество способов выбрать два предмета из n набора), где n— количество дубликатов (количество i:j костяшек)
  • каждые m домино k:j ниже в том же столбце образуют n x m пар с текущими i:j домино (n костяшек на первом месте, m костяшек на втором месте пары). Местами не меняются, так как «По-разному составленная пара из одних и тех же доминошек считается один раз»
  • аналогично для строки: каждые m домино i:k справа в той же строке образуют n x m пар. Для диагональных домино (i:i — одинаковые половинки), так как нет разницы при вращении костяшек, то проход по строке пропускается, чтобы дважды не считать одинаковые пары (i:i i:k и i:i k:i).

#!/usr/bin/env python
# read dominoes
N = 7
dominoes = [[0] * N for _ in range(N)]
for _ in range(int(input())):
    i, j = map(int, input().split())
    dominoes[j][i] = dominoes[i][j] = dominoes[i][j] + 1
# count "friendly" pairs
npairs = 0
for i in range(N):  # for each domino i:j where i <= j
    for j in range(i, N):
        n = dominoes[i][j]
        if n:
            npairs += n * (n - 1) // 2   # {n \choose 2} pairs with itself
            for k in range(i+1, N):      # top-down
                npairs += dominoes[k][j] * n
            if i != j:  # don't count twice 
                for k in range(j+1, N):      # left-right
                    npairs += dominoes[i][k] * n
print(npairs)

Пример.

2

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

By clicking “Отправить ответ”, you agree to our terms of service and acknowledge that you have read and understand our privacy policy and code of conduct.

Замощение доминошками / Хабр

Одна из первых действительно интересных задач по математике, с которыми я столкнулся формулируется так: «из шахматной доски вырезали две противоположные по диагонали угловые клетки, можно ли оставшуюся часть разрезать на «доминошки» — фигурки из двух клеток, у которых одна сторона общая?». У нее очень простая формулировка, в отличие от великой теоремы Ферма она имет простое, элегантное, но неочевидное решение (если вы знаете решение задачи, то попробуйте применить его к фигуре справа).

В этой статья я расскажу о нескольких алгоритмах, которые умеют покрывать доминошками произвольную клетчатую фигуру на плоскости, если это возможно, находить ситуации, когда это невозможно и считать количество возможных замощений доминошками.

Nota bene! Материал этой статьи — это усеченный вариант вот этого jupyter-notebook, все картинки и анимации, которые вы увидите в статье, сгенерированы кодом из этого ноутбука (правда анимаций не будет в github предпросмотре). К слову, картинки из заголовка также сгенерированы с помощью python/matplotlib

Вспомогательный код для отрисовки, он еще пригодится

import matplotlib.pyplot as plt
from matplotlib import colors as mcolors
colors = dict(mcolors.BASE_COLORS, **mcolors.CSS4_COLORS)
# Sort colors by hue, saturation, value and name. 
by_hsv = sorted((tuple(mcolors.rgb_to_hsv(mcolors.to_rgba(color)[:3])), name)
                for name, color in colors.items())
names = [name for hsv, name in by_hsv if name not in {'black', 'k', 'w', 'white', 'crimson', 'royalblue', 'limegreen', 'yellow', 'orange'}]
import random
random.shuffle(names)
names = ['crimson', 'royalblue', 'limegreen', 'yellow', 'orange', *names]
names.append('red')
names.append('white')
names.append('black')

def fill_cell(i, j, color, ax):
    ax.fill([i, i, i + 1, i + 1, i], [j, j + 1, j + 1, j, j], color=color)
def draw_filling(filling):
    if filling is not None:
        n = len(filling)
        m = len(filling[0])
        fig = plt.figure(figsize=(m * 0.75, n * 0.75))
        ax = fig.add_axes([0, 0, 1, 1])
        ax.get_xaxis().set_visible(False)
        ax.get_yaxis().set_visible(False)      
        for name, spine in ax.spines.items():
            spine.set_visible(False)
            spine.set_visible(False)
        for i, row in enumerate(filling):
            i = n - i - 1
            for j, cell in enumerate(row):
                fill_cell(j, i, names[cell], ax)
        for i in range(n + 1):
            ax.
  plot([0, m], [i, i], color='black')
        for i in range(m + 1):
            ax.plot([i, i], [0, n], color='black')
        plt.close(fig)
        return fig
    else:
        return None

Прежде, чем перейти дальше, решение исходной задачи

Сделать это невозможно, и этому есть красивое и простое объяснение:

• На оставшейся части доски 30 черных и 32 белых клетки
• Каждая доминошка состоит из одной черной и одной белой клетки
• Как бы мы не разрезали фигуру на доминошки, в итоге на доминошках будет равное число белых и черных клеток

Динамическое программирование по профилю

Про динамического программирования есть статья на хабре, которая даже содержит пример с покрытием доминошками, я немного расширю этот пример.

Основная суть динамического программирования заключается в том, чтобы придумать для исходной задачи какие-то промежуточные подзадачи так, чтобы их можно было легко друг через друга выразить. Например, если мы хотим вычислить двухсотое число Фибоначчи, то для этого можно последовательно вычислить все числа Фибоначчи вплоть до нужного нам применяя соотношение

Аналогично можно вычислить число «сочетаний» , воспользовавшись одним из следующих рекуррентных соотношений

Для задачи «можно ли замостить доминошками прямоугольник ?» к сожалению подобных простых соотношений не существует. Тем не менее, если мы рассмотрим более широкий класс фигурок, то такие соотношения уже станут возможными, главное чтобы это не были слишком маленькие классы и динамическое программирование не превратилось в банальный перебор.

Посмотрим на следующий класс фигурок: у нас есть прямоугольник , на строке присутствуют первые клеток, остальные задаются

профилем, на строке первые клеток задаются профилем, остальные не участвуют. Профиль — это последовательность нулей и единичек длины : если на -ой позиции профиля единичка, это значит что в этой фигуре есть соответствующая клетка, всего профилей (красные клетки — единички, синие — нули).

Профиль однозначно задается числом (его бинарное представление вплоть до разрядов является последовательностей нулей и единичек).

Прямоугольник соответствует фигуре с , и нулевым профилем. На фигурках такого типа мы можем считать две основные функции

• Максимальное возможное число покрытых доминошками клеток в этой фигуре
• Количество способов полностью покрыть доминошками эту фигуру

Давайте обозначим за количество способов замостить такую фигурку, тогда и при этом выражается через сумму нескольких , по большому счету переход от к — это перебор трех случаев: поставить вертикальную доминошку, если это возможно

горизонтальную доминошку, если это возможно

и пропустить занятую клетку. В случае, если мы пытаемся понять, какое максимальное число клеток фигурки возможно замостить, то сумма заменяется на максимум и добавляется один несложный переход — пропуск свободной клетки. Важным моментом также является то, что мы можем заранее вырезать несколько клеток, принципиально от этого ничего не поменяется.

Давайте теперь попробуем реализовать это (кода будет много, так что большинство я вынесу в спойлер). Зададим интересующий нас прямоугольник как множество строк из точек и решеток (точка — свободная клетка, решетка — занятая), пока все клетки будут свободными, потом потихоньку будем какие-нибудь вырезать

tiling = [
    '........',
    '........',
    '........',
    '........',
    '........',
    '........',
    '........',
    '........',
]

Начнем с

количества способов замощений доминошками

def count_tilings(tiling):
    n = len(tiling)
    m = len(tiling[0])
    if ((n + 1) * m * 2 ** m) <= 10000000:
        dp = [[[(0 if k != 0 or j != 0 or mask != 0 else 1) for mask in range(2 ** m)] for j in range(m)] for k in range(n + 1)]
    for k in range(n):
        for j in range(m):
            for mask in range(2 ** m):
                # Вертикальная доминошка
                if k < n - 1 and tiling[k][j] == '.' and tiling[k + 1][j] == '. ' and (mask &  (1 << j)) == 0:
                    dp[k + ((j + 1) // m)][(j + 1) % m][mask + (1 << j)] += dp[k][j][mask]
                # Горизонтальная доминошка
                if j < m - 1 and tiling[k][j] == '.' and tiling[k][j + 1] == '.' and (mask & (3 << j)) == 0:
                    dp[k + ((j + 1) // m)][(j + 1) % m][mask + (2 << j)] += dp[k][j][mask]
                # Клетка занята
                if ((1 << j) &  mask) != 0 or tiling[k][j] != '.':
                    dp[k + ((j + 1) // m)][(j + 1) % m][(mask | (1 << j)) - (1 << j)] += dp[k][j][mask]
    return dp

dp = count_tilings(tiling)
print(dp[8][0][0])

получаем

12988816

Сверяемся с википедией, пока все в порядке. Давайте еще на всякий случай проверим, количество способов замостить полоску — должно получиться число Фибоначчи.

tiling_fib = [
    '..',
    '..',
    '..',
    '..',
    '..',
    '..',
    '..',
    '..'
]
dp = count_tilings(tiling_fib)
for i in range(8):
    print(dp[i][0][0], end=' ')

1 1 2 3 5 8 13 21

Что ж, поехали дальше, проверим на доске с вырезанными углами

tiling_no_corners_opposite = [
    '. ......#',
    '........',
    '........',
    '........',
    '........',
    '........',
    '........',
    '#.......',
]
dp = count_tilings(tiling_no_corners_opposite)
print(dp[8][0][0])

0

Супер. Допустим вычислять количество мы научились, может найдем хотя бы одно конкретное замощение для наглядности?

код для получения покрытия

def cover_if_possible(tiling, dp=None):
    if dp is None:
        dp = count_tilings(tiling)
    n = len(dp) - 1
    m = len(dp[0])
    if dp[n][0][0] == 0:
        return None
    result = [[-1 if tiling[i][j] == '#' else 0 for j in range(m)] for i in range(n)]
    num = 0
    k = n
    j = 0
    mask = 0
    while k > 0 or j > 0:
        #print(k, j, mask)
        prev_j = j - 1
        prev_k = k
        if prev_j == -1:
            prev_j += m
            prev_k -= 1
        # Начинаем перебирать варианты, каким образом мы могли попасть в i, j, mask
        # Этот вариант очень не оптимален, но занимает меньше кода и все равно быстрее 
        # самого подсчета динамики
        for prev_mask in range(2 ** m):
            if prev_k < n - 1 and tiling[prev_k][prev_j] == '. ' and tiling[prev_k + 1][prev_j] == '.' and \
                (prev_mask & (1 << prev_j)) == 0 and (prev_mask + (1 << prev_j)) == mask and dp[prev_k][prev_j][prev_mask] != 0:
                mask = prev_mask
                result[prev_k][prev_j] = num
                result[prev_k + 1][prev_j] = num
                #print(f'Vertical at ({prev_k}, {prev_j}) ({prev_k + 1}, {prev_j})')
                num += 1
                break
            elif prev_j < m - 1 and tiling[prev_k][prev_j] == '.' and tiling[prev_k][prev_j + 1] == '.' and (prev_mask & (3 << prev_j)) == 0 and \
                prev_mask + (2 << prev_j) == mask and dp[prev_k][prev_j][prev_mask] != 0:
                mask = prev_mask
                result[prev_k][prev_j] = num
                result[prev_k][prev_j + 1] = num
                #print(f'Horisontal at ({prev_k}, {prev_j}) ({prev_k}, {prev_j + 1})')
                num += 1
                break
            elif (((1 << prev_j) & prev_mask) != 0 or tiling[prev_k][prev_j] != '. ') and \
                (prev_mask | (1 << prev_j)) - (1 << prev_j) == mask and dp[prev_k][prev_j][prev_mask] != 0:
                mask = prev_mask
                break
        j = prev_j
        k = prev_k
    return result

filling = cover_if_possible(tiling)
draw_filling(filling)

Слишком просто, давайте вырежем несколько клеток

tiling_random = [
    '........',
    '#.#.....',
    '..#.....',
    '........',
    '........',
    '........',
    '........',
    '...#....'
]
filling_random = cover_if_possible(tiling_random)
draw_filling(filling_random)

Попробуем теперь сделать тоже самое для замощения максимальной возможной части фигуры

Код для максимального замощения

def maxmimum_cover(tiling):
    n = len(tiling)
    m = len(tiling[0])
    if ((n + 1) * m * 2 ** m) <= 10000000:
        dp = [[[(n * m if k != 0 or j != 0 or mask != 0 else 0) for mask in range(2 ** m)] for j in range(m)] for k in range(n + 1)]
    for k in range(n):
        for j in range(m):
            for mask in range(2 ** m):
                next_k, next_j = k + ((j + 1) // m), (j + 1) % m
                # Вертикальная доминошка
                if k < n - 1 and tiling[k][j] == '. ' and tiling[k + 1][j] == '.' and (mask &  (1 << j)) == 0:
                    dp[next_k][next_j][mask + (1 << j)] = min(dp[next_k][next_j][mask + (1 << j)], dp[k][j][mask])
                # Горизонтальная доминошка
                if j < m - 1 and tiling[k][j] == '.' and tiling[k][j + 1] == '.' and (mask & (3 << j)) == 0:
                    dp[next_k][next_j][mask + (2 << j)] = min(dp[next_k][next_j][mask + (2 << j)], dp[k][j][mask])
                # Клетка занята
                if ((1 << j) &  mask) != 0 or tiling[k][j] != '.':
                    dp[next_k][next_j][(mask | (1 << j)) - (1 << j)] = \
                        min(dp[next_k][next_j][(mask | (1 << j)) - (1 << j)], dp[k][j][mask])
                # Клетка не занята, рассмотриваем случай её пропуска
                else:
                    dp[next_k][next_j][(mask | (1 << j)) - (1 << j)] = \
                        min(dp[next_k][next_j][(mask | (1 << j)) - (1 << j)], dp[k][j][mask] + 1)
    return dp
def cover_maximum_possible(tiling, dp=None):
    if dp is None:
        dp = maxmimum_cover(tiling)
    n = len(dp) - 1
    m = len(dp[0])
    result = [[-1 if tiling[i][j] == '#' else -2 for j in range(m)] for i in range(n)]
    num = 0
    k = n
    j = 0
    mask = 0
    while k > 0 or j > 0:
        #print(k, j, mask)
        prev_j = j - 1
        prev_k = k
        if prev_j == -1:
            prev_j += m
            prev_k -= 1
        # Начинаем перебирать варианты, каким образом мы могли попасть в i, j, mask
        # Этот вариант очень не оптимален, но занимает меньше кода и все равно быстрее 
        # самого подсчета динамики
        for prev_mask in range(2 ** m):
            # Раньше мы здесь проверяли, что количество вариантов в этой ветке не 0, сейчас нужно
            # проверить, что эта ветка ведет к максимальному покрытию
            if prev_k < n - 1 and tiling[prev_k][prev_j] == '. ' and tiling[prev_k + 1][prev_j] == '.' and \
                    (prev_mask & (1 << prev_j)) == 0 and (prev_mask + (1 << prev_j)) == mask and \
                    dp[prev_k][prev_j][prev_mask] == dp[k][j][mask]:
                mask = prev_mask
                result[prev_k][prev_j] = num
                result[prev_k + 1][prev_j] = num
                num += 1
                break
            elif prev_j < m - 1 and tiling[prev_k][prev_j] == '.' and tiling[prev_k][prev_j + 1] == '.' and (prev_mask & (3 << prev_j)) == 0 and \
                    prev_mask + (2 << prev_j) == mask and dp[prev_k][prev_j][prev_mask] == dp[k][j][mask]:
                mask = prev_mask
                result[prev_k][prev_j] = num
                result[prev_k][prev_j + 1] = num
                num += 1
                break
            elif (((1 << prev_j) & prev_mask) != 0 or tiling[prev_k][prev_j] != '.') and \
                    (prev_mask | (1 << prev_j)) - (1 << prev_j) == mask and dp[prev_k][prev_j][prev_mask] == dp[k][j][mask]:
                mask = prev_mask
                break
            elif ((1 << prev_j) & prev_mask) == 0 and tiling[prev_k][prev_j] == '. ' and \
                    (prev_mask | (1 << prev_j)) - (1 << prev_j) == mask and dp[prev_k][prev_j][prev_mask] + 1 == dp[k][j][mask]:
                mask = prev_mask
                break
        j = prev_j
        k = prev_k
    return result

И попробуем фигурку из заголовка

tiling_custom=[
    '...####',
    '....###',
    '......#',
    '#.#....',
    '#......',
    '##.....',
    '###...#',
]
filling = cover_maximum_possible(tiling_custom)
draw_filling(filling)

Опа! Не получилось, в общем так и должно было быть. Прежде, чем пойти дальше пару слов о сложности алгоритмов. Всего фигурок , все переходы константные, отсюда асимптотика , которая может быть улучшена до если добавить транспонирование в случае, если . Построение конкретного замощения в приведенных реализациях имеет сложность , но можно сделать так, чтобы было просто , но это банально больше кода.

Замощение с помощью решения задачи о максимальном паросочетании

Возвращаясь к черно-белой раскраске как на шахматной доске можно заметить интересную интерпретацию задачи замощения доминошками.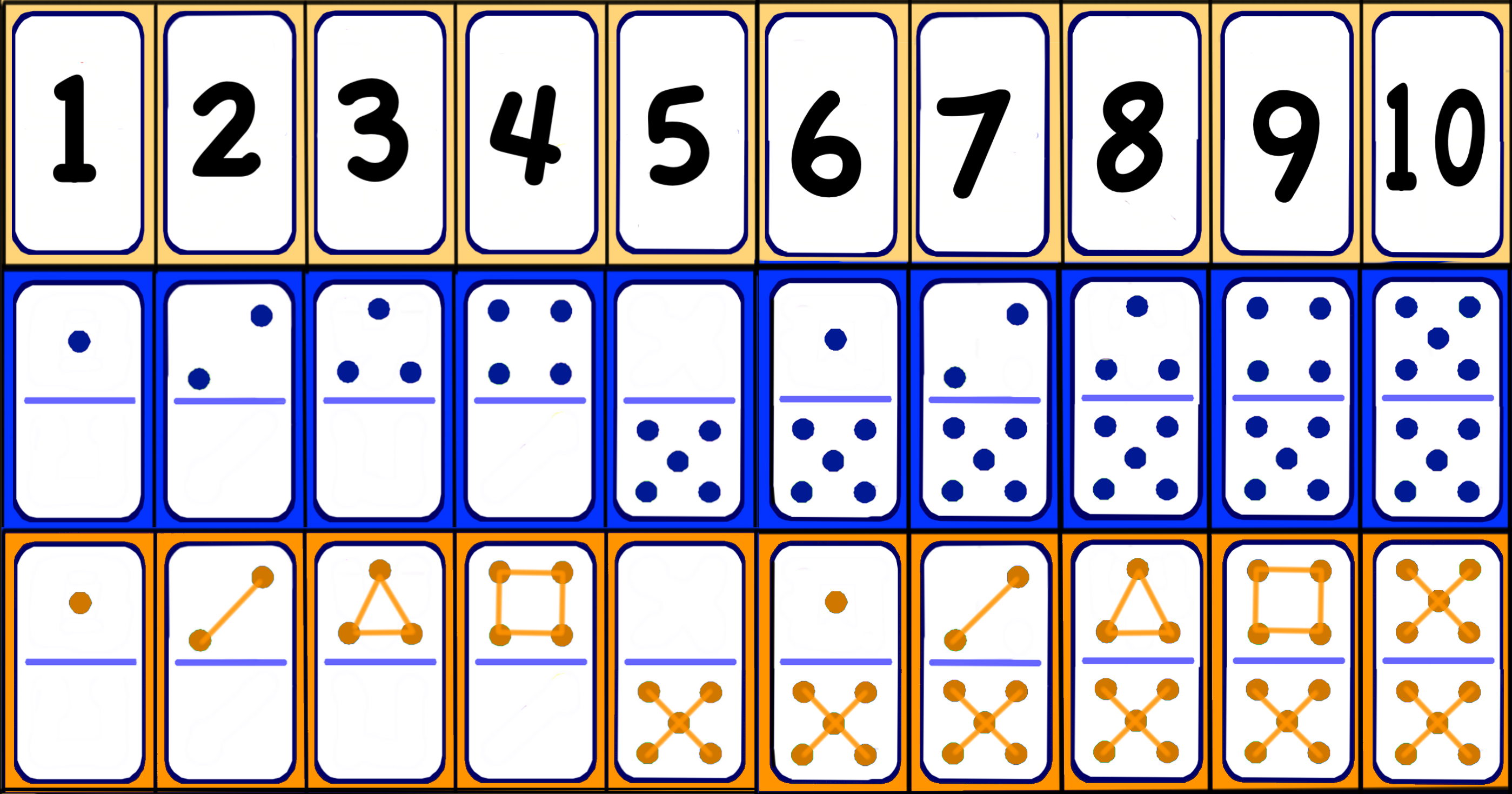 Давайте посмотрим на граф, в котором клетки фигуры — это вершины, ребрами соединены клетки, имеющие общую сторону. Так вот, доминошка в этом графе — это как раз ребро. Если раскрасить граф в шахматном порядке, то внезапно можно обнаружить, что этот граф — двудольный, черные — одна доля, белые — другая. Если переформулировать задачу замощения наибольшего числа клеток в терминах этого графа, то получается, что нужно найти максимальное по размеру множество ребер такое, чтобы вершины являлись концом не более одного ребра. В общем то, это довольно известная задача о максимальном паросочетании. Давайте попробуем её применить для решения этой задачи, тут получится даже с анимацией, приведу базовый алгоритм Куна для нахождения максимального паросочетания.

Реализация алгоритма Куна для паросочетаний на графе доминошек

def check_valid(i, j, n, m, tiling):
    return 0 <= i and i < n and 0 <= j and j < m and tiling[i][j] != '#'
def find_augmenting_path(x, y, n, m, visited, matched, tiling):
    if not check_valid(x, y, n, m, tiling):
        return False
    if (x, y) in visited:
        return False
    visited. add((x, y))
    for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
        if not check_valid(x + dx, y + dy, n, m, tiling):
            continue
        if (x + dx, y + dy) not in matched or find_augmenting_path(*matched[(x + dx , y + dy)], n, m, visited, matched, tiling):
            matched[(x + dx, y + dy)] = (x, y)
            return True
    return False
def convert_match(matched, tiling, n, m):
    result = [[-1 if tiling[i][j] == '#' else -2 for j in range(m)] for i in range(n)]
    num = 0
    for x, y in matched:
        _x, _y = matched[(x, y)]
        result[x][y] = num
        result[_x][_y] = num
        num += 1
    return result
def match_with_flow(tiling):
    result_slices = []
    n = len(tiling)
    m = len(tiling[0])
    matched = dict()
    # Для наглядности визуализации
    rows = list(range(n))
    columns = list(range(m))
    random.shuffle(rows)
    random.shuffle(columns)
    result_slices.append(convert_match(matched, tiling, n, m))
    for i in rows:
        for j in columns:
            if (i + j) % 2 == 1:
                continue
            visited = set()
            if find_augmenting_path(i, j, n, m, visited, matched, tiling):
                result_slices. append(convert_match(matched, tiling, n, m))
    return result_slices

Здесь даже получается проанимировать процесс

sequencial_match = match_with_flow(tiling_custom)

Суть алгоритма Куна (да и любого другого алгоритм для нахождения максимального паросочетания) заключается в нахождении «аугментирующих путей». В терминах доминошек это цепочка из доминошек, у которой рядом с доминошками на концах есть по свободной клетке, такие цепочки можно заменить на цепочки большей длины, охватывающие те же клетки и заполняя две свободные клетки рядом с концами цепочки. Более того, основное утверждение, на котором работают все алгоритмы нахождения максимального паросочетания, заключается в том, что если такой цепочки не удается найти, то значит большего замощения нам не получить.

UPD. Для последнего примера простое обоснование на основе черно-белой раскраски не работает. Насколько мне известно, есть два общих критерия для существования полного замощения:

• Теорема Холла (теорема о свадьбах)
  Проверка условий этой теоремы вычислительно сложнее, чем построить максимальное паросочетание.
• Условие высоты Тёрстона про это я мало что знаю

Недавно меня навели на очень интересную статью про замощения, там в том числе описывается про использовании групп для доказательства невозможности различных замощений.

Бонус! Раскраска планарного графа в 5 цветов.

Для визуализации замощения я использовал отдельный цвет для каждой доминошки. К сожалению некоторые цвета не очень хорошо смотрятся, а некоторые плохо контрастируют друг с другом. В этом случае подобрать цвета для хорошего контраста не так уж просто, особенно если доминошек много. Зато можно использовать меньше цветов: доминошки, которые не находятся рядом друг с другом можно раскрасить в одинаковый цвет, тогда визуально все еще будет понятно, как именно выглядит покрытие. В общем то это классическая задача о раскраске вершин планарного графа. Любой планарный граф можно покрасить в 4 цвета, правда хорошего алгоритма для такой покраски нет. Зато есть довольно простой алгоритм для покраски в 5 цветов, когда правда все еще много, и я его мало тестировал (если необходим 5ый цвет, то возможны баги)

Покраска доминошек в 5 цветов

def color_5(filling):
    result = [[i for i in row] for row in filling]
    # Строим граф
    domino_tiles = [[] for i in range(max(map(max, filling)) + 1)]
    domino_neighbours = [set() for i in range(max(map(max, filling)) + 1)]
    degree = [0 for i in range(max(map(max, filling)) + 1)]
    n = len(filling)
    m = len(filling[0])
    for i, row in enumerate(filling):
        for j, num in enumerate(row):
            if num >= 0:
                domino_tiles[num]. append((i, j))
    for i, tiles in enumerate(domino_tiles):
        for x, y in tiles:
            for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1), (-1, -1), (-1, 1), (1, -1), (1, 1)]:
                a, b = x + dx, y + dy
                if 0 <= a and a < n and 0 <= b and b < m and filling[a][b] >= 0 and filling[a][b] != i \
                        and filling[a][b] not in domino_neighbours[i]:
                    domino_neighbours[i].add(filling[a][b])
                    degree[i] += 1
    # Первым делом нужно найти такой порядок вершин, все вершины имели не больше 5 соседей среди
    # предыдущих. Такой существует в силу того, что граф планарный, а найти его эффективнее всего
    # по очереди находя вершину наименьшей степени и удаляя её из графа, так мы получаем обратный порядок
    active_degrees = [set() for i in range(max(degree) + 1)]
    for i, deg in enumerate(degree):
        active_degrees[deg].add(i)
    reversed_order = []
    for step in range(len(domino_tiles)):
        min_degree = min([i for i, dominoes in enumerate(active_degrees) if len(dominoes) > 0])
        domino = active_degrees[min_degree]. pop()
        reversed_order.append(domino)
        for other in domino_neighbours[domino]:
            if other in active_degrees[degree[other]]:
                active_degrees[degree[other]].remove(other)
                degree[other] -= 1
                active_degrees[degree[other]].add(other)                
    # Теперь перебираем в обратном порядке и либо красим в еще не занятый цвет,
    # если есть свободный из 5 цветов, иначе находим цепочку из чередующихся цветов,
    # которые могут быть перекрашены. Такая найдется в силу планарности
    colors = [-1 for domino in domino_tiles]
    slices = [draw_filling(result)]
    for domino in reversed(reversed_order):
        used_colors = [colors[other] for other in domino_neighbours[domino] if colors[other] != -1]
        domino_color = len(used_colors)
        for i, color in enumerate(sorted(set(used_colors))):
            if i != color:
                domino_color = i
                break
        if domino_color < 5:
            colors[domino] = domino_color
            for x, y in domino_tiles[domino]:
                result[x][y] = domino_color
            slices.  1
            for x, y in domino_tiles[other]:
                result[x][y] = color[other]
        color[domino] = c
        for x, y in domino_tiles[domino]:
            result[x][y] = c
        slices.append(draw_filling(result))
    return result, slices      

Если вы собираетесь использовать этот код, то обратите внимание, что там происходит отрисовка каждого шага — это было нужно для анимации, что сильно замедляет алгоритм. Если вам нужна только конечная покраска, то уберите весь код, задействующий переменную slices.

Ну и наконец попробуем один из примеров, который был чуть раньше

Сколько домино вам нужно для 2 игроков в мексиканском поезде?

Чтобы два игрока могли сыграть в мексиканский поезд, вам понадобится 91 домино.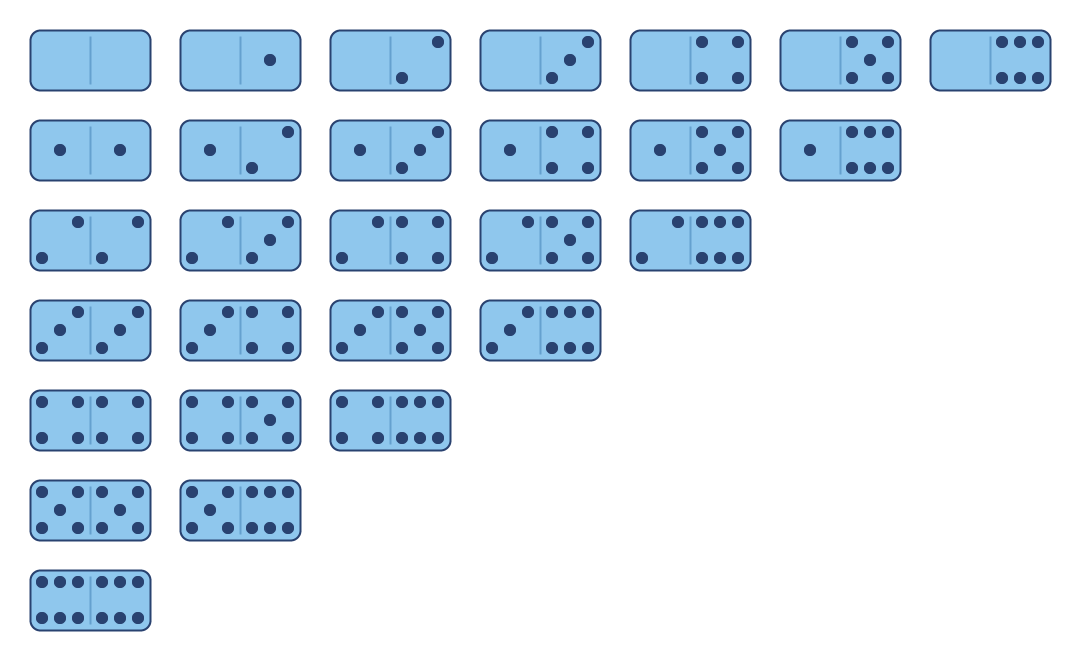 Набор домино должен состоять из домино, пронумерованных от двойного пробела до двойного двенадцати. В «Мексиканском поезде» используется все 91 костяшка домино, поэтому для игры вам понадобится полный набор.

Игра начинается с того, что каждый игрок вытягивает по семь костяшек домино, и игрок с наибольшим удвоением начинает игру. После первой игры домино перетасовываются, и каждый игрок будет тянуть домино до тех пор, пока не соберет полное количество плиток либо в руке, либо в своем личном поезде.

Содержание

Как играть вдвоем в домино «Мексиканский поезд»?

Игра в домино «Мексиканский поезд» с двумя игроками может быть очень увлекательной и отличным способом скоротать время! Для начала каждый игрок должен перетасовать свой набор костяшек и разделить их на две части, используя по 4-5 костяшек на каждую руку.

Положите оставшиеся костяшки лицевой стороной вниз, и каждый игрок одновременно возьмет по одной из стопки, чтобы у каждого игрока было две руки с одинаковым количеством костяшек домино. Первым ходит игрок с самым высоким двойным домино, а затем очередь переходит к следующему игроку.

В свой ход вы должны вытащить костяшку костяшки из кладбища, а затем сыграть в домино либо на собственном поезде, либо на поезде другого игрока. Если вы не можете сыграть в домино, вы должны пропустить свой ход. Когда все домино в поезде разыграны, побеждает игрок с наименьшим количеством очков.

После первого раунда продолжайте играть раунды, пока один из игроков не избавится от всех костяшек домино. В конце игры побеждает игрок с наименьшим количеством очков. Чтобы вести счет, сложите концы всех костяшек домино в руках игроков.

Игрок с наименьшей суммой становится победителем.

Домино «Мексиканский поезд» — это веселая и простая в освоении игра, в которую могут играть два игрока. Немного стратегии и удачи, и вы сможете играть часами!

Можно ли играть в домино с двумя людьми?

Да, вы можете играть в домино с двумя людьми. Dominoes Train — это динамичная игра в домино, в которую обычно играют от 2 до 4 игроков. Это все о том, чтобы строить поезда и блокировать поезда вашего противника, пытаясь первым избавиться от всех ваших домино в игре.

В этой игре каждый игрок стремится первым разыграть все костяшки домино в руке. С двумя игроками игра требует, чтобы каждый игрок собирал поезд из двух частей из одного и того же двойного домино. По ходу игры, если не осталось двойников, игрок должен сделать самый длинный поезд за свой ход.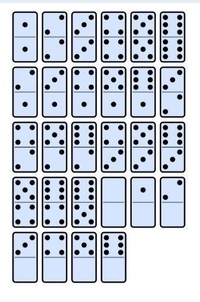

Чтобы выиграть, игрок должен положить все свои костяшки домино и первым крикнуть «Поезд. “.

Сможете ли вы поиграть на мексиканском поезде, прежде чем пустить свой собственный?

Да, вы можете играть на мексиканском поезде, прежде чем запускать свой собственный. В зависимости от правил игры вы можете пересесть на мексиканский поезд другого игрока, прежде чем начать свой собственный. Как правило, это требует, чтобы вы сбросили маркер на мексиканский поезд, прежде чем разыграть одну плитку.

Возможно, вы сможете играть на чужом мексиканском поезде, а не начинать свой собственный, как только игра начнется. При перемещении вашего поезда важно помнить, что вы можете добавлять на мексиканский поезд только те плитки, которые соответствуют двойнику, который был изначально размещен там.

Кроме того, нельзя снимать плитки с мексиканского поезда, если они уже установлены.

Вам нужно покрыть дубль в мексиканском поезде?

Нет, в мексиканском поезде не нужно оплачивать дубль. Вместо этого первый игрок, положивший двойную или более крупную кость, объявляет ее, а следующий игрок должен закрыть ее другой плиткой с тем же номером, но другого цвета.

Это можно назвать «легингом», так как дубль должен быть сделан одним и тем же игроком. Однако, если следующий игрок не делает дубль, то вызывающий дубль должен покрыть его своим дублем.

Если вызывающему не удается покрыть двойную на своем следующем ходу, следующий игрок в очереди должен покрыть двойную, и эта схема продолжается до тех пор, пока она не будет легирована.

Каковы правила игры в домино на двоих?

Правила игры в домино для 2 игроков довольно просты, и главная цель состоит в том, чтобы первым избавиться от всех костей домино из руки. Как правило, вы и ваш оппонент получаете по 7 костяшек домино для начала игры.

Прежде чем официально начать игру, необходимо определить так называемую «спиннер» или «ведущую» костяшку домино. Это делается путем размещения всех костяшек домино лицевой стороной вниз, и оба игрока случайным образом выбирают одну из них. Игрок с костяшкой с большим номером становится ведущим, после чего начинается игра.

Игра начинается с того, что ведущий игрок кладет на стол костяшку, один конец которой соединяется с открытыми концами трех костяшек костяшки, составляющих спиннер. Двигаясь по часовой стрелке, последующие игроки должны соответствующим образом совместить свои открытые концы.

В случае, если игрок не может создать совпадение, он должен либо взять новую костяшку с кладбища, либо «пропустить» свой ход.

Сколько игроков для бейсбола

Включите JavaScript

Сколько игроков для бейсбола

Игра завершается, когда игрок успешно создал комбинацию, в которой не осталось костяшек домино. Главный победитель выходит из раунда с очками от суммы рук всех его противников. Если игрок исчерпал всю кладовку (кучу неразыгранных домино) и по-прежнему не может сопоставить ни одну из своих костяшек, игра заканчивается вничью, и очки раунда делятся поровну между обоими игроками.

Это практически все, что вам нужно знать, чтобы начать играть в классическую игру в домино с двумя игроками. Наслаждаться!

Игра в домино только для двоих?

Нет, в домино могут играть двое и более человек. Домино — классическая игра, восходящая к древнему Китаю, в которую традиционно играют с набором из 28 плиток. Каждая плитка имеет две стороны домино — одна из них украшена 0, 1, 2, 3, 4, 5, 6 или 7 точками.

В зависимости от количества игроков в игру можно играть с дабл-шестеркой (28 плиток), дабл-девяткой (55 плиток), дабл-двенадцатью (91 плитка) или дабл-пятнадцатью (136 плиток). Сложность игры увеличивается с количеством плиток.

В домино можно играть более чем двумя игроками, при этом оптимальной группой может быть от трех до четырех игроков. В этом случае игроки по очереди тянут и кладут плитки на стол, каждый из которых стремится получить наибольшую общую стоимость в конце игры.

Существуют различные варианты костяшек домино, и многие из них можно настроить для разного количества игроков в игре.

Могут ли 5 ​​человек играть в Мексиканский поезд?

Да, в «Мексиканский поезд» могут играть 5 человек. В этой динамичной игре в домино требуется от двух до восьми игроков, поэтому она отлично подходит для групп разного размера. В игре каждый игрок получает набор костяшек домино с одинаковым числом.

Цель игры состоит в том, чтобы составить цепочки, похожие на поезда, из костяшек домино. Игроки получают очки за количество домино в каждом поезде и за все кости домино, оставшиеся в их руке к концу раунда. На игровое поле помещается специальный маркер — мексиканский поезд, и игроки должны прикрепить к нему домино или его продолжение, когда это возможно.

Игра — отличный способ весело провести время с семьей и друзьями, тренируя свой мозг с помощью стратегии и решения проблем.

Сможете ли вы запустить мексиканский поезд в свой первый ход?

Нет, вы не можете запустить мексиканский поезд в свой первый ход. Согласно традиционным правилам, в первый ход необходимо выложить один маркер (также известный как «так»), а затем последующие ходы должны добавлять маркеры к выложенной фишке.

После второго хода Мексиканский поезд можно запустить, добавив маркер к любой фишке. Таким образом, самый ранний ход, когда игрок может запустить мексиканский поезд, приходится на третий ход. Также важно помнить, что для запуска мексиканского поезда на доске должно быть не менее двух фишек с маркерами.

Каковы правила игры в домино «Мексиканский поезд»?

Домино «Мексиканский поезд» — это забавная игра, в которую играют с полным набором из двойных двенадцати костей домино. Игра подходит для 2-8 игроков и наиболее интересна, когда в нее играют от 6 и более игроков.

В начале игры каждому игроку раздается по 12 костяшек домино, которые он должен затем разложить в один или несколько рядов в том же порядке, что и костяшки в руке. Цель игры состоит в том, чтобы стать игроком с наименьшим количеством очков в конце игры.

Каждый ход начинается с того, что игрок, у которого есть «паровозик» — доминошка с двумя пробелами, запускает «поезд». Этот игрок должен положить на стол действующую костяшку домино из своей руки, и это будет началом поезда.

Последующие игроки должны по очереди садиться в поезд. Все игроки должны разыграть действительное домино в поезде или пройти. Домино должно совпадать с предыдущим сыгранным домино по количеству точек и может быть либо в том же направлении, что и первоначальный поезд, либо в противоположном направлении.

Если у игрока есть более одного действительного домино, он может играть более чем в одно домино. Игрок также может выбрать «зазвонить» другой поезд, если у него есть двойник, запуская новый поезд параллельно исходному поезду.

Если все игроки пасуют, игра переходит к человеку слева от игрока, запустившего поезд. Этот игрок должен запустить новый поезд, но не может играть ни в какое другое домино, если у него нет более одного действительного домино для игры.

Игра окончена, когда у игрока закончились костяшки домино или когда кто-то сыграет последнюю костяшку, а у каждого последующего игрока не осталось костяшек домино. Игрок с наименьшей суммой очков в конце игры объявляется победителем.

Какая самая простая игра в домино?

Простейшая игра в домино — Ничья. Draw Dominoes — классическая игра, но очень простая. Традиционно это игра для двух игроков, но в нее можно играть втроем или вчетвером. Все, что нужно, это 28 стандартных костяшек домино с двойными шестью и двойными двенадцатью.

В начале игры каждому игроку раздается по семь плиток, а остальные кладутся лицевой стороной вниз в центр стола. Цель игры состоит в том, чтобы стать первым игроком, который освободит свою руку от всех своих плиток.

Игроки по очереди тянут либо из стопки в середине стола, либо из руки противника, и берут сразу две плитки, чтобы добавить к своей руке. Затем они кладут одну плитку на стол, а другую оставляют в руке.

На столе первый игрок начинает с того, что кладет плитку из своей руки, которая имеет совпадающий пронумерованный конец, с открытым концом за столом. Раунды продолжаются до тех пор, пока у одного из игроков не закончатся плитки в руке, а его противник не сможет продолжить.

Игрок, у которого не осталось фишек в руке, становится победителем игры.

Почему поезд называется мексиканским?

Игра «Мексиканский поезд» названа так потому, что в ней используется манера игры, имитирующая поезд из деталей, выходящих из центрального узла. Этот поезд можно построить из «домино», маркеров или других деталей.

В начале игры игрок кладет двойную костяшку в центр стола, а каждый оставшийся игрок (по часовой стрелке от первого игрока) выкладывает свои «поезда» фишек из двойной костяшки, расширяя на все направления.

Собственный поезд игрока не может быть заблокирован фигурами других игроков, и цель состоит в том, чтобы соединить все свои части вместе в самую длинную цепочку или «поезд». Вот почему он называется «Мексиканский поезд»: каждый игрок протягивает свои «пути» из центральной точки, и повороты в игре могут проходить по множеству путей, как поезд, бегущий по ландшафту.

Bulk Dominoes — ведущий производитель костяшек домино. США – bulkdominoes.com

Скидка 17%

Скидка 17%

Скидка 33%

Распродано

Скидка 25%

Скидка 27%

Пусковое устройство

Обычная цена

29,99 долларов США

Цена продажи

29,99 долларов США

Обычная цена

Сохранить-Бесконечность

Распроданный

Цена за единицу товара

/отсутствует перевод: en. general.accessibility.unit_price_separator 

Выберите опцию

Название по умолчанию — 29,99 долларов США

Количество

— +

Более 160 советов и подсказок, чтобы стать мастером опрокидывания домино!

Станьте мастером сборки домино и усовершенствуйте свои методы сборки домино с помощью этого простого руководства с советами и рекомендациями. Внутри вы обнаружите все лучшие приемы, используемые для создания потрясающих и сложных цепных реакций домино и установок мирового класса. С более чем 160 трюками, которые можно связать вместе, чтобы создать тысячи различных комбинированных трюков, вы обязательно удивите всех, кто смотрит!

Складывать и опрокидывать кинетическое домино  – это весело и легко! С неограниченным количеством творческих игр с открытым концом вы можете строить извилистые дорожки, цепные реакции, суперспирали, пирамиды, стены, башни, трехмерные структуры и многое другое! Играть в домино легко и требует зрительно-моторной координации, внимания, уравновешенности, терпения и STEM/STEAM. Наблюдать за падающими костяшками домино невероятно приятно, когда они опрокидываются в завораживающем отображении движения и звука. В Kinetic Domino можно весело провести время с друзьями или всей семьей!

Независимо от того, являетесь ли вы опытным мастером игры в домино или только начинаете, эта книга является основным источником информации обо всем, что связано с домино.

• 60 больших домино PRO-Scale Kinetic Stacking Dropling Chain Reaction
• Игрушка STEM & STEAM – (Наука, технология, инженерия, искусство, математика).
• Удачи! При сборке и игре с Kinetic Dominoes он задействует зрительно-моторную координацию, концентрацию, устойчивость, терпение и STEM / STEAM. Домино демонстрирует законы движения, причины и следствия, все время просто играя и получая удовольствие.
• Проектируй, строй, сноси и удивляй! Настройте и сложите Ultimate domino run, а затем начните веселье с цепной реакцией, сбивая все это в изумлении.
• НАШЕ КАЧЕСТВО — Изготовлено из нетоксичных и безопасных для детей материалов Сделано в США с ответственным производством .
• Более 160 советов и рекомендаций
• Пошаговые инструкции
• Размер книги — 9″ X 12″ 
• Страниц — 136
• Полноцветная печать
• Сделано в США

Скидка 29%

Скидка 27%

Скидка 20%

Скидка 10%

Скидка 24%

Скидка 24%

Скидка 24%

Скидка 24%

Хотите купить костяшки домино оптом? Вы находитесь в правильном месте! У нас есть высококачественные штабелируемые и опрокидываемые плитки домино в десятках ослепительных цветов.