Принцип игры сапер: Сапер - подробные правила игры
Продвинутая тактика игры в «Сапёр» / Хабр
[Пятничный перевод статьи 1999 года одного из авторов движка игры Thief Шона Барретта]
Неприятное положение в «Сапёре»
В этом положении я знаю, что вокруг меня есть куча мин, но не могу определить, где они находятся. Несколько мин может быть в одном из двух мест (розовые или голубые), группа мин может быть расположена в одной из двух комбинаций (светло-/тёмно-зелёные). Кроме того, есть ещё сложная ситуация с «5» и «6» в левом верхнем углу, которую я никак не выделил.
Голубые/розовые — взаимоисключающие пары, светло-/тёмно-зелёные — взаимоисключающие группы
«Сапёр»: логика или вероятность
В «Сапёра» можно играть двумя способами: как в логическую или в вероятностную игру.
Технически, вероятность подразумевает логику. Если вы можете логически доказать, что мина должна находиться в определённом месте, то вероятность равна 100%. Если можете доказать, что её в этом месте нет, то вероятность равна 0%. То есть в каком-то смысле для нас важны только вероятности. Тем не менее, игрок для распознавания таких стопроцентных ситуаций игрок использует логическую дедукцию. Иногда, особенно на низких уровнях сложности, её достаточно для прохождения уровня, никакого подсчёта вероятностей не требуется.
Если можете доказать, что её в этом месте нет, то вероятность равна 0%. То есть в каком-то смысле для нас важны только вероятности. Тем не менее, игрок для распознавания таких стопроцентных ситуаций игрок использует логическую дедукцию. Иногда, особенно на низких уровнях сложности, её достаточно для прохождения уровня, никакого подсчёта вероятностей не требуется.
Но бывают такие ситуации, когда вся логика мира не может вас спасти. Простой пример — ситуация с «T», которую видно внизу по центру. Она немного осложняется дополнительными соседними минами. (В простейшем случае «2» заменяется на «1», а «5» — на «3», чтобы ситуация была симметричной.)
Нет никакого способа получить больше информации о вероятном положении одной мины, оставшейся в одной из этих клеток. Шансы пятьдесят на пятьдесят — можете бросать монетку. Когда у вас получается что-то подобное, лучше сразу же сделать выбор и не откладывать на потом. Если догадка будет неверной, то вы хотя бы сэкономите время на решение остальной части поля.
Тактика в конце игры
В эндшпиле можно использовать очень простую тактику — считать количество оставшихся мин. Допустим, я решил всё, кроме правой нижней части поля. Здесь может быть всего две конфигурации мин, соответствующих данным:
Возможные конфигурации мин в правом нижнем углу
Если у вас получилась такая позиция и счётчик говорит, что осталось всего две мины, то ответ готов: это должна быть конфигурация B.
Если счётчик говорит, что осталось три мины, то это необязательно конфигурация A. Это может быть схема B с оставшейся миной в одной из правых нижних групп клеток 3×3.
На самом деле, шансы в пользу конфигурации B.
Локальные вероятности
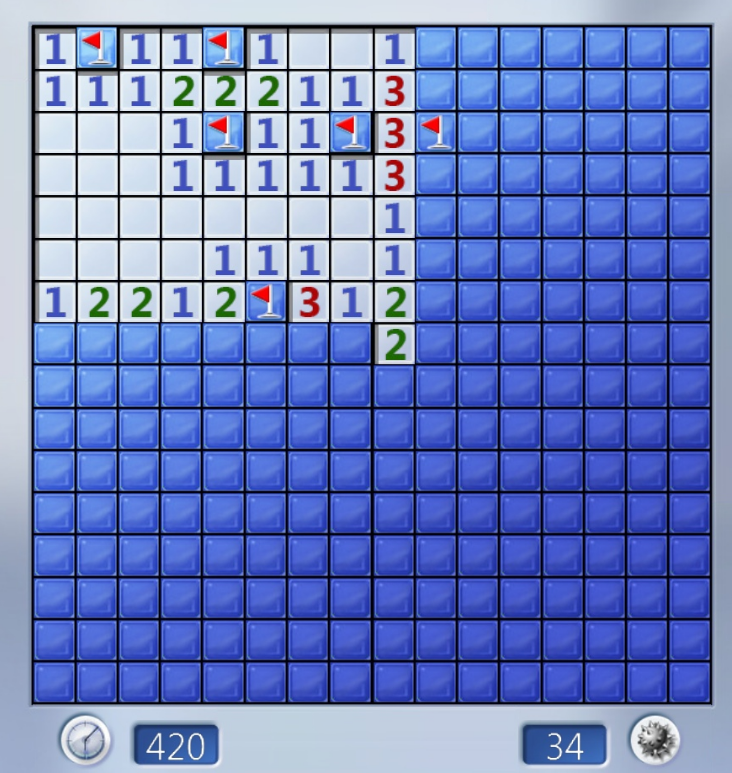 Говоря «локально», я подразумеваю, что если рядом с двумя неизвестными клетками есть «1», то вероятность спрятанной мины у каждой из них равна 50%.
Говоря «локально», я подразумеваю, что если рядом с двумя неизвестными клетками есть «1», то вероятность спрятанной мины у каждой из них равна 50%.Именно такая ситуация сложилась внизу в центре: каждая из соседних клеток, соседних к неизвестной паре, содержит в точности одну мину, то есть каждый из соседних фрагментов данных предполагает 50-процентную вероятность. В самом левом верхнем углу похожая ситуация:
С абсолютной точностью в каждом из розовых овалов есть по одной мине, то есть всего осталось 7 мин
Ситуация в правом нижнем углу тоже чем-то похожа: рядом с каждым из чисел на «границе» есть одна мина и две клетки, в которых она может быть.
Если рядом с клеткой есть одна скрытая мина, но три закрытых клетки, то вероятность мины в каждой из клеток составляет 33%; каждая из четырёх закрытых клеток имеет вероятность 25%. Если у нас две скрытые мины и три закрытых клетки, то каждая клетка имеет вероятность 66%.
Вот ситуация с «локальной вероятностью» для всего поля:
Как вы видите, несколько клеток в верхней левой области имеют несколько вероятностей; закрытая клетка рядом с «2» и «6» и одна рядом с «3» и «5». (Клетка рядом с «5» и «6» благодаря им всё равно имеет вероятность 66%, поэтому нет видимого несоответствия.)
(Клетка рядом с «5» и «6» благодаря им всё равно имеет вероятность 66%, поэтому нет видимого несоответствия.)
Разрешение конфликтов локальной вероятности
Вы наверно, задаётесь вопросом, что значит наличие конфликтующих локальных вероятностей. Интуиция может подсказать, что наибольшая вероятность должна выиграть. Например, клетка между «6» и «2» должна на самом деле иметь 66%. Это будет значить, что у крайней левой клетки с вероятностью 50% она на самом деле равна 33%. Или можно попробовать как-то комбинировать приоритеты: возможно, вероятность будет 5/6 или средним значением.
Но ничто из этого на самом деле неверно. Данные, из которых получены вероятности, не независимы друг от друга, поэтому никакие прямолинейные математические расчёты не будут верными. Причина правильности локальной догадки о 50% внизу в центре в том, что она действительно независима ни от чего другого. Если случайным образом воссоздавать поле по уже имеющимся у нас данным, то ровно в половине из моделей мина будет в одной из двух клеток. (Вероятность иногда запутывает людей, которые не могут разобраться, какие правила расчёта вероятностей применимы в конкретной ситуации. Такой подход — это гарантировано верный путь, потому что он основан на определении вероятности в статистическом прогнозировании: вычисление выполняется измерением во всех возможных конфигурациях, которые могли привести к текущей ситуации, при этом все они считаются одинаково вероятными.)
(Вероятность иногда запутывает людей, которые не могут разобраться, какие правила расчёта вероятностей применимы в конкретной ситуации. Такой подход — это гарантировано верный путь, потому что он основан на определении вероятности в статистическом прогнозировании: вычисление выполняется измерением во всех возможных конфигурациях, которые могли привести к текущей ситуации, при этом все они считаются одинаково вероятными.)
То есть для верных измерений в ситуации в левом верхнем углу нужно рассмотреть все возможные конфигурации мин, удовлетворяющие уже собранным данным, а затем посчитать, какой процент из них содержит мину в нужной позиции.
Непосредственный подсчёт потребовал бы много времени. К счастью, существуют и другие способы.
Подсчёт конфигураций
Абстрактный способ вычисления вероятностей заключается в обходе всех возможных конфигураций мин, отбрасывании конфигураций, не отвечающих собранным данным, и вычислении статистики для каждой из возможных позиций.
Более практичный подход — рассматривать только те варианты, которые нельзя отбросить. Для этого нам нужно применить логику и сгенерировать все возможные ситуации, которые могут соответствовать имеющимся данным. Я уже показывал два варианта для правого нижнего угла, а вот вероятности для левого верхнего:
Возможные конфигурации для левого верхнего угла
(Как и раньше, овал высотой в две клетки показывает, что мина может с одинаковой вероятностью находиться в любой из клеток. Я мог бы перечислить каждый из двух этих случаев отдельно, то есть получилось бы 10 конфигураций, но никакой пользы в этом для нас нет. Структура таблицы: два ряда (пронумерованные как «1» и «2») отличаются положением мины в четвёртом ряду. Три столбца характеризуются положением мин во втором ряду.)
Теперь есть искушение воскликнуть: «ага, вот пять случаев, так что мы можем подсчитать количество случаев для каждой из возможных позиций мины». Например, мина находится в четвёртом ряду (рядом с левой нижней «1») находится слева в двух верхних случаях, и справа в трёх нижних случаях.
Однако мы упускаем одну тонкость — количество мин в некоторых случаях разное: в A1 шесть мин, в B2 — четыре, и по пять во всех остальных случаях.
Считаем ненайденные мины
Для подробного изучения этой тонкости давайте вернёмся к более простой ситуации в правом нижнем углу.
Возможные конфигурации с правом нижнем углу
Предположим, что я уже открыл остальное поле и знаю, что осталось ровно три мины.
Есть искушение предположить, что наиболее вероятна конфигурация A ровно с тремя минами. Но это неверно.
 Однако достаточно сказать, что в действительности шансы в этой ситуации не зависят от общего количества мин и размера поля.
Однако достаточно сказать, что в действительности шансы в этой ситуации не зависят от общего количества мин и размера поля.Правильный ответ таков: сколько возможных конфигураций из трёх мин соответствуют нашим знаниям о поле? Из рисунка мы видим, что две: конфигурации A и B. Но в B всего две мины. Третья мина может быть в любой из клеток нижней области 3×3, о которой мы пока не собрали никаких данных. То есть всего есть девять вариантов конфигураций B, я просто не стал изображать их все.
Следовательно, существует всего десять возможных конфигураций. Каждая из десяти конфигураций равновероятна. (Как я упоминал ранее, это критически важно для понимания вероятности. Шансы того, что компьютер сгенерировал любой из этих вариантов малы, но они равно малы, потому что компьютер [насколько мы знаем] давал
каждой конфигурации равные шансы. Вы с равной вероятностью можете выбросить конфигурацию из десяти «орлов» подряд и последовательность два «орла», одна «решка», один «орёл», три «решки», один «орёл», одна «решка» и один «орёл». Вероятнее выбросить в сумме пять «орлов» и пять «решек», но не никакую конкретную последовательность «орлов» и «решек». В «Сапёре» мы имеем дело с конфигурациями мин, которые похожи на последовательности бросков монеты.)
Вероятнее выбросить в сумме пять «орлов» и пять «решек», но не никакую конкретную последовательность «орлов» и «решек». В «Сапёре» мы имеем дело с конфигурациями мин, которые похожи на последовательности бросков монеты.)Поскольку каждая из десяти конфигураций (девять для B, одна для A) равновероятны, конфигурация B в данном случае имеет вероятность 90%!
Если бы на этом этапе было четыре мины, то у конфигурации
С пятью минами конфигурация A имела бы 36 вариантов, а конфигурация B — 9*8*7/6 = 84 варианта; то есть шансы B были бы чуть больше 66%.
В случае шести мин B имела бы вероятность 60%. С семью минами у B было бы всего 50%. С восемью минами B была бы менее вероятна, чем A; в этом случае с таким количеством мин в оставшихся позициях конфигураций становится меньше. Рассмотрим наихудший случай, когда осталось 11 мин. (Шанс этого чрезвычайно мал, но если такая ситуация возникнет, то применимы эти вероятности.) В конфигурации B, во всех закрытых клетках будут мины, в конфигурации A во всех, кроме одной. То есть существует 9 вариантов для A и всего один для B.
С восемью минами B была бы менее вероятна, чем A; в этом случае с таким количеством мин в оставшихся позициях конфигураций становится меньше. Рассмотрим наихудший случай, когда осталось 11 мин. (Шанс этого чрезвычайно мал, но если такая ситуация возникнет, то применимы эти вероятности.) В конфигурации B, во всех закрытых клетках будут мины, в конфигурации A во всех, кроме одной. То есть существует 9 вариантов для A и всего один для B.
Окончательное решение
На имеющемся у нас поле осталось девять мин. Одна из них находится в центральной нижней области, и её положение полностью независимо, поэтому можно его игнорировать. То есть мы рассматриваем всё поле, кроме этого случая: не найдено всего восемь мин. (Чтобы не возникло путаницы, я продолжу явным образом считать овал в левом верхнем углу, потому что это изображение левого верхнего угла.)
Может сложиться любая комбинация из левой верхней и правой нижней конфигураций, за исключением одной из них (A1 + A), для которой потребуется девять мин. Поэтому мы должны перечислить каждую из этих возможных конфигураций и сосчитать оставшиеся мины и закрытые клетки.
Поэтому мы должны перечислить каждую из этих возможных конфигураций и сосчитать оставшиеся мины и закрытые клетки.
На самом деле, количество закрытых клеток независимо: их девять в правом нижнем углу и три в левом верхнем, то есть всего 12.
| Вверху слева | Внизу справа | Количество мин | Осталось мин | Закрытые варианты |
|---|---|---|---|---|
| A1 | B | 8 | 0 | 1 |
| B1 | A | 8 | 0 | 1 |
| B1 | B | 7 | 1 | 12 |
| A2 | A | 8 | 0 | 1 |
| A2 | B | 7 | 1 | 12 |
| B2 | A | 7 | 1 | 12 |
| B2 | B | 6 | 2 | 66 |
| C2 | A | 8 | 0 | 1 |
| C2 | B | 7 | 1 | 12 |
Таким образом, всего существует 118 возможных комбинаций. Исходя из этого мы можем независимо посчитать количество комбинаций для каждой из левых верхних и правых нижних конфигураций:
Исходя из этого мы можем независимо посчитать количество комбинаций для каждой из левых верхних и правых нижних конфигураций:
| Конфигурация | Варианты | Процент |
|---|---|---|
| A1 | 1 | 1 |
| B1 | 13 | 11 |
| A2 | 13 | 11 |
| B2 | 78 | 66 |
| C2 | 13 | 11 |
| A | 15 | 13 |
| B | 103 | 87 |
Далее я обошёл каждую клетку на поле и вычислил её вероятность, суммировав количество вероятностей, в которых она появляется, и поделив на 118. (На самом деле, просто сложив указанные выше проценты.) Кроме того, в среднем в каждой из закрытых клеток есть мина в 15 из 118 вариантов (то есть шансы на то, что по крайней мере в одной закрытой клетке есть мина, очень высоки). [Это можно вычислить умножением количества оставшихся мин на закрытые варианты, что даёт нам среднее количество мин в закрытых клетках.]
[Это можно вычислить умножением количества оставшихся мин на закрытые варианты, что даёт нам среднее количество мин в закрытых клетках.]
Вероятности наличия мины
(Следует сказать, что это не показывает всей доступной информации. Например, мы знаем, что вероятности двух тёмно-зелёных клеток с 87% связаны — если одна верна, то другая тоже. И голубые 13-процентные клетки, в которых есть мины по конфигурации A, тоже связаны. Остальные голубые 13-процентные клетки не связаны. Если в одной из них есть мина, вероятность того, что в любой из оставшихся есть мина, уменьшаются.)
Играем в игру
Скорее всего, играя в «Сапёра», вы не захотите корпеть над всеми этими вычислениями.
И я тоже.
Но я действительно перечислил все возможные конфигурации в левом верхнем и правом нижнем углах. Я заметил, что в одной конфигурации (B2-B) используется на одну мину меньше, чем во всех остальных, и применил проверенное временем правило «меньше мин — значит, больше закрытых вариантов» (которое действует приблизительно пока количество закрытых клеток меньше чем удвоенное количество ненайденных мин). Это означает, что намного вероятнее конфигурации с меньшим количеством мин.
Это означает, что намного вероятнее конфигурации с меньшим количеством мин.
Поскольку в левом верхнем углу было множество конфигураций, определение шансов для любой клетки довольно сложно. Поэтому я просто выяснил, что конфигурация B в правом нижнем углу намного более вероятна, и случайно выбрал одну из подходящих клеток. (Я надеялся, что она позволит мне закончить правый нижний угол, а потом, вооружённый большей информацией о количестве оставшихся мин, я смогу завершить левый верхний угол, после чего мне придётся бросить монетку для выбора внизу в центре. Разумеется, в идеале нужно было выбрать клетку, максимизирующую вероятность получения полезной информации, но любая из этих догадок позволила бы мне «войти» в правый нижний угол для дальнейшего сбора данных.) Шансы были выше у конфигурации B, поэтому я выбрал клетку, в которой была мина в конфигурации A.
Восемь раз из девяти я был бы прав.
Сапёр (компьютерная игра) | это… Что такое Сапёр (компьютерная игра)?
Толкование
- Сапёр (компьютерная игра)
KMines 2.
 1.9
1.9Сапёр — компьютерная игра‐головоломка.
Содержание
- 1 Принцип игры
- 2 Варианты
- 3 Оценка сложности поля
- 4 Рекорды
- 5 Ссылки
- 6 Внешние ссылки
Принцип игры
Обычно двухмерное прямоугольное игровое поле поделено на клетки или другие части, некоторые из которых содержат скрытые мины. Игрок открывает клетки, стараясь не попасть на мину. Если игрок откроет клетку (или другую область) с миной, игра заканчивается. Если же мины нет, то в клетке появляется число, обозначающее количество мин в соседних клетках (в различных вариантах игры соседство может определяться по‐разному). Рассчитав при помощи таких чисел расположение мин, игрок может пометить соответствующие клетки специальной меткой, чтобы случайно не открыть их.
Варианты
Xbomb в режиме шестиугольников
emMines — трёхмерный вариант игры с изометрическим выводом
Один из режимов игры Minesweeper 3D
Windows Minesweeper в режиме «Новичок» (версия для Windows Vista)
Существуют варианты игры с полем и/или клетками непрямоугольной формы, или в более чем двухмерном пространстве.

При создании поля с помощью генератора случайных чисел может сложиться ситуация, когда игроку придётся угадывать, где находится мина. Некоторые реализации (например, «Mines» в наборе головоломок Саймона Тэтхема) позволяют этого избежать.
Оценка сложности поля
Часто сложность поля оценивают с помощью величины 3BV (Bechtel’s Board Benchmark Value). Эта величина численно равна минимальному количеству непосредственных открытий клеток, необходимому для полного решения поля. Следует отметить, что эта величина отображает лишь количество определенных действий в идеальном случае при определенной манере игры, а вовсе не трудность поля для решения конкретным игроком.
Рекорды
Основной целью игры является открытие всех клеток за как можно меньшее время. Поэтому рекорды для стандартных уровней сложности регистрируются разными обществами игроков. Для серьёзных соревнований используются версии игры, фиксирующие время прохождения с точностью до миллисекунд.
 Современная таблица рекордов выглядит следующим образом.[1]
Современная таблица рекордов выглядит следующим образом.[1]Сложность Параметры поля Рекорды Beginner Поле 9*9, 10 мин 0 секунд — достигнут многими игроками в случаях, когда поле открывается одним щелчком (стандартная версия Minesweeper for Windows в таких случаях показывает результат 1 секунда) Intermediate Поле 16*16, 40 мин 10,015 секунд — Kamil Muranski
9,890 секунд — Jake Warner (оспариваемый результат)Expert Поле 16*30, 99 мин 35.702 секунд — Kamil Muranski Результат сильно зависит от расположения мин. Теоретически, при любых игровых параметрах есть вероятность прохождения одним щелчком. Но практическая реализация генератора случайных комбинаций не позволяет получить слишком простую расстановку на больших досках. Поэтому результаты на второй и третьей сложностях хорошо отражают уровень игрока.

Ссылки
- ↑ Рекорды по «Сапёру»
Внешние ссылки
- Planet Minesweeper — Международный рейтинг лучших игроков в Microsoft Minesweeper (не обновляется)
- Российский рейтинг лучших «сапёров»
- On-line чемпионат по «сапёру»
- Умный Сапер-Минер
Wikimedia Foundation. 2010.
Игры ⚽ Нужен реферат?
- Сапфиры
- Сапёрная лопатка
Полезное
Как играть в Minesweeper
Minesweeper Rules
Minesweeper для Windows XP с 40 минами, разобранными за 28 секунд
Minesweeper — игра, в которой мины спрятаны в сетке квадратов. Безопасные квадраты имеют числа, говорящие вам, сколько мин касается квадрата. Вы можете использовать числовые подсказки, чтобы решить игру, открыв все безопасные квадраты. Если вы нажмете на мину, вы проиграете!
Windows Minesweeper всегда делает первый щелчок безопасным. Вы открываете квадраты левой кнопкой мыши и ставите флажки на мины правой кнопкой мыши. Повторное нажатие правой кнопки мыши превращает ваш флажок в вопросительный знак. Когда вы открываете квадрат, который не касается мин, он становится пустым, а соседние квадраты автоматически открываются во всех направлениях, пока не дойдут до квадратов, содержащих числа. Обычная стратегия для запуска игр состоит в том, чтобы щелкать случайным образом, пока не появится большое отверстие с большим количеством чисел.
Вы открываете квадраты левой кнопкой мыши и ставите флажки на мины правой кнопкой мыши. Повторное нажатие правой кнопки мыши превращает ваш флажок в вопросительный знак. Когда вы открываете квадрат, который не касается мин, он становится пустым, а соседние квадраты автоматически открываются во всех направлениях, пока не дойдут до квадратов, содержащих числа. Обычная стратегия для запуска игр состоит в том, чтобы щелкать случайным образом, пока не появится большое отверстие с большим количеством чисел.
Если вы отметите все мины, соприкасающиеся с числом, аккорд на число откроет оставшиеся квадраты. Аккорд — это когда вы нажимаете обе кнопки мыши одновременно. Это может сэкономить вам много работы! Однако, если вы разместите правильное количество флагов на неправильных квадратах, аккорды взорвут мины.
Три уровня сложности: начальный (8×8 или 9×9 с 10 мин), средний (16×16 с 40 мин) и эксперт (30×16 с 99 мин). Игра заканчивается, когда все безопасные квадраты открыты. Счетчик показывает количество мин без флажков, а часы показывают ваше время в секундах. Сапер сохраняет ваше лучшее время для каждого уровня сложности.
Сапер сохраняет ваше лучшее время для каждого уровня сложности.
Вы также можете играть в Пользовательские игры размером до 30×24 с минимумом 10 мин и максимумом (x-1)(y-1) мин.
Базовые узоры
Когда число касается одинакового количества клеток, эти клетки должны быть минами. Посмотрите на эти примеры:
1 в углу касается 1 клетки, значит, это мина.
Двойка касается двух квадратов, поэтому они оба должны быть минами.
3 касаются 3 квадратов, значит, все они должны быть минами.
4 касаются 4 квадратов, значит, все они должны быть минами.
5 касается 5 квадратов, значит, все они должны быть минами.
6 касается 6 квадратов, значит, все они должны быть минами.
7 касается 7 квадратов, значит, все они должны быть минами.
8 касается 8 квадратов, значит, все они должны быть минами.
Простой трюк — нажать обе кнопки («аккорд») на числе, чтобы надавить (но не открыть) квадраты, которых он касается. Это показывает, сколько квадратов касаются числа.
Это показывает, сколько квадратов касаются числа.
Розовая двойка касается трех клеток и не может быть собрана. Желтая 2 касается двух квадратов и может быть решена.
Розовая двойка касается трех квадратов и не может быть собрана. Желтая 3 касается трех квадратов и может быть решена.
Распространенная ошибка — видеть «фальшивую» 1 на углу, где 1 уже касается мины.
1 в углу уже касается мины. Розовый квадрат — это не мина.
1 в углу уже касается мины. Розовый квадрат — это не мина.
| Как играть в сапёра Расширенные шаблоны Первый клик Гадание Нет флагов Эффективность Советы Ссылки |
Теория игр: Сапер – Кассандра Джон
На работе в начале моей карьеры у меня было чудесное стечение обстоятельств, которое позволило мне а) многому научиться и б) корпоративной сети, которой еще не было полностью заблокирован, что предусматривало в) возможность играть часов часов в Сапера. [1], [2] Таким образом, я хочу поделиться с вами кое-чем интересным из этого набора квадратов 16 x 16.
[1], [2] Таким образом, я хочу поделиться с вами кое-чем интересным из этого набора квадратов 16 x 16.
1. Вы должны делать рывки – риск – это основа, а бездействие – это действие
Первый ход, который вы делаете в Minesweeper, это , это всегда догадка . Если этот шаг не открывает достаточно места для вас, чтобы сделать какой-либо настоящий «подметание», тогда вы знаете, что? Вы должны сделать этот прыжок веры и сделать еще одним предположением. Иногда это взрывает вас, иногда нет, но бездействие есть действие: если вы не пойдете на риск, вы не продвинетесь в игре.
Это так просто. Риски имеют основополагающее значение для игры; риски имеют основополагающее значение для выполнения работы на работе; риски имеют основополагающее значение для жизни и жизни.
2. Изучите правила, разберитесь в процессе – это не называется шахтой подметальная машина даром
Это не волей-неволей игра «выбери любую клетку» (по крайней мере, после начальных ходов, см. выше). Игра дает вам подсказки с числами: 1 означает, что одна клетка, касающаяся этой открытой клетки, имеет мину. Если есть только одна клетка, соприкасающаяся с этим открытым пространством, то вы знаете, что это клетка с миной! 2 означает два квадрата; 3 означает три квадрата и так далее и тому подобное.
выше). Игра дает вам подсказки с числами: 1 означает, что одна клетка, касающаяся этой открытой клетки, имеет мину. Если есть только одна клетка, соприкасающаяся с этим открытым пространством, то вы знаете, что это клетка с миной! 2 означает два квадрата; 3 означает три квадрата и так далее и тому подобное.
Как только вы узнаете правила, вы сможете придумать, как вы будете «подметать» игровое поле. Если вашей инженерной команде нравится оставлять «нераскрытыми» 2-недельные буферы в своих оценках, то вы знаете потенциальные области для ужесточения плана в случае необходимости. Если ваш менеджер говорит «может быть» и всегда имеет в виду «нет», то вы знаете, что возможно = нет. Продолжайте с этим знанием в виду.
3. Как только вы узнаете закономерности и будете следовать им, ваши шансы на успех значительно возрастут
Итак, вы взяли на себя риск, у вас есть открытые пространства для работы, вы понимаете правила и распознали свой процесс прохождения, и есть некоторые «шаблоны моего поведения», которые теперь очевидны. Другими словами, доска стала понятной, и вы знаете, как по ней ориентироваться.
Другими словами, доска стала понятной, и вы знаете, как по ней ориентироваться.
Я постоянно видел этот паттерн в Minesweeper:
Давайте предположим, что вокруг него серое/открытое пространство. Мины всегда на концах. Всегда . Никакие желания, планы, молитвы или надежды не изменят этого.
Теперь давайте перенесем этот шаблон в реальную жизнь. Как пример: у вас есть коллега, у которого вам нужно попросить об одолжении или сделать просьбу. Вы знаете, что этот коллега раздражителен и темпераментен еще до того, как выпил свою первую утреннюю чашку кофе. Не могли бы вы подойти к нему в тот момент, когда он сядет на стул, все еще в пальто, и сделать эту просьбу?
Нет! Либо вы ждете, пока кофеин сделает свое дело или ты иди принеси ему эту чашку кофе сначала.
Вы не можете игнорировать правила, раз выяснив их суть. Это может быть медленно (ожидание кофеина), и это может быть похоже на два шага вперед, три шага назад и один шаг в сторону, чтобы продвинуться на четыре шага вперед. Но ничего страшного: с практикой все в порядке, и ты станешь лучше в танце (он приходит в 7:05 каждое утро, его ждет чашка кофе).
Но ничего страшного: с практикой все в порядке, и ты станешь лучше в танце (он приходит в 7:05 каждое утро, его ждет чашка кофе).
4. Иногда, в конце концов, вам просто нужно идти на поводу у своей интуиции
Если вы играли в столько же игр в «Сапёра», сколько я (не буду признавать количество), то вы знаете, что, несмотря на все ваши навыки, иногда вы доберетесь до этого:
Это невозможное положение . Это 50/50; это и то и другое. Вы не знаете. Вы не можете знать. Но помните: бездействие — это действие, поэтому вы не можете мешкать с этим вечно (секунды идут!) и вы не можете выиграть, если не сделаете ход.
Следуйте своей интуиции.
Mineswept
Итак, если у вас есть несколько минут свободного времени, а на вашем компьютере все еще есть Minesweeper, я бы посоветовал вам сыграть в игру. На самом деле, я бы посоветовал вам сыграть несколько раундов; это, конечно, простая игра, но вы можете многому научиться:
Рискните , потому что ничто не может начаться или продолжиться без действия. Изучите правила , слушая, обращая внимание, делая и да, даже терпя неудачу. Доверяйте процессу после того, как вы его распознали, потому что определенные шаблоны повторяются, и если вы научитесь работать с ними, ваши шансы на успех возрастут намного, намного выше. И, наконец, что не менее важно, прислушивайтесь к своей интуиции , потому что иногда нет четкого правильного или неправильного ответа.
Изучите правила , слушая, обращая внимание, делая и да, даже терпя неудачу. Доверяйте процессу после того, как вы его распознали, потому что определенные шаблоны повторяются, и если вы научитесь работать с ними, ваши шансы на успех возрастут намного, намного выше. И, наконец, что не менее важно, прислушивайтесь к своей интуиции , потому что иногда нет четкого правильного или неправильного ответа.
Если вы все правильно поняли, фантастика! Вы заслуживаете похвалы, которая приходит с чистым, явным успехом.
И если вы ошибетесь, не позволяйте этому сломить вас: это всего лишь игра. И хотя работа и жизнь — это не «просто игры», они также не являются абсолютной игрой с нулевой суммой. Если вы ошибетесь частично или даже полностью, я обещаю вам, будут другие шансы и другие возможности, и то, что вы узнали, останется полезным.
Счастливого траления!
________
[1] Обратите внимание, я не призываю играть в игры на работе; Я работал слишком много часов, и у меня было слишком много телефонных конференций.

 1.9
1.9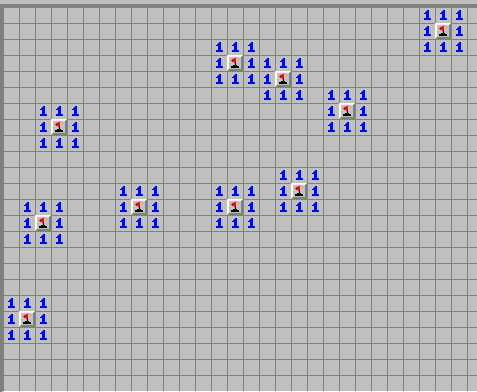
 Современная таблица рекордов выглядит следующим образом.[1]
Современная таблица рекордов выглядит следующим образом.[1]