Правила игры сапер на компьютере: Как играть в Сапера

Как решить «Сапёра» (и сделать его лучше) / Хабр

«Сапёр» (Minesweeper) — это простая игра с простыми правилами, однако некоторые её конфигурации создают любопытные трудности. В этой статье мы создадим солвер «Сапёра» с увеличивающейся сложностью, и поразмышляем над тем, как меняется динамика игры при постепенном повышении уровня помощи. В конце мы разработаем новый вариант игры с гораздо более интересным геймплеем.

Локальные рассуждения: ноль соседних мин

В оригинальной игре используется один автоматический механизм: когда игрок открывает клетку, рядом с которой нет мин, движок игры открывает все соседние клетки. Это ничем не угрожает игре, поэтому можно спокойно позволить компьютеру это сделать, а сама ситуация сразу же понятна игроку и никак не мешает геймплею.

Такое рассуждение совершенно локально: для принятия решения о следующем действии учитывается информация только одной клетки.

Сложно придумать ситуацию, в которой игра стала бы хуже без этой автоматической помощи. Попробуйте сыграть в такую игру, чтобы получить представление о том, как она проходит без автоматического открытия клеток [в оригинале статьи все примеры интерактивны]:

Локальные рассуждения с учётом окружения

Новому игроку несложно будет понять, что если количество соседних мин, то есть число, показанное в клетке, равно количеству неоткрытых соседних клеток, то все эти клетки должны быть минами, поэтому на них надо поставить флажки. Аналогично, когда количество соседних мин равно количеству соседних флагов, то оставшиеся неоткрытыми соседние клетки должны быть пусты.

В этих правилах учитывается одна клетка, а также состояние соседних (открыты/поставлен флажок).

Реализация этих правил вручную может быть увлекательной. Если добавить таймер, то игрок начинает учиться применять их быстро и точно. Это превращает «Сапёра» в игру на реакцию.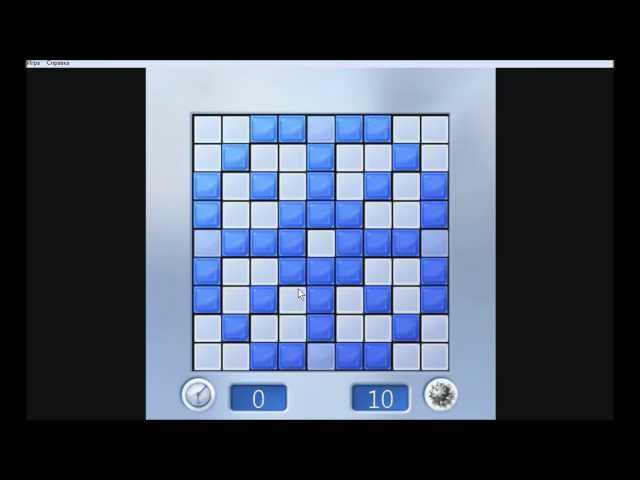

Что произойдёт, если мы автоматизируем эти правила?

У подобной автоматизации есть интересный побочный эффект — установка флажка может мгновенно иметь фатальные последствия.

В остальном у нас могут возникнуть ситуации, которые можно разбить на три категории:

1. Игры, полностью разрешаемые применением автоматических правил
2. Сложные ситуации, требующие для рассуждений большего количества клеток
3. Состояния игры, в которых нет логического пути вперёд — игроку остаётся только выбирать случайно, возможно с учётом вероятностей.

Ситуация 1 кажется красивой, но не особо интересной, если будет возникать слишком часто. Будут ли такие игры лучше без автоматического решения? Может быть и нет; такие игры очень просты даже при решении вручную, и игроку не особо интересно играть в игры, в которых нет трудностей. Хотя, разумеется, в игре на реакцию сложность есть всегда: нужно действовать как можно быстрее.

Очень привлекательной мне кажется ситуация 2. Мы больше сосредотачиваемся на решении логических условий, меньше тратя время на точное прицеливание и нажимание правильных кнопок. Это делает «Сапёра» больше похожим на активную головоломку.

Ситуация 3 полностью разрушает всю увлекательность. Впрочем, я слышал, что некоторым людям нравится играть в игры со случайностью.

Можно ли избавиться от ситуации 3?

Полное решение: глобальные рассуждения

Для алгоритмического обнаружения всех необходимых для состояния игры логических условий нам нужно выполнить исчерпывающий поиск всех состояний игры. Доказано, что Minesweeper — это NP-полная задача. Ниже показан небольшой, но интересный и наглядный пример состояния игры, имеющий всего одно логическое решение, но для его нахождения необходимо учитывать состояние игры целиком:

Возможно ли выполнить поиск по всему пространству состояний игры? Сколько всего существует вариантов состояний s?

Дано:

w = ширина поля

h = высота поля

k = количество мин

n = w · h

Тогда количество возможных состояний s равно

Для стандартных уровней «Новичок», «Любитель» и «Профессионал» это даёт нам:

Мы понимаем, что наивный подход здесь совершенно не подходит. Давайте посмотрим, как бы мог выглядеть наивный алгоритм, и узнаем, можно ли его оптимизировать в нечто работающее.

Наивный алгоритм

Задача алгоритма — найти все необходимые для заданного состояния поля логические условия. Было бы сложно реализовать это тщательным продумыванием решений; компьютер гораздо лучше справляется с быстрым выполнением кучи глупых действий.

Что мы можем сделать «глупого»: сгенерировать все возможные перестановки позиций мин для всех оставшихся мин. Если такая перестановка соответствует всем открытым числам, то она будет правильным решением игры. Затем мы изучаем все возможные перестановки, находим все возможные решения, но по-прежнему не знаем, какое из них является верным.

Если во всех возможных решениях есть что-то общее, или среди открытых клеток, или среди клеток, помеченных как мины, то мы понимаем, что это общее должно быть частью верного решения для текущего поля. И в самом деле: невозможно создать верного решения, не имеющего таких совпадающих элементов, иначе бы мы их обнаружили.

Таким образом мы можем найти все необходимые для текущего состояния поля логические условия.

Клетки с ограничениями и без ограничений

У приведённого выше алгоритма есть очевидная проблема: количество состояний, которое ему нужно исследовать. Но не все клетки одинаковы. Неоткрытые клетки, находящиеся рядом с числом, очевидно ограничены этим числом. Мы назовём эти клетки ограниченными. Оставшиеся клетки мы назовём неограниченными.

Если мы реализуем приведённый выше алгоритм, но будем выполнять поиск только в пространстве состояний ограниченных клеток, и будем возвращаться назад, как только нарушим ограничение, то во многих играх сможем решить все логические условия за разумный промежуток времени:

В случае неограниченных клеток мы никак не можем узнать, где расположены мины, и логически сразу знаем об этом. Это означает, что можно исключить их из вычисления и рассматривать только расположение мин рядом с открытыми числами.

Однако мы знаем, что некое количество мин может попасть во множество неограниченных клеток; если есть 6 мин и 4 ограниченных клетки, то в ограниченных клетках может быть максимум 4 мины, то есть не менее 2 мин должно находиться в неограниченных клетках. По аналогичной логике мы иногда можем определить, что все неограниченные клетки должны быть пустыми или все содержать мины.

В показанном ниже случае мы знаем позиции всех мин, поэтому ИИ должен быть способен понять, что оставшиеся ячейки не заняты:

В следующем случае мы не знаем позиций всех мин, но можем понять, что оставшуюся мину нужно поместить в одну из двух клеток слева вверху. Это значит, что оставшаяся в правом нижнем углу клетка свободна:

Версия со случайностью

Если мы автоматически будем запускать глобальный солвер, то получим оптимизированную по случайности версию «Сапёра»:

Можно разделить игры в этой версии на три категории:

1. Игры, в которых игрок делает произвольный выбор и выигрывает.
2. Игры, в которых игрок делает произвольный выбор и проигрывает.
3. Игры, в которых работа ИИ требует много времени, и игрок на самом деле может использовать рассуждения.

Очевидно, что это игра со случайностями. В чём же привлекательность таких игр? С точки зрения логики показанная выше игра схожа с такой:

Но какая из игр со случайностями лучше? Похоже, что смысл других игр со случайностями заключается в существовании сложной связи между действиями игрока и победой/проигрышем. Для вытягивания номеров лотереи используются сложные машины, которые специально не торопятся в выборе номера и делают из показа этого номера целое шоу.

Возможно, большое поле, которое решается автоматически, является довольно хорошей игрой
со случайностями, учитывая то, что игрок наблюдает за постепенным открыванием всех клеток.

Можем ли мы придумать другой тип игры?

Детерминированная версия

Теперь у нас есть ИИ, способный определять все логичные шаги из заданного состояния игры. Иногда он не сможет находит логичных шагов. В таких ситуациях игроку приходится угадывать и он может проиграть, если ему не повезёт.

Что если мы добавим ещё одно правило? Когда у игры нет логичного пути вперёд, то мы можем попросить о помощи. Если ИИ соглашается, что игрок не может ничего поделать, то приходит ему на помощь. В противном случае игрок немедленно проигрывает. Это может быть интересным. Какой может быть такая помощь? Возможно, нужно открыть одну клетку, вне зависимости от наличия в ней мины:

Таким образом, мы полностью избавились от ситуаций, в которых можно было проиграть случайно.

Однако тут есть одно исключение: по-прежнему существует вероятность вырожденных ситуаций, в которых глобальный солвер не может закончить вычисления за разумный промежуток времени. К сожалению, это неизбежный результат того, что задача «Сапёра» NP-полная.

Как кнопка «Попросить помощи» влияет на игровой процесс? Она приводит тому, что игра больше сосредотачивается на логике; это самый «головоломный» вариант «Сапёра». Кто-то может подумать, что игра станет проще, но на самом деле она усложняется. Теперь ошибкам игрока нет оправданий, и кнопка накажет его, если он что-то упустил. Без кнопки легко прийти к выводу, что ты исчерпал все логичные возможности и единственный вариант развития событий — попытаться угадать случайным образом. Но из-за существования кнопки игрок обязан быть прав в этой оценке.

В заключение

Реализовав полный солвер «Сапёра», мы смогли создать разновидность игры, избавленной от её проклятья: теперь невозможно проиграть из-за того, что приходится выбирать случайно, когда уже почти решил всё поле. Эта версия отличается от оригинальной игры только в те моменты, когда нужно угадывать случайным образом, поэтому могу предположить, что она намного увлекательнее, чем оригинальная игра.

Кроме того, мы разработали вариант игры, автоматически решающий простые локальные правила. Стоит ли использовать такую помощь — зависит только от вас.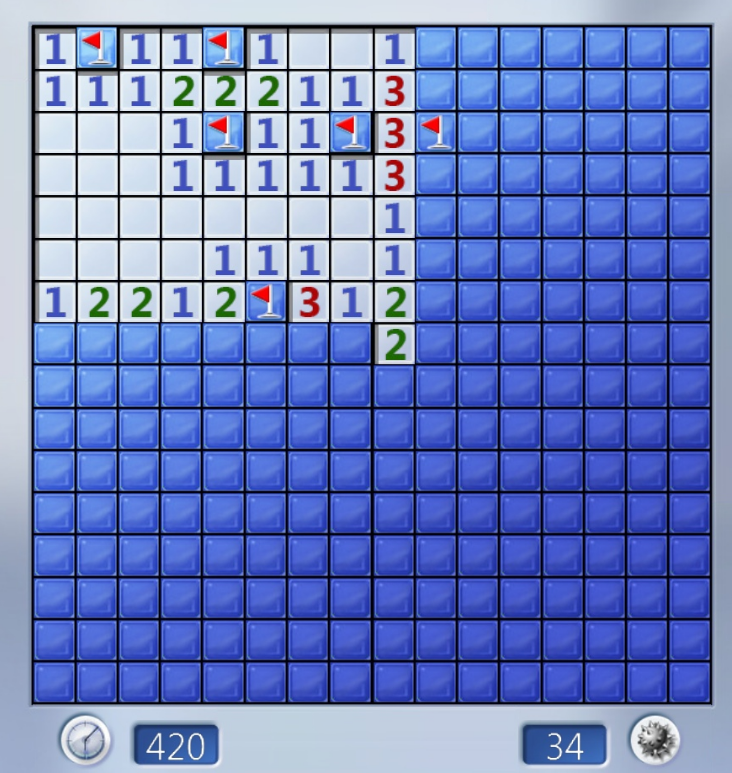 Она смещает фокус игры с механического щёлканья к более головоломному игровому процессу. При этом необязательно пользоваться усовершенствованием геймплея, которое обеспечивает кнопка «Попросить помощи».

Продвинутая тактика игры в «Сапёр» / Хабр

[Пятничный перевод статьи 1999 года одного из авторов движка игры Thief Шона Барретта]

Неприятное положение в «Сапёре»

В этом положении я знаю, что вокруг меня есть куча мин, но не могу определить, где они находятся. Несколько мин может быть в одном из двух мест (розовые или голубые), группа мин может быть расположена в одной из двух комбинаций (светло-/тёмно-зелёные). Кроме того, есть ещё сложная ситуация с «5» и «6» в левом верхнем углу, которую я никак не выделил.

Голубые/розовые — взаимоисключающие пары, светло-/тёмно-зелёные — взаимоисключающие группы

«Сапёр»: логика или вероятность

В «Сапёра» можно играть двумя способами: как в логическую или в вероятностную игру.

Технически, вероятность подразумевает логику. Если вы можете логически доказать, что мина должна находиться в определённом месте, то вероятность равна 100%. Если можете доказать, что её в этом месте нет, то вероятность равна 0%. То есть в каком-то смысле для нас важны только вероятности. Тем не менее, игрок для распознавания таких стопроцентных ситуаций игрок использует логическую дедукцию. Иногда, особенно на низких уровнях сложности, её достаточно для прохождения уровня, никакого подсчёта вероятностей не требуется.

Но бывают такие ситуации, когда вся логика мира не может вас спасти. Простой пример — ситуация с «T», которую видно внизу по центру. Она немного осложняется дополнительными соседними минами. (В простейшем случае «2» заменяется на «1», а «5» — на «3», чтобы ситуация была симметричной.)

Нет никакого способа получить больше информации о вероятном положении одной мины, оставшейся в одной из этих клеток. Шансы пятьдесят на пятьдесят — можете бросать монетку. Когда у вас получается что-то подобное, лучше сразу же сделать выбор и не откладывать на потом. Если догадка будет неверной, то вы хотя бы сэкономите время на решение остальной части поля. (Но лично я стремлюсь к завершённости, поэтому оставляю такие случаи на потом. И не вините себя за то, что не угадали. Когда победа или проигрыш зависят от броска монеты — это плохой гейм-дизайн.)

Тактика в конце игры

В эндшпиле можно использовать очень простую тактику — считать количество оставшихся мин. Допустим, я решил всё, кроме правой нижней части поля. Здесь может быть всего две конфигурации мин, соответствующих данным:

Возможные конфигурации мин в правом нижнем углу

Если у вас получилась такая позиция и счётчик говорит, что осталось всего две мины, то ответ готов: это должна быть конфигурация B.

Если счётчик говорит, что осталось три мины, то это необязательно конфигурация A. Это может быть схема B с оставшейся миной в одной из правых нижних групп клеток 3×3.

На самом деле, шансы в пользу конфигурации B.

Локальные вероятности

Если вы исследуете вероятности только «локально», вы видите, что каждая из клеток в отмеченных взаимоисключающих группах имеет шанс 50-50 быть миной. Говоря «локально», я подразумеваю, что если рядом с двумя неизвестными клетками есть «1», то вероятность спрятанной мины у каждой из них равна 50%.

Именно такая ситуация сложилась внизу в центре: каждая из соседних клеток, соседних к неизвестной паре, содержит в точности одну мину, то есть каждый из соседних фрагментов данных предполагает 50-процентную вероятность. В самом левом верхнем углу похожая ситуация:

С абсолютной точностью в каждом из розовых овалов есть по одной мине, то есть всего осталось 7 мин

Ситуация в правом нижнем углу тоже чем-то похожа: рядом с каждым из чисел на «границе» есть одна мина и две клетки, в которых она может быть.

Если рядом с клеткой есть одна скрытая мина, но три закрытых клетки, то вероятность мины в каждой из клеток составляет 33%; каждая из четырёх закрытых клеток имеет вероятность 25%. Если у нас две скрытые мины и три закрытых клетки, то каждая клетка имеет вероятность 66%.

Вот ситуация с «локальной вероятностью» для всего поля:

Как вы видите, несколько клеток в верхней левой области имеют несколько вероятностей; закрытая клетка рядом с «2» и «6» и одна рядом с «3» и «5». (Клетка рядом с «5» и «6» благодаря им всё равно имеет вероятность 66%, поэтому нет видимого несоответствия.)

Разрешение конфликтов локальной вероятности

Вы наверно, задаётесь вопросом, что значит наличие конфликтующих локальных вероятностей. Интуиция может подсказать, что наибольшая вероятность должна выиграть. Например, клетка между «6» и «2» должна на самом деле иметь 66%. Это будет значить, что у крайней левой клетки с вероятностью 50% она на самом деле равна 33%.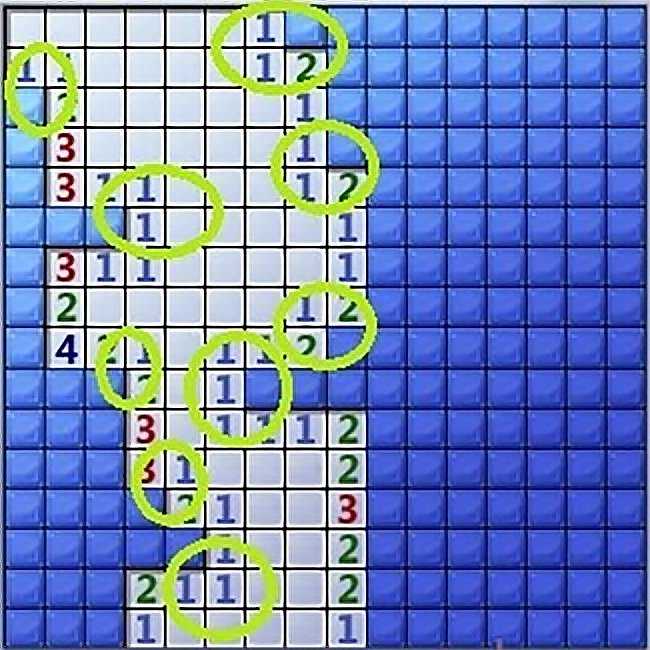 Или можно попробовать как-то комбинировать приоритеты: возможно, вероятность будет 5/6 или средним значением.

Но ничто из этого на самом деле неверно. Данные, из которых получены вероятности, не независимы друг от друга, поэтому никакие прямолинейные математические расчёты не будут верными. Причина правильности локальной догадки о 50% внизу в центре в том, что она действительно независима ни от чего другого. Если случайным образом воссоздавать поле по уже имеющимся у нас данным, то ровно в половине из моделей мина будет в одной из двух клеток. (Вероятность иногда запутывает людей, которые не могут разобраться, какие правила расчёта вероятностей применимы в конкретной ситуации. Такой подход — это гарантировано верный путь, потому что он основан на определении вероятности в статистическом прогнозировании: вычисление выполняется измерением во всех возможных конфигурациях, которые могли привести к текущей ситуации, при этом все они считаются одинаково вероятными.)

То есть для верных измерений в ситуации в левом верхнем углу нужно рассмотреть все возможные конфигурации мин, удовлетворяющие уже собранным данным, а затем посчитать, какой процент из них содержит мину в нужной позиции.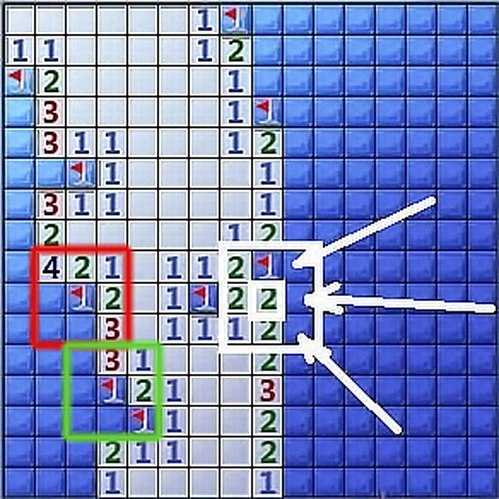

Непосредственный подсчёт потребовал бы много времени. К счастью, существуют и другие способы.

Подсчёт конфигураций

Абстрактный способ вычисления вероятностей заключается в обходе всех возможных конфигураций мин, отбрасывании конфигураций, не отвечающих собранным данным, и вычислении статистики для каждой из возможных позиций.

Более практичный подход — рассматривать только те варианты, которые нельзя отбросить. Для этого нам нужно применить логику и сгенерировать все возможные ситуации, которые могут соответствовать имеющимся данным. Я уже показывал два варианта для правого нижнего угла, а вот вероятности для левого верхнего:

Возможные конфигурации для левого верхнего угла

(Как и раньше, овал высотой в две клетки показывает, что мина может с одинаковой вероятностью находиться в любой из клеток. Я мог бы перечислить каждый из двух этих случаев отдельно, то есть получилось бы 10 конфигураций, но никакой пользы в этом для нас нет.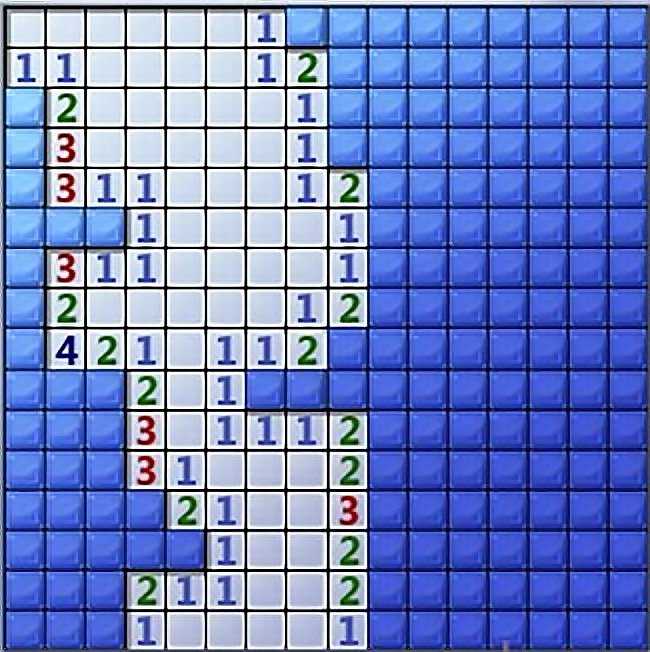 Структура таблицы: два ряда (пронумерованные как «1» и «2») отличаются положением мины в четвёртом ряду. Три столбца характеризуются положением мин во втором ряду.)

Теперь есть искушение воскликнуть: «ага, вот пять случаев, так что мы можем подсчитать количество случаев для каждой из возможных позиций мины». Например, мина находится в четвёртом ряду (рядом с левой нижней «1») находится слева в двух верхних случаях, и справа в трёх нижних случаях. Поэтому можно решить, что она имеет вероятность в 60% находиться справа, рядом с «6». (Это позиция с конфликтующими локальными вероятностями 50% и 66%.)

Однако мы упускаем одну тонкость — количество мин в некоторых случаях разное: в A1 шесть мин, в B2 — четыре, и по пять во всех остальных случаях.

Считаем ненайденные мины

Для подробного изучения этой тонкости давайте вернёмся к более простой ситуации в правом нижнем углу.

Возможные конфигурации с правом нижнем углу

Предположим, что я уже открыл остальное поле и знаю, что осталось ровно три мины.

Есть искушение предположить, что наиболее вероятна конфигурация A ровно с тремя минами. Но это неверно.

Ещё одно искушение — вспомнить, сколько всего было мин и сколько всего клеток, и сказать: «каковы шансы того, что нижняя область 3×3 будет пустой». Это тоже неверно. Очень сложно объяснить, почему это ошибка, наверно, её можно сравнить с парадоксом Монти Холла. Однако достаточно сказать, что в действительности шансы в этой ситуации не зависят от общего количества мин и размера поля.

Правильный ответ таков: сколько возможных конфигураций из трёх мин соответствуют нашим знаниям о поле? Из рисунка мы видим, что две: конфигурации A и B. Но в B всего две мины. Третья мина может быть в любой из клеток нижней области 3×3, о которой мы пока не собрали никаких данных. То есть всего есть девять вариантов конфигураций B, я просто не стал изображать их все.

Следовательно, существует всего десять возможных конфигураций. Каждая из десяти конфигураций равновероятна. (Как я упоминал ранее, это критически важно для понимания вероятности. Шансы того, что компьютер сгенерировал любой из этих вариантов малы, но они равно малы, потому что компьютер [насколько мы знаем] давал каждой конфигурации равные шансы. Вы с равной вероятностью можете выбросить конфигурацию из десяти «орлов» подряд и последовательность два «орла», одна «решка», один «орёл», три «решки», один «орёл», одна «решка» и один «орёл». Вероятнее выбросить в сумме пять «орлов» и пять «решек», но не никакую конкретную последовательность «орлов» и «решек». В «Сапёре» мы имеем дело с конфигурациями мин, которые похожи на последовательности бросков монеты.)

Поскольку каждая из десяти конфигураций (девять для B, одна для A) равновероятны, конфигурация B в данном случае имеет вероятность 90%!

Если бы на этом этапе было четыре мины, то у конфигурации A имелось бы девять вариантов. Конфигурация B имела бы по одному варианту для каждого варианта расположения двух мин в левом нижнем углу; это C(9,2), то есть 9!/((9-2)! * 2!) или 9*8/2, равное 36. В этом случае конфигурация B имела бы вероятность только 75%.

С пятью минами конфигурация A имела бы 36 вариантов, а конфигурация B — 9*8*7/6 = 84 варианта; то есть шансы B были бы чуть больше 66%.

В случае шести мин B имела бы вероятность 60%. С семью минами у B было бы всего 50%. С восемью минами B была бы менее вероятна, чем A; в этом случае с таким количеством мин в оставшихся позициях конфигураций становится меньше. Рассмотрим наихудший случай, когда осталось 11 мин. (Шанс этого чрезвычайно мал, но если такая ситуация возникнет, то применимы эти вероятности.) В конфигурации B, во всех закрытых клетках будут мины, в конфигурации A во всех, кроме одной. То есть существует 9 вариантов для A и всего один для B.

Окончательное решение

На имеющемся у нас поле осталось девять мин. Одна из них находится в центральной нижней области, и её положение полностью независимо, поэтому можно его игнорировать. То есть мы рассматриваем всё поле, кроме этого случая: не найдено всего восемь мин. (Чтобы не возникло путаницы, я продолжу явным образом считать овал в левом верхнем углу, потому что это изображение левого верхнего угла.)

Может сложиться любая комбинация из левой верхней и правой нижней конфигураций, за исключением одной из них (A1 + A), для которой потребуется девять мин. Поэтому мы должны перечислить каждую из этих возможных конфигураций и сосчитать оставшиеся мины и закрытые клетки.

На самом деле, количество закрытых клеток независимо: их девять в правом нижнем углу и три в левом верхнем, то есть всего 12.

Вверху слева	Внизу справа	Количество мин	Осталось мин	Закрытые варианты
A1	B	8	0	1
B1	A	8	0	1
B1	B	7	1	12
A2	A	8	0	1
A2	B	7	1	12
B2	A	7	1	12
B2	B	6	2	66
C2	A	8	0	1
C2	B	7	1	12

Таким образом, всего существует 118 возможных комбинаций. Исходя из этого мы можем независимо посчитать количество комбинаций для каждой из левых верхних и правых нижних конфигураций:

Конфигурация	Варианты	Процент
A1	1	1
B1	13	11
A2	13	11
B2	78	66
C2	13	11
A	15	13
B	103	87

Далее я обошёл каждую клетку на поле и вычислил её вероятность, суммировав количество вероятностей, в которых она появляется, и поделив на 118. (На самом деле, просто сложив указанные выше проценты.) Кроме того, в среднем в каждой из закрытых клеток есть мина в 15 из 118 вариантов (то есть шансы на то, что по крайней мере в одной закрытой клетке есть мина, очень высоки). [Это можно вычислить умножением количества оставшихся мин на закрытые варианты, что даёт нам среднее количество мин в закрытых клетках.]

Вероятности наличия мины

(Следует сказать, что это не показывает всей доступной информации. Например, мы знаем, что вероятности двух тёмно-зелёных клеток с 87% связаны — если одна верна, то другая тоже. И голубые 13-процентные клетки, в которых есть мины по конфигурации A, тоже связаны. Остальные голубые 13-процентные клетки не связаны. Если в одной из них есть мина, вероятность того, что в любой из оставшихся есть мина, уменьшаются.)

Играем в игру

Скорее всего, играя в «Сапёра», вы не захотите корпеть над всеми этими вычислениями.

И я тоже.

Но я действительно перечислил все возможные конфигурации в левом верхнем и правом нижнем углах. Я заметил, что в одной конфигурации (B2-B) используется на одну мину меньше, чем во всех остальных, и применил проверенное временем правило «меньше мин — значит, больше закрытых вариантов» (которое действует приблизительно пока количество закрытых клеток меньше чем удвоенное количество ненайденных мин). Это означает, что намного вероятнее конфигурации с меньшим количеством мин.

Поскольку в левом верхнем углу было множество конфигураций, определение шансов для любой клетки довольно сложно. Поэтому я просто выяснил, что конфигурация B в правом нижнем углу намного более вероятна, и случайно выбрал одну из подходящих клеток. (Я надеялся, что она позволит мне закончить правый нижний угол, а потом, вооружённый большей информацией о количестве оставшихся мин, я смогу завершить левый верхний угол, после чего мне придётся бросить монетку для выбора внизу в центре. Разумеется, в идеале нужно было выбрать клетку, максимизирующую вероятность получения полезной информации, но любая из этих догадок позволила бы мне «войти» в правый нижний угол для дальнейшего сбора данных.) Шансы были выше у конфигурации B, поэтому я выбрал клетку, в которой была мина в конфигурации A.

Восемь раз из девяти я был бы прав.

Sapper — Системные требования симулятора обезвреживания бомбы — Могу ли я запустить его?

Sapper — Defuse The Bomb Simulator Системные требования — полные спецификации, средство проверки системы и необходимые настройки игрового ПК.

Sapper — Минимальные требования симулятора бомбы обезвредить

• Память: 4 ГБ
• Видеокарта: NVIDIA GeForce GTX 970
• ЦП: Intel Core 2 Duo E8400
• Размер файла: Неизвестно
• ОС: Windows XP, Windows Vista, Windows 7, Windows 8, Windows 8.1, Windows 10

Сапер — Обезвредить The Bomb Simulator рекомендуемые характеристики

Неизвестные рекомендуемые системные требования

Можете запустить? Проверьте свой компьютер на соответствие системным требованиям Sapper — Defuse The Bomb Simulator .

Могу ли я запустить его?
Автоматическое тестирование ПК Могу ли я запустить его?
Введите информацию о вашей системе

Могу ли я запустить Sapper — Deuse The Bomb Simulator?

Чтобы играть в Sapper — Defuse The Bomb Simulator, вам потребуется как минимум процессор, эквивалентный Intel Core 2 Duo E8400. Самая дешевая видеокарта, на которой вы можете играть, — это NVIDIA GeForce GTX 970. Системные требования Sapper — Defuse The Bomb Simulator гласят, что вам потребуется не менее 4 ГБ оперативной памяти.

Sapper — Defuse The Bomb Simulator будет работать на ПК с Windows XP, Windows Vista, Windows 7, Windows 8, Windows 8.1, Windows 10 и выше.

Ищете обновление? Воспользуйтесь нашими простыми в использовании руководствами по настройке Sapper — обезвредить симулятор бомбы , чтобы найти лучшие и самые дешевые карты. Фильтр для Sapper — Сравнение видеокарт и процессоров Defuse The Bomb Simulator. Мы поможем вам найти лучшее предложение по правильному оборудованию для запуска игры.

Sapper — обезвредить симулятор бомбы FPS — какую частоту кадров вы можете ожидать?

Сколько FPS я получу в Sapper — Defuse The Bomb Simulator? Монитор FPS — это первый шаг к пониманию того, как компоненты вашего игрового ПК работают в реальных условиях. Это идеальный способ отслеживать Sapper — Defuse The Bomb Simulator FPS падает и заикается.

Загрузите наш бесплатный Монитор FPS через Overwolf, чтобы подсчитывать частоту кадров во время игры и проверять, как изменения ваших настроек могут повысить FPS и повысить производительность Sapper — Defuse The Bomb Simulator. Наше приложение совместимо с сотнями лучших компьютерных игр и уже доступно.

Скачать :	Через Steam
Разработчики :	Игры с живым движением Взрывной отряд
Издатели :	Ultimate Games S.A. Игровая фабрика SA Взрывной отряд
Категории :	Действие Приключение Моделирование
Сапер — обезвредить симулятор бомбы Дата выпуска :	23 января 2023
Сапер — Симулятор обезвреживания бомбы Цена сегодня:	$9,99

Что такое Sapper — Симулятор обезвреживания бомбы?

Узнайте все тонкости одной из самых опасных профессий в мире. Обыск, взлом, взлом, обезоруживание, работа под давлением. Добро пожаловать в типичный день Сапера. Храбрость закаляется в звуках тикающих бомб и в ощущении холодного пота на спине.

Ищете готовую систему? В нашей базе данных 165 портативных компьютеров, на которых можно запускать Sapper-Defuse The Bomb Simulator . Мы принимаем более 24 игровых ноутбуков стоимостью менее 1000 долларов. Ознакомьтесь с нашей полной таблицей сравнения ноутбуков, чтобы найти подходящие системы или лучшие предложения, которые мы выбрали ниже.

Последние сообщения

• Бесплатный монитор FPS для отслеживания частоты кадров в игре

  2 марта 2023 г.

класс = «маленький заголовок»>

Системные требования The Last of Us Системные требования Diablo 4 Системные требования ГТА 5 Наследие Хогвартса: системные требования Системные требования Valorant Системные требования Resident Evil 4 Remake Системные требования FIFA 23 Системные требования Fortnite Системные требования КС ГО Системные требования Elden Ring Системные требования Red Dead Redemption 2 Системные требования Call of Duty: Warzone 2 Сыновья леса системные требования Системные требования Майнкрафт Системные требования Apex Legends Системные требования Genshin Impact Системные требования Wo Long: Fallen Dynasty Системные требования Kerbal Space Program 2 Системные требования Dead Island 2 Системные требования The Sims 5

Как выиграть в Saper: советы и рекомендации

«Сапер» относится к числу стандартных игр Windows и отличается предельной простотой и незатейливостью исполнения. Жанр игры логический. Это увлекательная головоломка, которая заставляет думать, думать и быстро принимать правильные решения. Благодаря наличию нескольких уровней разной сложности может заинтересовать детей и взрослых.

Знакомство с игрой

При запуске «Сапера» на экране появляется картинка — коробка с ячейками. В зависимости от выбранного уровня поле может быть меньше или больше. В процессе игры необходимо открывать эти клетки, угадывая, что скрывается за каждой из них. Основных вариантов два — либо там мина, либо номер. Иногда встречаются пустые ячейки. Число в ячейке означает, сколько полей с минами примыкает к ней.

Логически рассуждая, игрок постепенно открывает клетки на поле одну за другой. Рассуждая, он определяет, где мины спрятаны, а где их нет. Мины отмечаются нажатием правой кнопки мыши (на месте мины появляется флажок), а ячейки, где они отсутствуют — слева. Как победить в игре «Сапер» на компьютере? Откройте все ячейки, правильно отметив содержимое каждой из них. Да, игра не предусматривает права на ошибку. Как только игрок делает неверный ход, игра заканчивается — все мины взрываются.

Когда игрок начинает открывать ячейки, запускается секундомер. Освоив принцип «Сапера», вы сможете на время начать играть, устанавливая все новые рекорды.

От простого к сложному

Наличие нескольких вариантов сложности дает возможность новичкам постепенно вникать в суть игры. Уровень Новичок представляет собой поле 9 х 9 клеток, на котором спрятано 10 мин. С него и стоит начать, ведь этот уровень сложности позволяет легче и комфортнее освоиться в игре. Узнав, как победить в «Сапере» на маленьком поле с малым количеством мин, можно двигаться дальше.

Даже те, кто считает себя умным и умным, не пренебрегают принципом от простого к сложному. Он поможет максимально быстро вникнуть в суть игры и показать первые результаты.

Советы: как победить в игре «Сапер»

1. Начало игры таково: игрок случайным образом открывает несколько ячеек. Очень хорошо, если получится попасть в пустое поле. При этом сразу открывается кусок с уже «угаданными» ячейками. Это упрощает дальнейшие размышления. Вы можете запускать игру несколько раз, чтобы открыть один или несколько таких сайтов.

2. Проще всего рассуждать с ячейками, где указана цифра. После нахождения этой уникальной шахты можно с уверенностью открывать все остальные клетки, соседние с ячейкой с номером 1 мин, на них не будет. Аналогично и с цифрой 2 — если к этой клетке уже примыкают две мины, остальные клетки помечаются как свободные.

3. Многие, отвечая на вопрос, как выиграть в Сапер, признаются, что им помогает расстановка на сомнительных ячейках вопросительных знаков. Если навести указатель мыши на ячейку и дважды щелкнуть по правой клавише, на ячейке появится вопросительный знак. Он может защитить игрока от поспешных решений. Позже на месте выпуска можно отметить мину или ее отсутствие.

4. Если в какой-то момент игры перед вами встанет выбор: открыть клетку наугад или оставить этот сайт «на потом», выбирайте второй вариант. Сложный кусок лучше отложить до того момента, когда в этой части поля откроется больше клеток, и принять решение будет проще.

Пробуя разные стратегии, придуманные другими людьми, каждый игрок постепенно вырабатывает собственные схемы и тактики. Это происходит путем многочисленных проб и ошибок. Но при должном упорстве игрок продемонстрирует на деле, как выиграть в Сапер на компьютере.

Почему иногда невозможно победить?

С этой проблемой, как правило, игроки не встречаются на двух простых уровнях. Но играя на двух сложных — профессиональных и специальных, игроки особенно часто задаются вопросом, как выиграть в Сапер, и возможно ли это? Дело в том, что в этих раундах часто возникают ситуации, когда приходится действовать наобум. Ситуация на игровом поле может сложиться так, что ни интеллект, ни разум, ни уловки не смогут помочь игроку. В этом случае приходится полагаться только на удачу. Если вам повезет и следующая ячейка будет открыта, игра продолжится.