Подсчет очков в преферансе: Расчет пули в преферансе | Страшно интересно!!!
Расчет пули в преферансе | Страшно интересно!!!
Привет, друзья!
Сегодня, как и обещал, рассмотрим расчет пули в преферансе, в процессе игры. Вот Вы сыграли игру Вам и вашим соперникам зачислили определенное количество очков. Сразу договоримся о какой системе игры идет речь. Рассматриваем вариант игры Сочинка. Распасы в игре не прогрессирующие, то есть 1, 2, 2, 2, … и т.д. Вист Джентельменский. Длина пули не важна. Итак начнем.
Подсчет очков в игре ведется кратно тому количеству очков, величину игры которой Вы играете. Например, играет шестерную игру, все очки насчитываются кратными 2. Играем семерную игру – 4, восьмерную – 6, девятерную – 8, десятерную – 10. Рассмотрим подсчет очков для шестерной игры.
Количество очков в пулю. За шестерную игру начисляется 2 очка в пулю. Эти очки будут засчитаны игроку, игравшему игру при условии, что он взял 6 или более взяток. Если взяток было заказано шесть, а взято меньше, то игрок получит очки в гору.
Висты. Каждому вистующему будет начисляться по 2 очка за каждую взятую взятку на игрока, играющего игру. Предположим, что игрок1 сыграл 6 пик, при этом игрок2 взял 2 взятки. Игроку2 на игрока 1 положено 4 виста, что и фиксируется в соответствующей графе бланка для записи.
Количество очков в гору. За каждую недовзятую взятку при шестерной игре игроку полагается 2 очка в гору. Причем это правило распространяется как на играющего игру, так и на вистующих игроков. Например, если игрок заказывал 6 пик, а взял при этом 7 взяток, то значит, кто-то из вистующих недобрал 1 взятку. Смотрим, у кого нет на руках двух взяток, тот и получает очки в гору. Второй при этом получает только висты.
Распасы. При распасах все достаточно просто. Считаем количество взятых взяток у каждого игрока, умножаем их на величину очков за взятку (одинарные или двойные распасы) и записывает данную величину в гору игрока. Например, в игре идет третий круг распасов (то есть уже двойные), игрок1 берет 3 взятки, игрок2 берет 2 взятки, игрок3 берет 5 взяток, соответственно игрок1 получит 6 очков в гору, игрок2 – 4, игрок3 – 10.
Для упрощения оконечных расчетов и поскольку это никак не повлияет на конечный результат рекомендуется следующая схема подсчета очков в гору при распасах. 1)Находим игрока у которого минимальное количество взяток (в нашем примере это игрок2 в 2 взятками) 2) Вычитаем минимальное количество взяток у оставшихся игроков 3) На оставшееся количество взяток у игроков начисляем очки в гору.
В нашем примере получим следующее: 1) У игрока2 всего 2 взятки 2) После вычитания у остальных игроков 2 взяток останется: Игрок1 – 1 взятка, Игрок 3 – 3 взятки. 3) По итогам записываем игроку1 – 2 в гору, игроку2 – 0 в гору, игроку3 – 6 в гору.
Если обратите внимание, то мы просто вычли у всех игроков по 4 очка в гору и все! Это нам существенно упростит расчет конечного результата.
Теперь отдельный случай, когда игрок «обламывается» и не играет заказанную игру, или, как говорят на карточном жаргоне, «остается без лап». В этом случае игроку за каждую недобранную взятку начисляют очки в гору.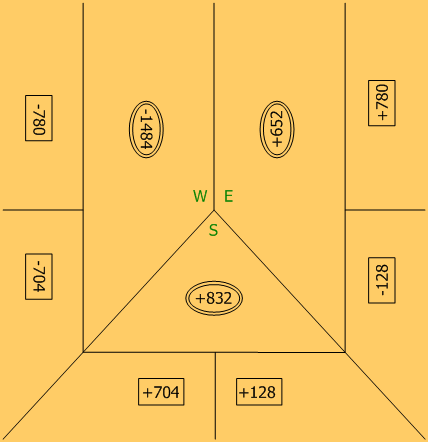 Пусть при шестерной игре он взял только 5 взяток, остался «без одной лапы». В этом случае ему засчитывается 2 очка в гору, никаких очков в пулю. Также вистующим товарищам, которые совершили это действо, начисляются дополнительные бонусы в виде дополнительных вистов. А именно, к числу набранных взяток вистующего добавляется еще одна взятка (которую недобрал играющий) и умножается на очки игры (в нашем примере на 2). Таким образом рассчитывается конечное количество вистов. Если, к примеру, один вистующий взял 5 взяток, а второй при этом пасовал или вистовал но взял 0 взяток, то висты рассчитываются следующим образом: первому достается (5+1)*2 = 12 вистов, а второму достается 2 виста «за облом». Соответственно, если игрок недобрал 2 взятку, то плюсуем эти две взятки каждому из вистующих.
Пусть при шестерной игре он взял только 5 взяток, остался «без одной лапы». В этом случае ему засчитывается 2 очка в гору, никаких очков в пулю. Также вистующим товарищам, которые совершили это действо, начисляются дополнительные бонусы в виде дополнительных вистов. А именно, к числу набранных взяток вистующего добавляется еще одна взятка (которую недобрал играющий) и умножается на очки игры (в нашем примере на 2). Таким образом рассчитывается конечное количество вистов. Если, к примеру, один вистующий взял 5 взяток, а второй при этом пасовал или вистовал но взял 0 взяток, то висты рассчитываются следующим образом: первому достается (5+1)*2 = 12 вистов, а второму достается 2 виста «за облом». Соответственно, если игрок недобрал 2 взятку, то плюсуем эти две взятки каждому из вистующих.
Для семерной игры расчет аналогичен, только каждая взятка ценится в 4 очка и в пулю, и в гору, и в вистах. Для восьмерной – 6, для девятерной – 8, для десятерной – 10, для мизера – 10.
При игре мизер, за каждую взятку играющего ему засчитывается 10 очков в гору. Если игра удалась, то играющему записывают 10 очков в пулю, а остальным ничего.
Если игра удалась, то играющему записывают 10 очков в пулю, а остальным ничего.
Вот таков расчет пули в преферансе, если у Вас возникли вопросы пишите на iigordanii@gmail.com
Удачи при игре!!!
На эту тему можно также почитать:
Метки: преферанс
Вы можете следить
за ответами к этой записи через RSS.
Расчет пули в преферансе
Расчет пули, применяемый на портале Мини-игры, подходит к тем видам преферанса, в которых 1 очко в пуле равно 1 очку в горе и 10 вистам. Значение пули в расчетах не участвует.
Ниже приведен пример пули после окончания партии, на примере которого мы рассчитаем результат игры для игроков А, Б, и В.
1. Определяем игрока с самой маленькой горкой (игрок А — 42 очка).
2.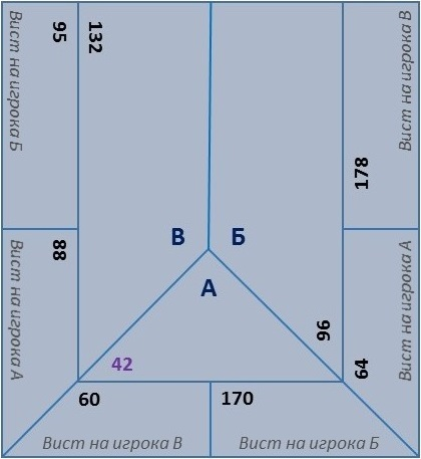 Вычитаем 42 очка из каждой горы. Получаем промежуточный результат:
Вычитаем 42 очка из каждой горы. Получаем промежуточный результат:
3. Теперь переведем для игроков Б и В полученное значение горки в висты.
Для игрока Б его гору 54 делим на 3 и умножаем на 10.
Получается 54 / 3 х 10 = 180.
Это будет “плюсовыми” вистами игроков А и В на игрока Б.
Повторяем такую же операцию для игрока В.
Получается 90 / 3 х 10 = 300.
Записываем игрокам А и Б по 300 вистов на игрока В.
Складываем висты игроков и получаем следующий промежуточный итог:
Теперь осталось лишь посчитать висты игроков друг на друга. Для этого вычитаем последовательно висты для каждой пары игроков:
Висты для игроков А и Б 350 — 64 = 286
Висты для игроков А и В 360 — 88 = 272
Висты для игроков В и Б 478 — 275 = 203
Записываем каждое значение со знаком “+” игроку, имеющему больше вистов, и со знаком “-”, соответственно, игроку с меньшим значением вистов. В итоге мы получаем промежуточный результат перед последним этапом подсчета:
В итоге мы получаем промежуточный результат перед последним этапом подсчета:
Теперь нам осталось лишь сложить значения вистов для каждого игрока. Так мы получим итоговую сумму выигрыша или проигрыша в вистах для каждого игрока.
Получаем финальный результат игры:
Правильность подсчета результатов очень легко проверить. Сумма вистов у всех игроков должна равняться 0.
В нашей реализации игры “Преферанс” игра ведется на заранее известную ставку, которую делают игроки. Соответственно, сумма проигрыша не может превысить сумму ставки, а сумма выигрыша — сумму общего банка. Конкретный размер выигрыша и проигрыша рассчитывается пропорционально количеству набранных вистов, которые мы с Вами научились считать выше.
Запись в преферансе и подсчет на троих. Правила игры в преферанс. Старые программы для игры в преферанс
Сегодня, как и обещал, рассмотрим расчет пули в преферансе. в процессе игры. Вот Вы сыграли игру Вам и вашим соперникам зачислили определенное количество очков. Сразу договоримся о какой системе игры идет речь. Рассматриваем вариант игры Сочинка. Распасы в игре не прогрессирующие, то есть 1, 2, 2, 2, … и т.д.
Сразу договоримся о какой системе игры идет речь. Рассматриваем вариант игры Сочинка. Распасы в игре не прогрессирующие, то есть 1, 2, 2, 2, … и т.д.
Подсчет очков в игре ведется кратно тому количеству очков, величину игры которой Вы играете. Например, играет шестерную игру, все очки насчитываются кратными 2. Играем семерную игру – 4, восьмерную – 6, девятерную – 8, десятерную – 10. Рассмотрим подсчет очков для шестерной игры.
Количество очков в пулю. За шестерную игру начисляется 2 очка в пулю. Эти очки будут засчитаны игроку, игравшему игру при условии, что он взял 6 или более взяток. Если взяток было заказано шесть, а взято меньше, то игрок получит очки в гору.
Висты. Каждому вистующему будет начисляться по 2 очка за каждую взятую взятку на игрока, играющего игру. Предположим, что игрок1 сыграл 6 пик, при этом игрок2 взял 2 взятки. Игроку2 на игрока 1 положено 4 виста, что и фиксируется в соответствующей графе бланка для записи.
Количество очков в гору. За каждую недовзятую взятку при шестерной игре игроку полагается 2 очка в гору. Причем это правило распространяется как на играющего игру, так и на вистующих игроков. Например, если игрок заказывал 6 пик, а взял при этом 7 взяток, то значит, кто-то из вистующих недобрал 1 взятку. Смотрим, у кого нет на руках двух взяток, тот и получает очки в гору. Второй при этом получает только висты.
Распасы. При распасах все достаточно просто. Считаем количество взятых взяток у каждого игрока, умножаем их на величину очков за взятку (одинарные или двойные распасы) и записывает данную величину в гору игрока. Например, в игре идет третий круг распасов (то есть уже двойные), игрок1 берет 3 взятки, игрок2 берет 2 взятки, игрок3 берет 5 взяток, соответственно игрок1 получит 6 очков в гору, игрок2 – 4, игрок3 – 10.
Для упрощения оконечных расчетов и поскольку это никак не повлияет на конечный результат рекомендуется следующая схема подсчета очков в гору при распасах.
В нашем примере получим следующее: 1) У игрока2 всего 2 взятки 2) После вычитания у остальных игроков 2 взяток останется: Игрок1 – 1 взятка, Игрок 3 – 3 взятки. 3) По итогам записываем игроку1 – 2 в гору, игроку2 – 0 в гору, игроку3 – 6 в гору.
Если обратите внимание, то мы просто вычли у всех игроков по 4 очка в гору и все! Это нам существенно упростит расчет конечного результата.
Теперь отдельный случай, когда игрок «обламывается» и не играет заказанную игру, или, как говорят на карточном жаргоне, «остается без лап». В этом случае игроку за каждую недобранную взятку начисляют очки в гору. Пусть при шестерной игре он взял только 5 взяток, остался «без одной лапы». В этом случае ему засчитывается 2 очка в гору, никаких очков в пулю. Также вистующим товарищам, которые совершили это действо, начисляются дополнительные бонусы в виде дополнительных вистов.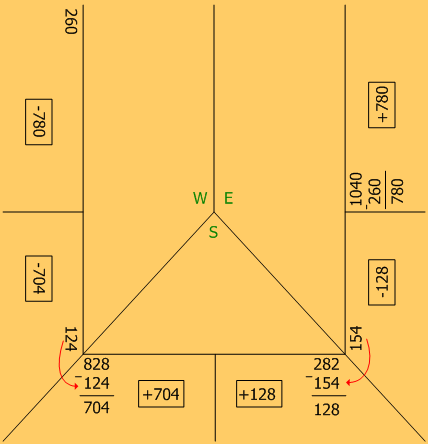
Для семерной игры расчет аналогичен, только каждая взятка ценится в 4 очка и в пулю, и в гору, и в вистах. Для восьмерной – 6, для девятерной – 8, для десятерной – 10, для мизера – 10.
При игре мизер. за каждую взятку играющего ему засчитывается 10 очков в гору. Если игра удалась, то играющему записывают 10 очков в пулю, а остальным ничего.
Вот таков расчет пули в преферансе. если у Вас возникли вопросы пишите на [email protected]
Приведены цены всех возможных контрактов.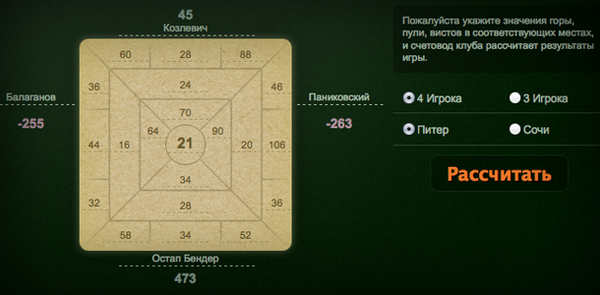 Т.е. каждой
игре соответствует некоторое количество очков, которое
игрок пишет в пульку при реализации контракта или в гору
— за каждую недобранную взятку при ремизе, а также на
висте за каждую взятую взятку. Однако цена контракта не
всегда отражает стоимость игры, т.е. баланс выигранных и
проигранных вистов. Между тем, каждая игра имеет свою
неизменную стоимость в вистах. Стоимость одной и той же
игры может быть различной в различных разновидностях
преферанса, но должна быть единой в пределах
длительности одной пульки. Все договорные правила,
признаваемые в отдельных компаниях, но нарушающие этот
принцип, должны быть, по возможности, пересмотрены.
Т.е. каждой
игре соответствует некоторое количество очков, которое
игрок пишет в пульку при реализации контракта или в гору
— за каждую недобранную взятку при ремизе, а также на
висте за каждую взятую взятку. Однако цена контракта не
всегда отражает стоимость игры, т.е. баланс выигранных и
проигранных вистов. Между тем, каждая игра имеет свою
неизменную стоимость в вистах. Стоимость одной и той же
игры может быть различной в различных разновидностях
преферанса, но должна быть единой в пределах
длительности одной пульки. Все договорные правила,
признаваемые в отдельных компаниях, но нарушающие этот
принцип, должны быть, по возможности, пересмотрены.
Пример: до окончания пульки осталось 2 очка. Игрок
сыграл девятерную. Он пишет в пулю недостающие 2 очка и
должен распорядиться оставшимися шестью очками. Их
следует списать с горы, даже, если запись в горе примет
отрицательное значение. Нарушение принципа неизменности
стоимости игры можно усмотреть в таких альтернативных
решениях:
а) оставшиеся очки пропадают;
б) оставшиеся очки записываются на остальных участников
игры вистами — скажем, на каждого из трех партнеров
пишется по 20 вистов. Неправильно! При расчете пульки 6
очков с горы будут стоить каждому не по 20, а по 15
вистов, так как гора делится на всех участников игры,
включая и ее «владельца»;
Неправильно! При расчете пульки 6
очков с горы будут стоить каждому не по 20, а по 15
вистов, так как гора делится на всех участников игры,
включая и ее «владельца»;
в) оставшиеся очки списываются с горы при игре в
гусарика с
неделимой горой. С горы следует списать лишь половину
«не поместившихся в пулю» очков.
4.1.2. При использовании повышающих коэффициентов в игре
(темные, бомбы, рефеты, елочки и т.п.) стоимость
сыгранной (как и не сыгранной) игры возрастает
пропорционально коэффициенту. Таким же непредсказуемым
образом возрастает стоимость игры при игре с призами
(так называемыми «скачками») — за то, что первым закрыл
пулю и т.д. При проведении квалификационных турниров
следует избегать разновидностей, предусматривающих такие
коэффициенты и скачкообразные изменения стоимости игр
(71).
4.1.3. Окончательный счет в сыгранной пульке
определяется в вистах. При проведении турниров критерием
победы является наибольшая сумма набранных вистов.
Организаторы могут, безусловно, вводить любые другие
критерии, как то: наибольшее количество выигранных
распасовок или минимальное совокупное количество взяток
на всех распасовках, наименьшее количество ремизов или
взяток на мизерах и т.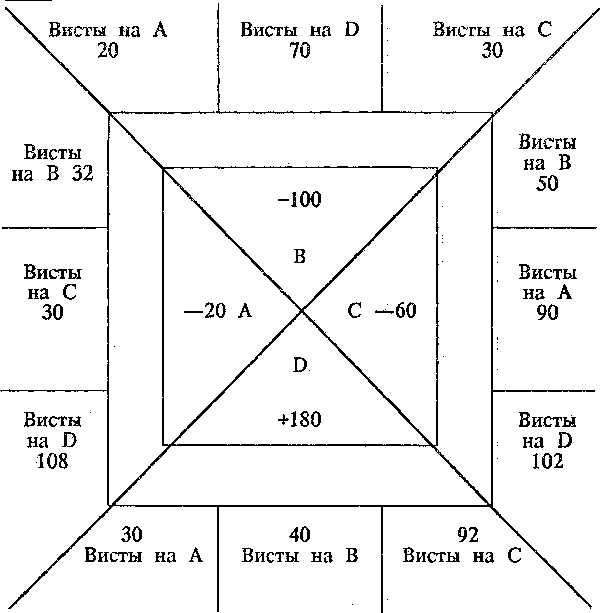 п., но определяющей и главной
должна быть разница в вистах.
п., но определяющей и главной
должна быть разница в вистах.
4.2. Игровая запись (пулька)
4.2.1. Результат каждой игры
заносится в игровой протокол, расчерченный традиционным
образом и известный как «пулька». Место для записей
результатов игр должно иметь 3 графы:
— горка для записи ремизов;
— пулька для записи сыгранных контрактов;
— вистовые записи (графа разделена на две или три
секции, соответствующих количеству остальных игроков).
За сыгранный контракт его цена (см. правило
2.2.2.)
пишется в графу «пулька». За несыгранный контракт
(ремиз) запись делается в «гору» — цена контракта
умножается на количество недобранных взяток. Вистующие
пишут за свои взятки в графе «висты», в той ее части,
которая относится к разыгрывающему. В случае ремиза
вистующих (недобора до обязательного количества взяток),
вистующие пишут в гору цену контракта, помноженную на
каждую недобранную взятку.
4.2.2. Величина игры и ставки являются предметом
предварительной договоренности между игроками. Играют до
определенного числа очков в графе «пулька». Например,
пулька до 50 очков.
Играют до
определенного числа очков в графе «пулька». Например,
пулька до 50 очков.
4.2.3. Каждый игрок пишет за сыгранные контракты в графе
«пулька» нарастающим итогом до тех пор, пока сумма его
очков не достигнет условленной, например, 50-ти. После
этого он «помогает» тому из противников, чья запись в
пульке больше. За каждое очко, записанное противнику «в
помощь», игрок пишет на него 10 очков в графе «висты».
Если у двух противников запись в пульке одинакова, то
помогают тому, кто сидит слева (72). Если игроки сообща
решили прекратить игру, каждый пишет на гору
недоигранное до условленного количество очков (это можно
сделать только при согласии всех участников игры). Как
только запись в пульке у всех игроков достигнет
условленной, игра окончена.
4.2.3.1. Для оказания помощи несущественно, что игрок,
которому адресована помощь, вистовал и поставил в гору
ремиз либо сидел на прикупе и в игре не участвовал.
4.2.3.2. Независтованные контракты, равно как и
завистованные, не списываются с горы, а записываются
исключительно в графу «пулька» — либо самому
разыгрывающему, либо тому игроку, которому, по условиям
игры, предназначается помощь.
4.2.3.3. В «ленинградской» разновидности преферанса («ленинградке»)
«помощи» нет, переигранные очки при расчете списываются
с горы вдвойне, а недоигранные очки выносятся на гору —
также вдвойне.
Пример: Играют втроем пульку до 50-ти. Один из игроков,
имея в пуле 48, сыграл восьмерную. Он делает полную
запись в пулю — 54. Игра происходит до тех пор, пока
суммарная запись в графе «пуля» у всех игроков станет
равной или превзойдет 150. В этот момент пулька
считается сыгранной и при расчете сыгранные сверх
необходимых 50-ти очки списываются с горы вдвойне, а
недоигранные до 50-ти — выносятся вдвойне на гору.
Допустим, в рассматривамый нами момент у всех троих было
в пуле 48. После сыгранной восьмерной игра закончилась:
у двоих осталось в пуле по 48, а у третьего стало 54.
Этот последний списывает с горы 8 очков, а двое его
партнеров приписывают по 4. Если суммарная величина
записей всех игроков превзошла 150, это ничего не
меняет: результат любой игры пишется полностью. То есть,
если бы вместо восьмерной была сыграна девятерная, то в
пулю была бы сделана запись 56, а с горы при расчете
списано 12 очков. Дальнейший расчет — как во всех
остальных разновидностях преферанса.
То есть,
если бы вместо восьмерной была сыграна девятерная, то в
пулю была бы сделана запись 56, а с горы при расчете
списано 12 очков. Дальнейший расчет — как во всех
остальных разновидностях преферанса.
4.2.4. Каждый игрок сам ведет запись результатов своей
игры.
4.2.5. Запись в каждой графе ведется нарастающим итогом
(правило 2.2.3.), чтобы обеспечить максимальную наглядность
при сравнении результатов. Писать следует разборчиво.
Цифры должны быть направлены своим основанием к
записывающему.
4.2.6. Запись следует делать немедленно после окончания
сдачи (75).
4.2.7. Ошибка в записи может быть поправлена партнерами,
но безнаказанно — только в первый раз, в виде
предупреждения. Общее правило наказания за неправильную
запись соответствует римскому праву (76) (за равное —
равным) и выглядит так: штраф за приписку должен
равняться величине приписки.
Примеры:
а) Если Вы записали на партнера вистов больше, чем
следовало, а партнер Вас поправил, Вам нужно списать
лишние висты, а партнер может написать на Вас столько,
сколько Вы на него незаслуженно приписали. Правила
хорошего тона предписывают Вам самому предложить
партнеру сделать это.
Правила
хорошего тона предписывают Вам самому предложить
партнеру сделать это.
б) Если игрок приписал себе лишние очки в пулю, то
столько же очков (в виде штрафа) он должен написать в
гору (исправив, разумеется, запись в пуле).
4.2.8. Правило карандаша. Ошибка считается сделанной и
требующей наказания в тот момент, когда записывающий
положил карандаш (77). Если записывающий игрок сам
заметил ошибку или ему на нее указали в тот момент,
когда ручка или карандаш все еще находятся у него в
руках, он может исправить запись без наказания.
4.2.9. Указать на ошибку в записи и внести исправления в
запись можно лишь до момента заказа следующей игры.
Окончание торговли в следующей сдаче является той
чертой, после которой сделанная запись, даже заведомо
ошибочная, может быть исправлена только по доброй воле
записывавшего.
4.2.10. Не сделанная вовремя запись (забытая) может быть
сделана не позднее окончания торговли в следующей сдаче.
Все увещевания забывшего записать свою игру или свои
висты должны быть прекращены в случае отказа хотя бы
одного из партнеров «вспомнить» предыдущую игру.
4.2.11. Для турниров по преферансу организаторам следует
подготовить пульки (турнирные листы или протоколы), на
которых поле записи содержит специальную графу с
указанием заказанной игры и ее результатов. Например:
6♠/ровно; или 8
/без
одной.
При наличии такой графы легче разбирать возможные споры
и конфликты, так как игра более четко документирована.
4.2.12. Если при окончательном расчете пульки возникают
дробные части итоговых сумм, то (во избежание округления
и возможного в связи с этим несхождения результатов)
одному из игроков добавляют или списывают с горы одно
очко, чтобы деление шло без остатка. Остальные участники
компенсируют эту запись вистами (пропорционально
количеству участников).
Пример: при игре втроем для удобства деления горы на 3
одному из участников с горы списали единичку. Двое
других пишут на этого игрока по 3 виста, теряя на этой
операции по 0,33 виста каждый.
4.2.13. Величина денежных ставок (если игроки условились
ввести такой дисциплинирующий фактор как денежная
ставка) устанавливается до начала игры.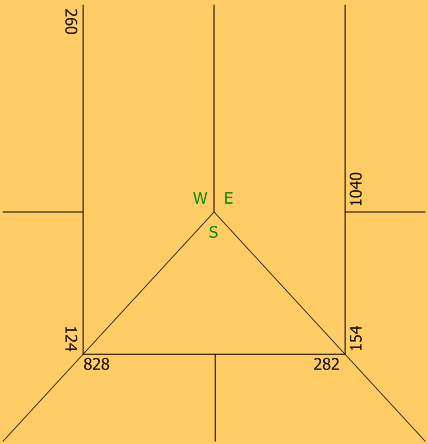 Выигранный вист
приравнивается определенной денежной сумме. После
расчета пульки количество выигранных или проигранных
каждым игроком вистом умножается на величину ставки.
Произведение является суммой выигрыша и проигрыша.
Выигранный вист
приравнивается определенной денежной сумме. После
расчета пульки количество выигранных или проигранных
каждым игроком вистом умножается на величину ставки.
Произведение является суммой выигрыша и проигрыша.
4.2.14. После того, как запись в графе «пулька» каждого
игрока достигла условленной перед игрой величины, пулька
считается законченной, т.е. сыгранной. Окончательный
расчет пульки может быть произведен одним из двух
равноценных способов:
Вариант 1.
Поскольку количество очков в пуле у всех игроков равно,
то эта графа не учитывается. Для удобства счета все
записи в горе подлежат «амнистии». Это значит, что
игрок, имеющий самую маленькую гору, списывает ее до
нуля, а все остальные игроки уменьшают свои горы на ту
же величину. От этой операции никто не теряет, но
считать чисто арифметически становится проще. Гора
каждого игрока умножается на 10 и делится на количество
участников игры, включая и самого хозяина горы. Если
деление без остатка невозможно, то поступают в
соответствии с правилом 4.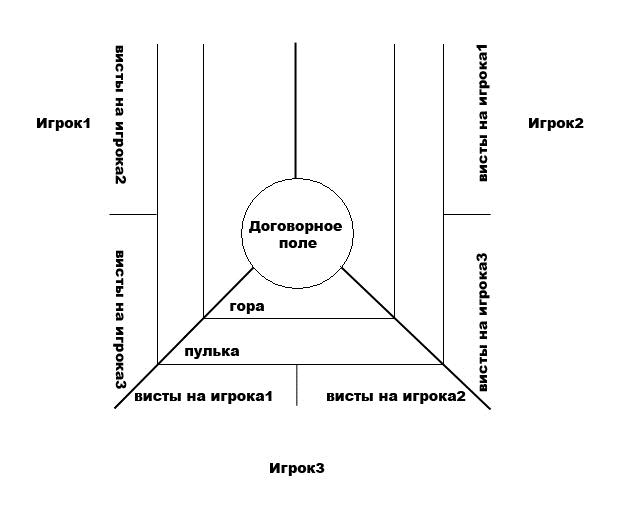 2.12. Частное от этого деления
является проигрышем хозяина горы каждому игроку в
отдельности и прибавляется к записям вистов на него
всеми остальными игроками. Так поступают с каждой горой,
а потом сравнивают количество вистов, записанных каждым
друг на друга. Итоговый выигрыш, разумеется, должен
равняться итоговому проигрышу, так как преферанс
относится к играм с нулевым результатом, то есть
проигрыш одних равняется выигрышу других.
2.12. Частное от этого деления
является проигрышем хозяина горы каждому игроку в
отдельности и прибавляется к записям вистов на него
всеми остальными игроками. Так поступают с каждой горой,
а потом сравнивают количество вистов, записанных каждым
друг на друга. Итоговый выигрыш, разумеется, должен
равняться итоговому проигрышу, так как преферанс
относится к играм с нулевым результатом, то есть
проигрыш одних равняется выигрышу других.
Вариант 2.
Второй способ незначительно отличается от первого одним
упрощением: вместо того, чтобы делить гору каждого
игрока на количество участников и всем писать висты друг
на друга, считают среднюю гору. Для этого складывают все
записи в горе и делят на количество участников. Если
деление без остатка невозможно, то поступают, как и в
предыдущем случае, в соответствии с правилом 4.2.12.
Полученное частное представляет средний проигрыш с горы
одного игрока. Если гора определенного игрока меньше
средней, то разницу умножают на 10 и пишут ему в графу
«выигрыш», а если гора больше средней, то разницу
умножают на 10 и ставят перед ней знак «минус». По
смыслу то же самое, а считать проще. Все вистовые записи
точно так же сравниваются между собой, а к итоговой
сумме добавляют выигрыш или проигрыш с горы. Сумма
выигрышей и проигрышей при проверке должна быть равной
нулю.
По
смыслу то же самое, а считать проще. Все вистовые записи
точно так же сравниваются между собой, а к итоговой
сумме добавляют выигрыш или проигрыш с горы. Сумма
выигрышей и проигрышей при проверке должна быть равной
нулю.
4.2.15. Закончить игру можно лишь по окончании пульки.
Досрочно прекратить игру можно лишь в чрезвычайных
обстоятельствах, выполнив все предусмотренные на этот
случай процедуры.
4.2.16. В случае замеченных нарушений Кодекса Преферанса
или Правил Проведения Турниров участник игры обязан
доложить о них организаторам турнира или в судейскую
коллегию. В спорных случаях решение по предполагаемым
нарушениями принимается квалифицированными арбитрами на
основе существующих правил и положений. Апелляция на
решения арбитров принимается по окончании турниров и
рассматриваются судейской коллегией.
Сноски
71. Такие «местные» правила будем
рассматривать как привносящие в преферанс нездоровый (и
несвойственный ему) элемент азарта и склоняющий чашу
весов не в пользу мудрости, трезвости, расчета и опыта,
а в пользу везения и риска.
72. Вопрос «кому помогать?» не заслуживает того
внимания, которое уделяют ему многие игроки. На самом
деле, это совершенно не важно, потому что никак не
влияет на экономический результат игры, так как каждый
сыгранный в процессе пули контракт одинаков по
стоимости, независимо от того себе или в помощь другим
пошла запись за этот контракт.
73. Во многих компаниях распространено договорное
правило, согласно которому нельзя помогать тому, кто
недобрал взяток на висте и сделал запись в гору, а также
тому, кто недобрал взяток на висте и сделал запись в
гору, а также тому, кто является сдатчиком в данной
раздаче и не принимал участия в игре. Мотивируется это
правило тем, что человек уже и так пострадал в этой
сдаче и не следует наказывать его дважды. Поскольку все
контракты одного уровня, сыгранные в процессе пульки,
одинаковы по стоимости, и адрес записи никак не влияет
на экономический результат, то есть посыл о
дополнительном наказании ложен, то данное правило может
привести единственно к увеличению продолжительности
пульки, так как возможны ситуации, когда результат одной
или нескольких игр будет списан с горы. Поэтому
применение указанного правила совершенно недопустимо при
проведении квалификационных турниров и нежелательно в
обычной игре.
Поэтому
применение указанного правила совершенно недопустимо при
проведении квалификационных турниров и нежелательно в
обычной игре.
74. В некоторых компаниях применяется правило, согласно
которому независтованные контракты (игры) разрешается
списывать с горы по желанию разыгрывающего. Это правило
фактически позволяет игроку изменять величину пули,
поэтому его нельзя применять при проведении
квалификационных турниров. В обычной же игре увеличить
пульку (или сыграть новую) можно с общего согласия всех
участников. Отдавать кому бы то ни было единоличное
право увеличивать заранее определенную продолжительность
игры было бы несправедливо.
75. Все советы партнеров, типа «сначала общественное —
потом личное», следует воспринимать с юмором, так как
запись является делом именно общественным.
76. Как и декларировалось в Преамбуле к Кодексу.
77. Именно поэтому правило называется «правилом
карандаша».
Теория. Стоимость игр и ремизов
Как определить стоимость в вистах игры или ремиза?
Для этого применяется первое ФУНДАМЕНТАЛЬНОЕ положение преферанса.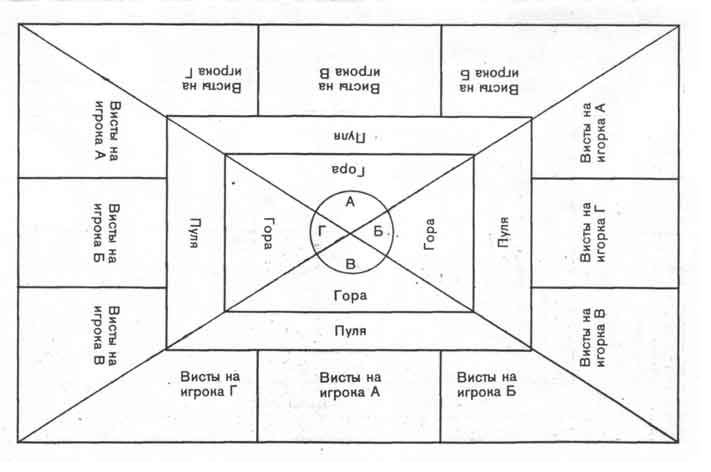
I. В современном преферансе расчеты между игроками производятся ТОЛЬКО ПОСЛЕ расписывания пули .
Этим, кстати, преферанс отличается, скажем от блэк-джека, секи или покера, где расчет производится после розыгрыша каждой раздачи.
В процессе игры ЗАПИСЫВАЮТСЯ ТРИ ВИДА условных единиц: висты, очки в пуле и очки в горе. Их стоимости РАЗЛИЧНЫ и оговорены в преферансной КОНВЕНЦИИ.
Наиболее распространены следующие соотношения между этими единицами: очки в пуле РАВНЫ очкам в горе и каждое очко в горе соответствует 10 вистам. Это конвенции обычных, без «изощрений» сочинки, ростова и классики. А в ленинградке одно очко в пуле приравнено к ДВУМ ОЧКАМ на горе. Каждое очко на горе — пока, по-прежнему, 10 вистов.
Значительно реже встречаются ДРУГИЕ соотношения (например в «камчатке»).
Как же расписывают оконченную пулю? Рассмотрим ПРИМЕР.
Сыграны игры. Все графы заполнены. В пуле у всех вместе сумма, равная двумстам или чуть больше, в зависимости от того, какая игра сыграна последней. Для удобства возьмем конечные цифры игроков. Существует несколько способов подсчета, но приведем только один, наиболее распространенный. Этот способ условно называется «4 кружочка». Расчет проводится в 6 этапов. Не пугайтесь! Весь расчет обычно занимает не более 3-х минут. Как раздачу разыграть. Не дольше.
Для удобства возьмем конечные цифры игроков. Существует несколько способов подсчета, но приведем только один, наиболее распространенный. Этот способ условно называется «4 кружочка». Расчет проводится в 6 этапов. Не пугайтесь! Весь расчет обычно занимает не более 3-х минут. Как раздачу разыграть. Не дольше.
1. Подсчет горок (вынос пули на гору или выравнивание пуль)
После окончания игры для определения победителя необходимо все разделы — пулю, горку и висты привести к одной единице — висту. Вист — конечная единица расчета между игроками. Одно очко в пуле равно двум очкам в горе, а одно очко в горе равно десяти вистам.
Переигравший в пуле свыше пятидесяти отнимает от сыгранного им пятьдесят. Разницу умножает на два и вычитает от своей горки. У кого недоиграно до пятидесяти, то разницу между своей пулей и пятьюдесятью он умножает на два и прибавляет к своей горе. Умножение на два — основное отличие ленинградки от других видов преферанса.
Получаем:
1 — переиграл 28 на 2 = 56, отнимаем, итог — 22 в горе ;
2 — переиграл 24 на 2 = 48, долой с горы, итог 12 ;
3 — недоиграл 18 на 2 = 36, прибавляем и в горе стало 70 очков ;
4 — недоиграл 28 на 2 = 56, плюсуем с горой и получаем 132 очка
.
каждый записывает полученное число за последней записью в своей горке и подчеркивает.
2. Амнистия
Амнистером по горе стал игрок под номером 2. После выравнивания пуль у него самая меньшая гора из всех, равная 12 очкам. Все вычитают из своих горок 12, записывают получившееся число, рядом с последней (подчеркнутой) записью и подчеркивают ее двойной чертой. В нашем примере получится:
1 — 10 очков ;
2 — 0 очков ;
3 — 58 очков ;
4 — 120 очков .
3. Средняя горка
Складываем амнистированные горки:
10+0+58+120=188
Делим на количество игроков, т.е. на четыре.
188:4=47 . Это «средняя горка».
4. Своя горка
Уже очевидно, что амнистер выиграл с горки +470 вистов. Остальные игроки вычитают из средней горки (47), свои числа, подчеркнутые двойной чертой, умножают получившееся значение на 10 и записывают результат с плюсом или минусом, обводя его первым кружочком. Ясно, что сумма чисел в первых кружочках у всех игроков равна нулю.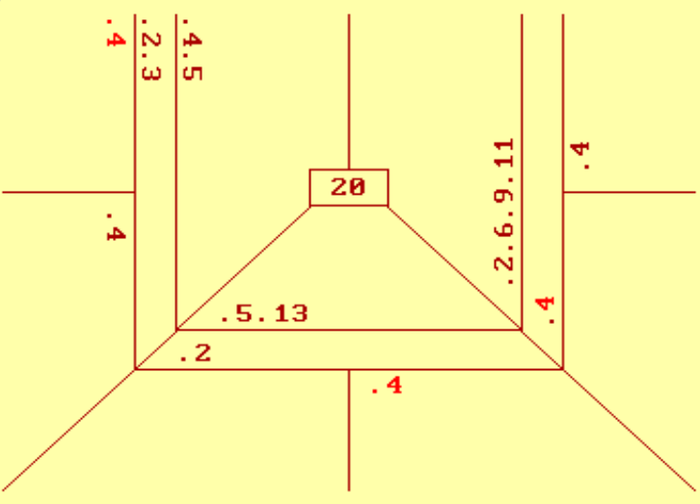 В нашем примере получится:
В нашем примере получится:
1.+470-100 =+370
2.+470-0 =+470
3.+470-580=-110
4.+470-1200 =-730
5. Подсчет вистов друг на друга
Каждый игрок считает разницу вистов друг с другом. Если у игрока больше вистов, то разница пишется с плюсом, меньше — с минусом. Эти три разности каждый игрок обводит в еще 3 кружочка, чтобы выделить из общего потока чисел и цифр. Ясно, что сумма всех 12 чисел в этих новых 12 кружочках (по 3 у каждого) также равна нулю.
6. Окончательный итог
Каждый игрок складывает числа в своих 4-х кружках и получает общую сумму выигрыша или проигрыша, выраженную в вистах. Эту сумму он обводит двойным кружком. Ясно, что алгебраическая сумма чисел в двойных кружках равна нулю. Пора приступать к расчету! Ведь преферанс — игра коммерческая.
Обычно среднюю горку, как самый заинтересованный, подсчитывает амнистер и оглашает всем цифру. В случае значительных расхождений в итоге часто пересчитывается именно она.
А как же определить стоимость отдельно взятой игры или ремиза?
Для этого применяется второе ФУНДАМЕНТАЛЬНОЕ положение.
II. В преферансе стоимости игр и ремизов в течение всей пули ПОСТОЯННЫ.
Имеется в виду, что стоимость, скажем, шестерной игры не зависит от номера раздачи в пуле и является величиной постоянной.
Применяя оба этих положения можно легко определить стоимость любой игры или ремиза.
Пример 1. Определение стоимости шестерной игры.
В лениградке втроем для закрытия пули 20
(игра идет до 60
по сумме трех пуль) нужно сыграть 30
шестериков. Допустим, что их все сыграл один игрок, записав в пулю 60
. Кроме этого, допустим, что, по окончании пули, у всех игроков на горе было по 80
очков. Игравший шестерики умножит свой «перебор» в пуле (40)
на 2, спишет с горы 80
и будет иметь нулевую гору. Его партнеры вынесут на гору по 40
и их горы станут по 120
. Средняя гора 2*120/3=80=800 вистов
. Это выигрыш с горы игравшего. Но на него записано по 16 вистов
за каждый из 30
шестериков. Всего 16*30=480
вистов. Итого, сыгравший 30
шестериков выиграет 800-480=320 вистов
. Значит стоимость ОДНОГО выигранного вистованного шестерика составляет 320/30=10,6 виста
.
Но на него записано по 16 вистов
за каждый из 30
шестериков. Всего 16*30=480
вистов. Итого, сыгравший 30
шестериков выиграет 800-480=320 вистов
. Значит стоимость ОДНОГО выигранного вистованного шестерика составляет 320/30=10,6 виста
.
Пример 2. То же, но сочинка. Там на гору не выносят — там «помогают». Поэтому считать несколько проще. В такой же пуле тоже нужно сыграть 30 шестериков. Сыгравший их закроет свою пулю и «поможет» партнерам на 40 в пулю — на 400 вистов . А на него запишут 8*30=240 вистов . Всего он выиграет 160 вистов . Значит в сочинке втроем шестерик стоит 160/30=5,3 виста . Ровно вдвое меньше, чем в ленинградке. Что, впрочем, было известно с самого начала.
Пример 3. Стоимость девятерика. Ленинградка вчетвером.
Хитрый приемчик! В сочинке вчетвером в пуле до 2 сыгравший 9, поможет на 60 вистов и пуля закончится. На него запишут 8 вистов . Всего — 52 виста . Значит в ленинградке девятерик стоит 104 виста .
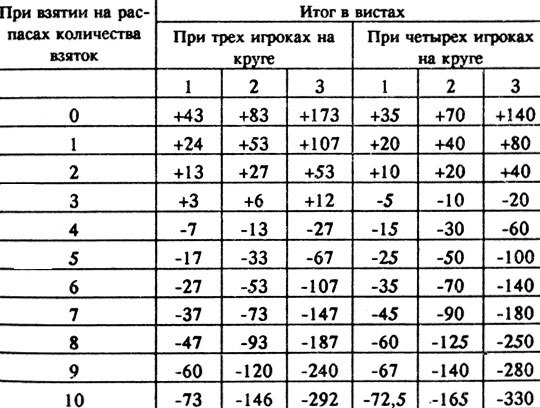
Пример 4. Определение стоимости ремиза. Сочинка вчетвером.
Сочинка вчетвером.
Вот, допустим, окончена пуля. И у всех все записи одинаковые. И тут играется еще 1 «сверхплановый» шестерик. Который выходит «без 1». Это на гору 2 очка. С горы придется раздать каждому партнеру по 5 вистов , всего 15 . И вистов записали вистующие 6 и 8 , а сдающий — еще 2 . Всего 31 вист . Именно столько составляет проигрыш шестерика «без 1» в сочинке вчетвером. А в ленинградке — 62 виста .
Потому больше ровно вдвое, что мало было жуликам. По «бандитской» питерской конвенции, при одинаковой денежной ставке за вист, все игры и ремизы дороже сочинских вдвое…
Привет, друзья!
Пришла пора научиться рассчитывать итоговый результат пули в преферансе . Посидели с друзьями, поиграли, завершили игру, а что же делать дальше, как посчитать результат? Именно ответу на данный вопрос и посвящена статья, чтобы в дальнейшем Вы не сталкивались с трудностями при расчете пули в преферансе. Также проведу вычисления на примере реальной пули , которую играл сам. К расчету берется вариант игры Питер на 4 человека до 21. Но это Вы сейчас увидите и из расписанной пули. Итак берем Пулю со следующими значениями (см. рисунок).
К расчету берется вариант игры Питер на 4 человека до 21. Но это Вы сейчас увидите и из расписанной пули. Итак берем Пулю со следующими значениями (см. рисунок).
1) Первое, что необходимо сделать — пересчитать разность пули у каждого игрока и перевести его в гору. Так как начальная величина пули составляет 21, а игроки закрыли свои пули на разное количество очков, то приведем пули всех игроков к единой величине 21. Для этого, у игроков величина пули которых превышает 21, вычисляем разницу между их пулей и 21, полученную величину умножаем на 2 и полученное число вычитаем из величины Горы.
Для игроков, величина пули которых меньше 21, также вычисляем разницу между 21 и их пулей, полученное число умножаем на 2 и полученную величину прибавляем к горе игрока. Проведем расчет для приведенного примера.
Игрок1. Пуля 56. Разница 56-21=35. Умножаем на 2: 35х2=70. Вычитаем полученную цифру из величины горы: Гора 76-70=6.
Игрок2: Пуля 12. Рассуждая аналогично получаем: (21-12)х2=18. Добавляем 18 очков в гору: Гора 40+18 = 58.
Добавляем 18 очков в гору: Гора 40+18 = 58.
Аналогично для Игрока3 находим: Гора 52+30 = 82.
Игрок4. Гора 80+10=90.
2) Следующим шагом находим игрока, у которого самая маленькая величина горы. В нашем случае это получился игрок1 с горой в 6 очков. Вычитаем данную величину у остальных игроков. Тогда получим следующие горы игроков: Игрок1=0, Игрок2=52, Игрок3=76, Игрок4=84.
3) Третим шагом суммируем горы всех игроков: 52+76+84=212, и делим на количество игроков: 212:4=53 и в заключение умножим на 10. Таким образом получим, что каждому игроку достается по 530 вистов. Теперь начинаем учитывать разницу между 530 вистами и очками горы каждого игрока. Каждое очко горы игрока отнимает 10 вистов. В итоге для игрока1: +530 вистов, для игрока2: 530-520=+10 вистов, для игрока3: 530-760=-230 вистов, для игрока4: 530-840=-310 очков. Теперь обязательно проверить, чтобы сумма положительных очков в горе была равна сумме отрицательных очков в горе. У нас +530+10=540, -230-310=-540. Отлично суммы положительных и отрицательных очков равны. Очки за Гору и Пулю посчитаны, львиная доля расчетов позади. Количество вистов каждого игрока за гору обычно записывается под именем игрока и обводится в круг или овал. Должно получится следующее:
Очки за Гору и Пулю посчитаны, львиная доля расчетов позади. Количество вистов каждого игрока за гору обычно записывается под именем игрока и обводится в круг или овал. Должно получится следующее:
4) Далее переходим к расчету взаимных вистов. Для этого смотрим картинку в статье и делаем взаимный расчет в соответствии с нарисованными стрелками. Стрелки указывают взаимные висты игроков друг на друга. После всех подсчетов должно получиться следующее.
5) Последний заключительных этап в расчетах – это сложение всех положительных очков и вычитание из суммы всех отрицательных очков каждого игрока. Получаем Итоговый результат игры. Результат записывается в поле ПУЛЯ заключенным в «модульные» скобки.
6) Проверка. Снова проверяем чтобы сумма положительных очков была равна сумме отрицательных очков. Если суммы не сходятся, то где-то неверно посчитали. Вернитесь и проверьте. СУММЫ ДОЛЖНЫ ОБЯЗАТЕЛЬНО СОЙТИСЬ!!! Если обратите внимание у нас в расчетах все правильно.
После того как рассчитан итоговый результат можно произвести окончательный расчет по игре. Мы посчитали количество вистов, которые проиграл или выиграл каждый игрок. Надеюсь, что перед игрой Вы договорились, сколько стоит Один Вист? Вот теперь эта договоренность вступает в силу. Умножаем рассчитанное количество вистов, на оговоренную величину ставки. Рассчитываемся.
Мы посчитали количество вистов, которые проиграл или выиграл каждый игрок. Надеюсь, что перед игрой Вы договорились, сколько стоит Один Вист? Вот теперь эта договоренность вступает в силу. Умножаем рассчитанное количество вистов, на оговоренную величину ставки. Рассчитываемся.
Теперь отличия расчетов для различных вариантов игры.
1) При игре на 3 человека, расчеты идентичны, за исключением того, что считаем на 3. То есть суммарную величину горы делим на 3. И при подсчете суммарной величины пули, которую надо закрыть, также используем число 3. Например, если договорились на величину пули до 21, то в 3 надо закрыть 63, а в 4 -84.
Привет, друзья!
Сегодня, как и обещал, рассмотрим расчет пули в преферансе , в процессе игры. Вот Вы сыграли игру Вам и вашим соперникам зачислили определенное количество очков. Сразу договоримся о какой системе игры идет речь. Рассматриваем вариант игры Сочинка. Распасы в игре не прогрессирующие, то есть 1, 2, 2, 2, … и т. д. Вист Джентельменский. Длина пули не важна. Итак начнем.
д. Вист Джентельменский. Длина пули не важна. Итак начнем.
Подсчет очков в игре ведется кратно тому количеству очков, величину игры которой Вы играете. Например, играет шестерную игру, все очки насчитываются кратными 2. Играем семерную игру – 4, восьмерную – 6, девятерную – 8, десятерную – 10. Рассмотрим подсчет очков для шестерной игры.
Количество очков в пулю . За шестерную игру начисляется 2 очка в пулю. Эти очки будут засчитаны игроку, игравшему игру при условии, что он взял 6 или более взяток. Если взяток было заказано шесть, а взято меньше, то игрок получит очки в гору.
Висты . Каждому вистующему будет начисляться по 2 очка за каждую взятую взятку на игрока, играющего игру. Предположим, что игрок1 сыграл 6 пик, при этом игрок2 взял 2 взятки. Игроку2 на игрока 1 положено 4 виста, что и фиксируется в соответствующей графе бланка для записи.
Количество очков в гору. За каждую недовзятую взятку при шестерной игре игроку полагается 2 очка в гору.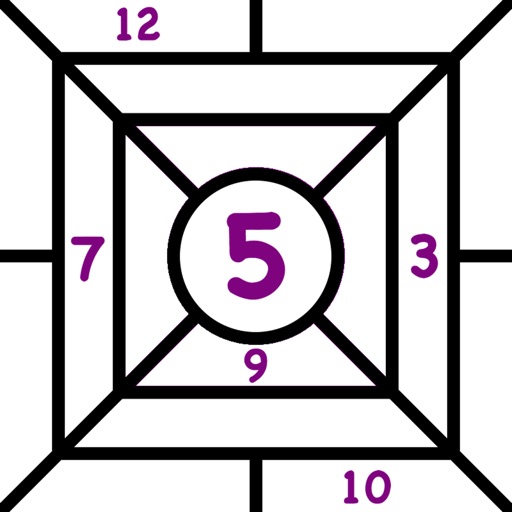 Причем это правило распространяется как на играющего игру, так и на вистующих игроков. Например, если игрок заказывал 6 пик, а взял при этом 7 взяток, то значит, кто-то из вистующих недобрал 1 взятку. Смотрим, у кого нет на руках двух взяток, тот и получает очки в гору. Второй при этом получает только висты.
Причем это правило распространяется как на играющего игру, так и на вистующих игроков. Например, если игрок заказывал 6 пик, а взял при этом 7 взяток, то значит, кто-то из вистующих недобрал 1 взятку. Смотрим, у кого нет на руках двух взяток, тот и получает очки в гору. Второй при этом получает только висты.
Распасы. При распасах все достаточно просто. Считаем количество взятых взяток у каждого игрока, умножаем их на величину очков за взятку (одинарные или двойные распасы) и записывает данную величину в гору игрока. Например, в игре идет третий круг распасов (то есть уже двойные), игрок1 берет 3 взятки, игрок2 берет 2 взятки, игрок3 берет 5 взяток, соответственно игрок1 получит 6 очков в гору, игрок2 – 4, игрок3 – 10.
Для упрощения оконечных расчетов и поскольку это никак не повлияет на конечный результат рекомендуется следующая схема подсчета очков в гору при распасах. 1)Находим игрока у которого минимальное количество взяток (в нашем примере это игрок2 в 2 взятками) 2) Вычитаем минимальное количество взяток у оставшихся игроков 3) На оставшееся количество взяток у игроков начисляем очки в гору.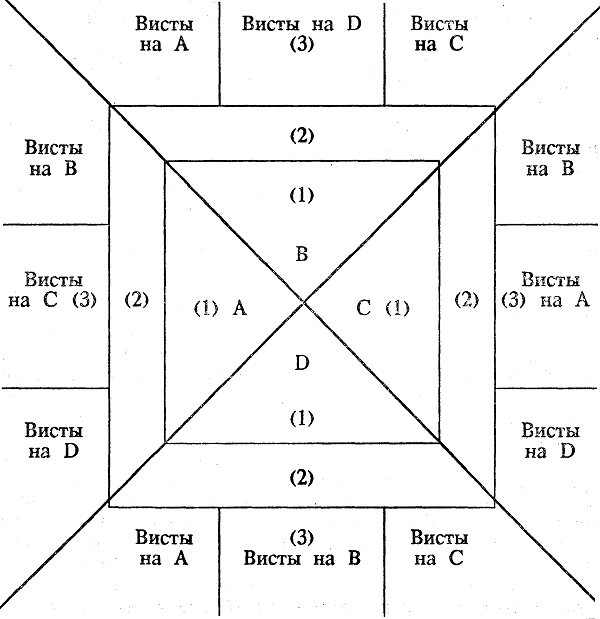
В нашем примере получим следующее: 1) У игрока2 всего 2 взятки 2) После вычитания у остальных игроков 2 взяток останется: Игрок1 – 1 взятка, Игрок 3 – 3 взятки. 3) По итогам записываем игроку1 – 2 в гору, игроку2 – 0 в гору, игроку3 – 6 в гору.
Если обратите внимание, то мы просто вычли у всех игроков по 4 очка в гору и все! Это нам существенно упростит расчет конечного результата.
Теперь отдельный случай, когда игрок «обламывается» и не играет заказанную игру, или, как говорят на карточном жаргоне, «остается без лап». В этом случае игроку за каждую недобранную взятку начисляют очки в гору. Пусть при шестерной игре он взял только 5 взяток, остался «без одной лапы». В этом случае ему засчитывается 2 очка в гору, никаких очков в пулю. Также вистующим товарищам, которые совершили это действо, начисляются дополнительные бонусы в виде дополнительных вистов. А именно, к числу набранных взяток вистующего добавляется еще одна взятка (которую недобрал играющий) и умножается на очки игры (в нашем примере на 2).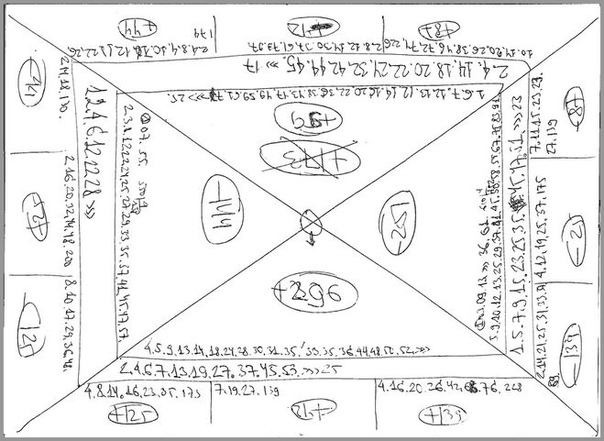 Таким образом рассчитывается конечное количество вистов. Если, к примеру, один вистующий взял 5 взяток, а второй при этом пасовал или вистовал но взял 0 взяток, то висты рассчитываются следующим образом: первому достается (5+1)*2 = 12 вистов, а второму достается 2 виста «за облом». Соответственно, если игрок недобрал 2 взятку, то плюсуем эти две взятки каждому из вистующих.
Таким образом рассчитывается конечное количество вистов. Если, к примеру, один вистующий взял 5 взяток, а второй при этом пасовал или вистовал но взял 0 взяток, то висты рассчитываются следующим образом: первому достается (5+1)*2 = 12 вистов, а второму достается 2 виста «за облом». Соответственно, если игрок недобрал 2 взятку, то плюсуем эти две взятки каждому из вистующих.
Преферанс онлайн на деньги
Правила онлайн игр
Преферанс
Преферанс на деньги
Небольшой экскурс в правила игры преферанс
Игра преферанс на деньги предусматривает колоду в 32 карты, от семерки (младшая карта) до туза (старшая) каждой масти. Также, стоит отметить, для записи очков в игре преферанс используется специально размеченный лист – так называемая пулька. Каждый из игроков имеет в пульке 3 области:
Пуля – происходит запись очков за сыгранные партии на взятки и премия за 0 взяток.
Скачать игру на компьютер
Играть с реальными людьми (бесплатно)
Каждое очков в пуле равняется +10 либо +20 вистам.
Гора – поле штрафных очков в игре преферанс . Записываются виста за ремизы и за взятки на распасах. Очков в гору равно -10.
Висты – начисляются очки за взятки при вистовании, за наименьшее количество взяток. Когда идет подсчет в игре преферанс, то учитывают и разность вистов каждого участника.
Каждая партия в игре преферанс состоит из совокупности раздач карт, где происходит один из трех возможных видов игры. Партия в преферансе продолжается до тех пор, пока не выполнится условия ее окончания, которые предварительно обговаривают участниками игры:
Каждый из игроков набрал установленное количество очков в пуле,
Игроки в преферанс, в общем, набрали определенное количество очков в пуле,
Наступило время окончания игры, по договоренности,
Отыграно определенное количество раздач, оговоренное,
Набраны очки в пуле и гора игроков обнуляется.
Раздача карт в игре преферанс
Играть в преферанс на деньги желательно четверым участникам, так как при большем количестве динамика игры теряется.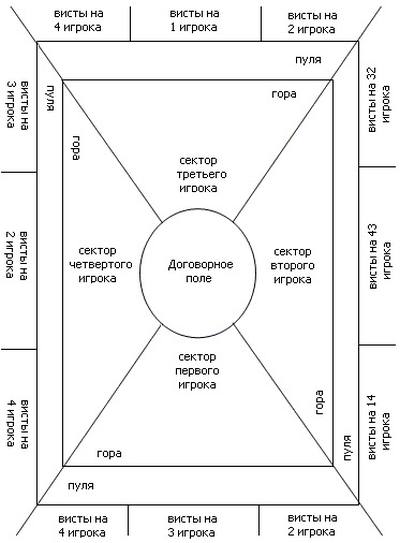 Игрок на раздаче должен тщательно перетасовать карты, после чего положить колоду соседу справа, для срезания. Положив оставшуюся колоду в игре преферанс, он раздает их.
Игрок на раздаче должен тщательно перетасовать карты, после чего положить колоду соседу справа, для срезания. Положив оставшуюся колоду в игре преферанс, он раздает их.
Карты необходимо раздавать по две за один раз, по часовой стрелке, начиная с левого участника. В итоге у каждого игрока по 10 карт. При игре в преферанс откладывается 2 карты отдельно в «прикуп».
При игре преферанс на деньги, игрок, победивший в торге, берет карты прикупа и оставляет их себе, предварительно показав их всем участникам.
Существует онлайн преферанс на деньги. На нашем сайте. возможно, посоревноваться с другими игроками по Интернету, для этого необходимо выбрать стол, после чего начнется игра, если стол набрал нужное количество игроков. Помните, что победа зависит только от умения игрока.
Для начала игры в нарды онлайн нужно пройти регистрацию и выбрать себе соперника.
Интересное видео по теме
Cообщество любителей преферанса Молдовы
В сооздавшейся из-за [censored] коронавируса обстановке традиционный новогодний турнир среди кишиневских преферансистов Mos Craciun провести в обычном порядке не представляется возможным.
Но, поскольку живем мы не в каменном веке, а в пору широкого распространения интернета – турнир проведен будет. Онлайн, на одном из игровых серверов.
Схема – прежняя: 16 игроков за 5 туров сыграют в пулях на четверых каждый с каждым ровно один раз. Длина каждой пули – 100 минут, перерывы между – 20 мин.
Причем, если на очный турнир участникам приходилось выделять весь день, что затруднительно как в плане занятости, так и в плане усталости, то в этом случае появляется техническая возможность сыграть в одно из воскресений, например, три тура, а в следующее – оставшиеся два. Или наоборот.
Предварительный план: играть два воскресенья, 13 и 20 декабря, начав с 10 утра.
Для участия в турнире следует подать заявку на электрическую почту info@pref.md с того адреса, который будет зарегистрирован на игровом сервере (см. ниже). В ответном письме заявителю будет выслана ссылка для регистрации на сервере. Да, вот так конспиративно Там все просто делается, разобраться несложно, проверено. И потом, преферансисты ведь по умолчанию умные, они умеют считать по крайней мере до восьми… Примечание: функция самостоятельного пополнения счета на сервере имеется, но пользоваться ею пока не надо.
И потом, преферансисты ведь по умолчанию умные, они умеют считать по крайней мере до восьми… Примечание: функция самостоятельного пополнения счета на сервере имеется, но пользоваться ею пока не надо.Далее участник (а вот это все-таки живьем придется делать) сдает Сан Санычу взнос, состоящий из двух частей:
— взнос в призовой фонд турнира в обычном размере 1000 MDL. Выдача призовых (как обычно, за 1 – 4 места в турнире) будет произведено упомянутым АА в очном же порядке (только не толпитесь перед дверью его кабинета!)
— и взнос организационный, по EUR 10 с каждого. Эти 10 евро будут административным путем (так надо…) внесены на счет каждого игрока на игровом сервере и использованы (в малой части) для оплаты собственно участия в турнире, а также компенсации административных и орграсходов. Кстати, эта часть взноса получится меньше, чем аналогичная для очника.
Все неизрасходованное (а это, скорее всего, будет существенная часть от десятки) – остаётся на счету игрока, и он сможет использовать эти средства для игры на сервере уже сам по себе, безотносительно завершившегося турнира. И потом играть в любое удобное для него время. Находясь онлайн, этот [censored] ковид – не страшен
И потом играть в любое удобное для него время. Находясь онлайн, этот [censored] ковид – не страшенСпешите заявиться, количество мест ограничено. Нерезидентов РМ просьба не беспокоиться.
В создавшейся из-за [censored] коронавируса обстановке традиционный новогодний турнир среди кишиневских преферансистов Mos Craciun провести в обычном порядке не представляется возможным.
Но, поскольку живем мы не в каменном веке, а в пору широкого распространения интернета — турнир проведен будет. Онлайн, на одном из игровых серверов.
Схема – прежняя: 16 игроков за 5 туров сыграют в пулях на четверых каждый с каждым ровно один раз. Длина каждой пули – 80 минут, перерывы между – 10 мин.
Причем, если на очный турнир участникам приходилось выделять весь день, что затруднительно как в плане занятости, так и в плане усталости, то в этом случае появляется техническая возможность сыграть в одно из воскресений, например, три тура, а в следующее – оставшиеся два. Или наоборот.
Или наоборот.
Предварительный план: играть два воскресенья, 13 и 20 декабря, начав с 10 утра. Хотя это – обсуждаемо.
Для участия в турнире следует подать заявку на электрическую почту info@pref.md с того адреса, который будет зарегистрирован на игровом сервере (см. ниже). В ответном письме заявителю будет выслана ссылка для регистрации на сервере. Да, вот так конспиративно Там все просто делается, разобраться несложно, проверено. И потом, преферансисты ведь по умолчанию умные, они умеют считать по крайней мере до восьми… Примечание: функция самостоятельного пополнения счета на сервере имеется, но пользоваться ею пока не надо.
Далее участник (а вот это все-таки живьем придется делать) сдает Сан Санычу взнос, состоящий из двух частей:
— взнос в призовой фонд турнира в обычном размере 1000 MDL. Выдача призовых (как обычно, за 1 – 4 места в турнире) будет произведено упомянутым АА в очном же порядке (только не толпитесь перед дверью его кабинета!)
— и взнос организационный, по USD 10 с каждого. Эти 10 баксов будут административным путем (так надо…) внесены на счет каждого игрока на игровом сервере и использованы (в малой части) для оплаты собственно участия в турнире, а также компенсации административных и орграсходов. Кстати, эта часть взноса получится в два раза меньше, чем аналогичная для очника.
Эти 10 баксов будут административным путем (так надо…) внесены на счет каждого игрока на игровом сервере и использованы (в малой части) для оплаты собственно участия в турнире, а также компенсации административных и орграсходов. Кстати, эта часть взноса получится в два раза меньше, чем аналогичная для очника.
Все неизрасходованное (а это, скорее всего, будет существенная часть от десятки) – остаётся на счету игрока, и он сможет использовать эти средства для игры на сервере уже сам по себе, безотносительно завершившегося турнира. И потом играть в любое удобное для него время.
Находясь онлайн, этот [censored] covid – не страшен
Спешите заявиться, количество мест ограничено. Нерезидентов РМ просьба не беспокоиться.
Скоропостижно скончался Виктор Безверхний (”Трудный”).
Ему было 63 года. На протяжении десятилетий Виктор Петрович вносил неоценимый вклад в развитие преферанса в Молдове.
Он являлся практически бессменным судьей проводимых в Кишиневе преферансных турниров, начиная с самого первого “Мош Крэчун”, состоявшегося давным-давно практически под дулами полицейских автоматов. Также Петрович уверенно и беспристрастно работал судьей на всех ОПМД, был при этом строг и принципиален, невзирая на лица, авторитеты и знакомства, на практике подтверждая свой игровой ник.
Также Петрович уверенно и беспристрастно работал судьей на всех ОПМД, был при этом строг и принципиален, невзирая на лица, авторитеты и знакомства, на практике подтверждая свой игровой ник.
Существенную роль Трудный сыграл и в онлайн-преферансе. И как один из первых судей Gambler, и как член молдавской команды “Аист пик”.
Участник многочисленных очных встреч, в том числе международных (как в Кишиневе, так и на зарубежных выездах) – Витя своим тонким, острым юмором и неизменным обаянием делал эти мероприятия незабываемыми. А еще с ним было удобно играть при слабом освещении.
Преферансисты Молдовы выражают глубокие соболезнования друзьям, близким и родным покойного.
Следующий (планируемый в декабре) турнир “Мош Крэчун” будет посвящен памяти Виктора Безверхнего.
Скоропостижно скончался Виктор Безверхний (”Трудный”).
Ему было 63 года. На протяжении десятилетий Виктор Петрович вносил неоценимый вклад в развитие преферанса в Молдове.
Он являлся практически бессменным судьей проводимых в Кишиневе преферансных турниров, начиная с самого первого “Мош Крэчун”, состоявшегося давным-давно практически под дулами полицейских автоматов. Также Петрович уверенно и беспристрастно работал судьей на всех ОПМД, был при этом строг и принципиален, невзирая на лица, авторитеты и знакомства, на практике подтверждая свой игровой ник.
Существенную роль Трудный сыграл и в онлайн-преферансе. И как один из первых судей Gambler, и как член молдавской команды “Аист пик”.
Участник многочисленных очных встреч, в том числе международных (и в Кишиневе, и на зарубежных выездах) – Виктор своим тонким, острым юмором и неизменным обаянием делал эти мероприятия незабываемыми. А еще с ним было удобно играть при слабом освещении.
Преферансисты Молдовы выражают глубокие соболезнования друзьям, близким и родным покойного.
Следующий (планируемый в декабре) турнир “Мош Крэчун” будет посвящен памяти Виктора Безверхнего.
После тяжелой болезни скончался неоднократный победитель и призер кишиневских турниров по преферансу Олег Соколов.
Клубы интеллектуальных игр “Dama blank”, “Lavintal” и “Singleton” выражают глубокие соболезнования родным и близким покойного.
Неоднократный победитель и призер чемпионатов Беларуси и других преферансных турниров Армен Маркарян умер 19 декабря в Минске на 62-м году жизни после тяжелой продолжительной болезни.
Молдавское префсообщество выражает глубокие соболезнования родным, друзьям и близким Армена и скорбит вместе с ними.
Традиционный новогодний турнир “для внутреннего пользования” Mos Craciun прошел в этом году суть раньше обычного. Но не хуже обычного.
По итогам длившихся весь световой день пяти туров по принципу “каждый с каждым играет ровно один раз” призерами стали:
1) Виталий Апостол
2) Сергей Молчанов
3) Павел Гроссу
4) Геннадий Топоревский
Полная таблица результатов здесь
Mos Craciun 2019 participants
Турнир Отдых 2019
Отель Аквапарк Zusterna ***
Koper Slovtnia
3–11августа
Стоимость отеля с 2х разовым питанием
2х местный номер 102 Евро
1 66. 50
50
3 145.50
Дети до 5.99 лет 00.00
от 6 до 11.99 25.50
Дополнительные расходы
Тах 2 евро в сутки+регистрация 1.50 (1 раз)
Турнир 9 туров 150/100
0.15 Евро/ вист
2—3 экскурсии по Словении и Истрии( Хорватия)
возможен шопинг тур в Милан.
Ближайшие Аэропорта: Триест Италия
Пула Хорватия
Любляна Словения
Прошу срочно присылать Ваши заявки
Оргкоммитет
Изя Асинас iasinass@mail.ru
49 15787504228
49 26129638281
Корец Владимир 49 17661252525
Турнир – отдых 2019
Отель Аквапарк Zusterna ***
Koper Slovenia
3 по 11 августа
Стоимость отеля с двухразовым питанием
2х местный номер 102 Евро
1 66.50
3 145.50
Дети до 5,99 лет 00. 00
00
от 6 до 11,99 25.50
Дополнительные расходы
Тах 2 евро в сутки+регистрация 1.50 (1 раз)
Турнир по традиционной формуле
9 туров 150/100
0.15 Евро/ вист
Возможна организация 2-3 экскурсий по Словении и Истрии (Хорватия)
Также возможен шопинг-тур в Милан.
Ближайшие аэропорты:
Триест (Италия)
Пула (Хорватия)
Любляна (Словения)
Желающих принять участие просьба срочно присылать заявки
Оргкомитет
Изя Асинас iasinass@mail.ru
+49 15787504228
+49 26129638281
Корец Владимир +49 17661252525
Дорогие Друзья13 апреля 2019 года Сергей Истратов отмечает свой 60-ти летний юбилей. От имени и по просьбе юбиляра, Международная лига интеллектуальных игр Германии, приглашает вас в один из великолепных городов Европы с мировым именем – Прагу , на турнир по преферансу.
Турнир состоится с 11 – 15 апреля 2019 года.
Предлагаем вам проживание в отеле «DUO“. ****
****
Преимущества: метро в трех минутах ходьбы от отеля и 10-ти минутах езды до центра
В стоимость входит: отличнейший завтрак, бассейн, сауна , тренажерный зал.
У отеля есть своя парковка и самое главное: живое КАЗИНО!!
Стоимость одного двухместного номера в сутки с завтраком -70€
Одноместный номер – также 70€
План мероприятия:
Турнир: 9 туров, 150/150 € ставка 0.15 евро/ центов
11/ 04 – день заезда 12 ,13, 14/ 04 – игровые дни , 13/04 вечером – банкет
Участники турнира обеспечиваются обедом
15 /04 – для желающих автобусно-пешеходная экскурсия по нижней и верхней Праге.
Оргкомитет: Асинас Надежда, Изак + 4926129638281домашний
( есть автоответчик) iasinass@mail.ru
Wats Ap ,Viber +491734836134 Надеждa , +49 15787504228 Изак
+4917661252525 Володя Корец
Убедительная просьба :сделать предварительную заявку
Оказываем визовую поддержку!
Дорогие друзья!
13 апреля 2019 года Сергей Истратов отмечает свой 60-ти летний юбилей.
От имени и по просьбе юбиляра, Международная лига интеллектуальных игр Германии приглашает вас в один из великолепных городов Европы с мировым именем – Прагу на турнир по преферансу.
Турнир состоится с 11 – 15 апреля 2019 года.
Предлагаем вам проживание в отеле «DUO“.****
Преимущества: отель находится в трех минутах ходьбы от метро и 10-ти минутах езды до центра.
В стоимость входит: отличнейший завтрак, бассейн, сауна, тренажерный зал.
У отеля есть своя парковка и, самое главное: живое КАЗИНО!!
Стоимость одного двухместного номера в сутки с завтраком = €70
Одноместный номер – также €70
План мероприятия:
Турнир: 9 туров, 150/150 €, ставка 0.15 евроцентов
11 апреля – день заезда
12 ,13, 14 апреля – игровые дни,
13 апреля вечером – банкет.
Участники турнира обеспечиваются обедом.
15/04 – для желающих автобусно-пешеходная экскурсия по нижней и верхней Праге.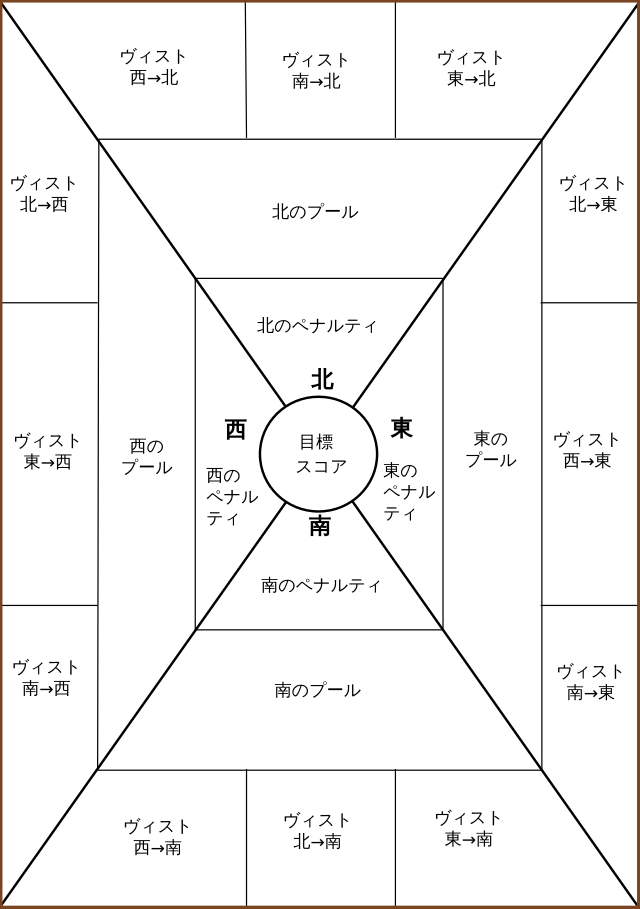
Оргкомитет: Асинас Надежда, Изак + 49 26129638281 домашний (есть автоответчик)
iasinass@mail.ru
WhatsApp, Viber +49 1734836134 Надеждa,
+49 15787504228 Изак,
+49 17661252525 Володя Корец
Убедительная просьба: сделать предварительную заявку
Оказываем визовую поддержку!
Решением Международной Лиги Преферанса за период с 01.01.2013 по 31.12.2017 звания Международного Мастера Преферанса удостоены 15 игроков, один из которых:
Юрий Северин (Кишинёв)
В числе тех 21 игроков, кто подтвердил уровень мастерства, показанный за этот же период – кишиневец Константин Шпак
По результатам периода с 01.01.2013 по 31.12.2017 звания действующего Международного Мастера Преферанса удостоены ещё 27 игроков, среди которых и представитель Молдовы Николай Голик
Всего в МЛП по состоянию на апрель 2018:
7 действующих Международных Гроссмейстеров Преферанса,
22 действующих Гроссмейстера Преферанса,
и 63 действующих Международных Мастера Преферанса
На прошедшем в конце марта в Минске (Беларусь) очередном Чемпионате мира разыгрывались титулы в двух категориях.
Профессионал:
Чемпионом мира стал Вадим Терехов, международный гроссмейтер из города Пермь (Россия)
второе место занял Юлий Шлепер, мастер преферанса, Москва (Россия)
третьим оказался Владимир Аболишин, гроссмейстер преферанса, Челябинск (Россия)
Полная таблица мест здесь
Мастер:
Чемпион мира – Игорь Фомичёв, мастер преферанса, Смоленск (Россия)
вторым был Виктор Медушевский, гроссмейстер преферанса, Киев (Украина)
третьим – Александр Фридман, гроссмейстер преферанса, Самара (Россия)
все участники перечислены в этой таблице
Молдавских атлетов на турнире, к сожалению, не наблюдалось.
В ходе проведенного недавно турнира Mos Craciun 2017 (см. предыдущую запись) внезапно образовался еще один (сверх запланированных) приз.
Один из членов Кишиневского преф-клуба – Вадим Степанович Демянчук – организуя для сотрудников своей фирмы поездку на горнолыжный курорт Буковель, любезно предоставил одно место в автобусе и гостинице для коллег-преферансистов.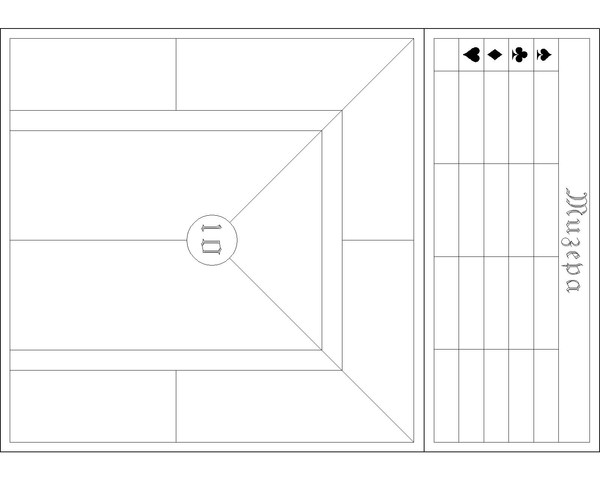
Поскольку эта инициатива оказалась совсем неожиданной, а более подробных условий для получателя приза озвучено не было – идея разыграть его вытаскиванием карты из колоды вполне всех устроила. После иключения из списка претендентов тех четырех, что уже поделили между собой призовой фонд собственно преф-турнира, осталось 12. И удачливую карту из колоды вынимали “нейтральные” люди.
В общем, поехал туда Владимир Супрун. А чем там занимался – видно из фото.
Клубы любителей преферанса Dama Blank, Lavintal и Singleton, а также лично В. Супрун благодарят Вадима Степановича Демянчука за идею и ее реализацию.
Какая масть самая старшая в преферансе. Преферанс-общие правила
Преферанс-общие правила
Карточная игра преферанс. бесспорно, игра умная и увлекательная, интересен большим разнообразием приемов и не слишком утомителен. Времени для его изучения требуется меньше, чем для винта. Но все-таки, чтобы уметь хорошо играть в преферанс, нужен навык и большой опыт.
Но это придет со временем. Для начала же необходимо выучить правила игры преферанс и отлично в них разбираться.
Правила преферанса допускают игру с разным колличеством игроков вдвоем, втроем, вчетвером и впятером.
Самая лучшая и самая верная игра вчетвером. В этой игре шансы для всех игроков равны и самый слабый игрок рискует очень немногим.
1) Для преферанса используется колода в 32 карты, такая же, колода карт (короткая) как и в пикет. Порядок карт следующий: туз, король, дама, валет, десятка, девятка, восьмерка, семерка. Что по правилам игры преферанс. в отношении других карточных игр совсем не является необычным
2) Порядок мастей таков: пики, трефы, бубны и червы.
3) Вся колода карт сдается на троих, причем четвертая пара карт откладывается для прикупа.
4) В правилах преферанса четко оговаривается, что сдавать следует обязательно по две карты.
5) Сдача производится в обычном порядке, по очереди. Места выбираются по картам.
6) Козырей на вскрышке не полагается, каждый играет в той масти, которая, по его мнению, выгодна и возможна для правильного разыгрывания.
7) По сдаче карт первым назначает игру сидящий слева от сдатчика, объявляя пики, второй может прикупать к трефам, третий к бубнам или, если у него масть именно трефовая, на которой он предполагал играть, может сказать: «Держу» (т. е. «И я прикупаю к трефам»), После него наступает очередь говорить первому игроку, который объявляет бубны; если третий держал, трефы, или говорит: «Держу бубны», если третий держал трефы или говорит: «Держу бубны», если третий сказал: «Бубны». Следующий за ним объявляет червы, затем опять слово за третьим.
Если у последнего нет игры выше черв, т. е. бескозырной или на семь, то он говорит: «Пас», в противном же случае поднимает выше, т. е. назначает без козырей. За ним первый игрок объявляет семь пик и т. д. игра поднимается в том же порядке до тех пор, пока два игрока не спасуют и не отдадут прикуп третьему. Торговля может идти до десяти без козырей, причем повышать игру следует в строгом порядке мастей.
8) Раз спасовавший не имеет больше права на торговлю прикупом в эту игру.
9) Игрок, купивший на семь, не имеет права играть простых, а купившему на восемь нельзя играть семь. Вообще-то по правилам игры преферанс играть меньше, чем прикупил, не разрешается.
Если игроку покупку уступили на семь бубен, то он не может играть семь пик или треф, а должен в этих мастях играть уже восемь. В бубнах же, червах и без козырей имеет право играть семь. Так же поступают при всех покупках, старшинство мастей соблюдается строго.
10) Взявший прикуп должен показать его играющим. Две карты, сбрасываемые им вместо покупки, он никому не показывает, и смотреть их никто не имеет права.
11) На руках каждого игрока должно быть по десять карт.
12) До окончания сдачи ни один, игрок не должен трогать своих карт, а тем более смотреть их, чтобы не было каких-либо претензий игроков в случае за сдачи.
13) Колоду карт снимает сосед с правой стороны. Первый выход всегда принадлежит тому, кто сидит слева от сдатчика, последующие выходы получившему взятку.
14) Карты пересдаются: если во время сдачи какая-нибудь карта нечаянно вскроется; если у одного из играющих окажется на руках карт больше, а у другого меньше; если сдача произведена не в очередь и эта ошибка вовремя замечена, т. е. никто еще своих карт не смотрел.
15) В игре вчетвером сдатчик не должен смотреть прикуп во избежание, каких бы то ни было недоразумений, а так же не должен смотреть в карты соседа и тем более ему советовать, даже если он его об этом попросил. Но такого правила в преферансе мало кто придерживается, потому что скучно просидеть целую игру в бездействии, но нарушителям его могут быть сделаны справедливые замечания.
16) Никто раньше самого прикупившего не имеет права смотреть прикуп, в противном случае виновник ставит ремиз в объявленной прикупившим масти и лишается права вистовать в эту игру.
17) В переговорах очередь соблюдается строго, чтобы никого не вводить в обман и не запутывать игру как свою, так и партнеров.
18) При переговорах каждый игрок обязан договаривать свои масти до конца, если уж он начал торговаться, а не останавливаться на полдороге, потому что такое неправильное объявление своей масти вводит в заблуждение партнера, которого он в случае обоюдного виста совершенно невольно может подвести под ремиз.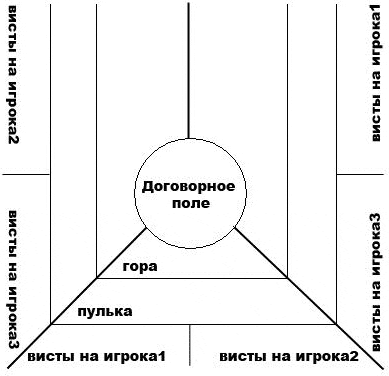
— общие правила преферанса и его разновидности
Карточная игра преферанс, бесспорно, игра умная и увлекательная, интересен большим разнообразием приемов и не слишком утомителен. Чтобы уметь хорошо играть в преферанс, нужен навык и опыт. Но это придет со временем.
Для начала же необходимо выучить правила игры преферанс и отлично в них разбираться.
Правила популярной карточной игры Тысяча
Тысяча (1000) уже давно принадлежит к разряду, самые популярные карточные игры, и с этим не поспорить. Не имеет смысла разбираться в причинах такой популярности, а следует просто принять этот факт. Самый интересный и популярный вариант правил карточной игры 1000 (тысяча), это игра для трех участников.
Азартная игра? Нет сомнений.
Какое название мы бы не использовали всем сразу понятно, о чем пойдет речь.
Эта игра принадлежит к разряду азартных игр вроде — баккара, макао и др. Вся разница между теми играми и Блэк Джек в счете очков и значении фигур.
Для преферанса употребляется колода в 32 карты. Порядок карт от старшей масти к младшей следующий: Туз, Король, Дама, Валет, Десятка, Девятка, Восьмерка и Семерка.
Порядок карт от старшей масти к младшей следующий: Туз, Король, Дама, Валет, Десятка, Девятка, Восьмерка и Семерка.
Порядок мастей от младшей к старшей таков: пики , трефы , бубны .
Вся колода сдается на троих, причем одна пара карт (не первая и не последняя) откладывается для прикупа.
Сдавать следует обязательно по две карты.
Сдача производится в обычном порядке, по очереди. Места выбираются по картам.
Козырей на вскрышке не полагается, каждый игрок играет в той масти, которая по его соображению выгодна и возможна для правильного разыгрывания.
По сдаче карт, первым объявляет игру сидящий слева от сдатчика. Говоря «пики», он тем самым заявляет, что готов взять прикуп и, назначив козырем пики, взять шесть взяток. Пики — самая младшая масть, а шесть взяток — тот минимум, который возможен при игре. Второй может прикупать к трефам, третий к бубнам, или, если у него масть именно трефовая, на которой он предполагал играть, может сказать «держу» или «здесь», (т. е. и я прикупаю к трефам). После него очередь говорить подходит к первому игроку, который говорит бубны, если третий держал трефы, или говорит держу бубны, если третий сказал бубны. Следующий за ним говорит черви, за ним опять слово за третьим. Если у послзднего нет игры выше червей, т. е. бескозырной или на семь, то он говорит «пас», в противном же случае поднимает выше, т. е. говорит без козырей. За ним говорит первый игрок «семь пик» (т. е. уже он берет семь взяток на пиках) и игра поднимается в том же порядке до тех пор, пока два игрока не спасуют и не отдадут прикупку третьему. Торговля может идти до 10 без козырей, причем возвышать игру следует в строгом порядке мастей и взяток.
е. и я прикупаю к трефам). После него очередь говорить подходит к первому игроку, который говорит бубны, если третий держал трефы, или говорит держу бубны, если третий сказал бубны. Следующий за ним говорит черви, за ним опять слово за третьим. Если у послзднего нет игры выше червей, т. е. бескозырной или на семь, то он говорит «пас», в противном же случае поднимает выше, т. е. говорит без козырей. За ним говорит первый игрок «семь пик» (т. е. уже он берет семь взяток на пиках) и игра поднимается в том же порядке до тех пор, пока два игрока не спасуют и не отдадут прикупку третьему. Торговля может идти до 10 без козырей, причем возвышать игру следует в строгом порядке мастей и взяток.
Раз спасовавший не имеет более права на торговлю прикупки в эту игру.
Игрок, купивший на семь, не имеет права играть простых, так же купивши на восемь, нельзя играть семь. Вообще играть менее, нежели прикупил, не позволяется. Если игроку покупку уступили на семь бубен, то он не может играть семь пик или треф, а должен в этих мастях играть уже восемь. В бубнах же, червях и без козыря имеет право играть семь. Так же поступают при всех покупках; старшинство мастей соблюдается строго.
В бубнах же, червях и без козыря имеет право играть семь. Так же поступают при всех покупках; старшинство мастей соблюдается строго.
Взявший прикуп, должен показать его играющим. Две же карты, сбрасываемые им вместо покупки, он никому не показывает и смотреть их никто не имеет права.
На руках каждого игрока должно быть по десять карт.
До окончания сдачи ни один игрок не должен трогать своих карт, а тем более смотреть их, чтобы не было каких-либо претензий игроков в случае засдачи.
Колоду снимает сосед с правой стороны. Первый выход всегда принадлежит тому, кто сидит налево от сдатчика; последующие — кто возьмет взятку.
Карты пересдаются: если во время сдачи какая-нибудь карта нечаянно вскроется; если у одного из играющих окажется на руках карт больше, а у другого меньше; если сдача произведена не в очередь, и вовремя эта ошибка замечена, т. е. никто еще своих карт не смотрел.
В игре вчетвером сдатчик не должен смотреть прикупку, во избежание каких бы то ни было недоразумений, а равно не должен смотреть в карты соседа, а тем более ему советовать, хотя бы по его же просьбе. Этого правила редко придерживаются, потому что скучно просидеть целую игру в бездействии, но за это нередко заслуживают вполне основательные нарекания. Однако любой игрок имеет право позвать сдающего играть «в пополаме» (по некоторым правилам — только 10 или мизер — чтобы не было проблем с вистами). В этом случае вся ответственность делится пополам (отсюда название), ровно как и выигрыш. Если прикупающий не утерпел и посмотрел прикуп, его уже нельзя звать «в пополам» (а следует дать по шее).
Этого правила редко придерживаются, потому что скучно просидеть целую игру в бездействии, но за это нередко заслуживают вполне основательные нарекания. Однако любой игрок имеет право позвать сдающего играть «в пополаме» (по некоторым правилам — только 10 или мизер — чтобы не было проблем с вистами). В этом случае вся ответственность делится пополам (отсюда название), ровно как и выигрыш. Если прикупающий не утерпел и посмотрел прикуп, его уже нельзя звать «в пополам» (а следует дать по шее).
Никто, ранее самого прикупившего, не имеет права смотреть прикуп, в противном случае виновник ставит ремиз в объявленной прикупившим масть, и лишается права вистовать в эту игру.
В переговорах (торговле) очередь соблюдается строго, дабы никого не вводить в обман и не запутывать игры, как своей, так равно и партнеров.
При переговорах важно договаривать свои масти до конца, если уж начал торговаться, а не останавливаться на полдороги, потому что такое неправильное объявление своей масти введет в заблуждение партнера, и, при случае обоюдного виста, он совершенно невольно может вас подвести под ремиз.
Не имея верных взяток, а в особенности не имея верного выхода, не следует вистовать. Верный выход для внимательного игрока, впрочем, суть нетрудная, так как он всегда знает (если, разумеется, переговоры ведутся правильно), каких мастей у назначившего игру нет. Выход следует делать с масти, до которой торговался другой вистующий или с своей собственной, но эта своя собственная должна иметь туза-короля сам-третей или четверть, или же туза не менее как сам- пять. Ход должен быть в первом случае с туза, короля и маленькой подряд, во втором — с туза и маленькой.
Вистующему следует ходить: под играющего с маленькой, (т. е. когда играющий сидит слева), и под вистующего (т.е. когда играющий сидит справа или напротив) с самой большой карты.
Торговаться советуем имея уже на руках пять взяток, в расчете на прикупную. При шести имеющихся взятках — покупать на семь, при семи — на восемь. При восьми имеющихся на руках поку пать на девять не советуем, потому что на прикупную взятку рассчитывать совершенно невозможно в тех видах, что партнер, так продолжительно торгующийся, должно быть имеет сильные карты. По теории вероятности — в прикупе фески чужой масти.
По теории вероятности — в прикупе фески чужой масти.
Когда объявится игра (т.е. один взял прикуп и сделал окончательную заявку), играющие могут вистовать или пасовать, смотря по своим картам. Желающий вистовать говорит:
— Вист!
А не желающий:
— Пас!
Большие переговоры допускаемы быть не должны. Класть карты следует по очереди, а не забегать вперед другого.
Если первый из возможных вистов говорит «пас», второй может отойти «за свои», но первый может сказать «фиг тебе, играем» и тем самым идет вист. Свои: на шести это две, на семи — одна взятка. На восьми и более «своих» не бывает.
Это очень удобное правило, позволяющее наказывать перестраховщиков, идущих 6 при 8-ми. В этом случае недозакладывающийся наказывает только себя. При Сталинграде «своих» нет. При игре «за свои» розыгрыш не производится (см. пункт 39).
Карта снесенная уже, переменена на другую быть не может, несмотря даже на то, что взятка еще не закрыта.
Разговоры во время разыгрывания, касающиеся игры, допускаемы быть не должны. Вистующие не имеют права подсказать друг другу о пропуске той или другой карты, или с какой карты ходить, или что сбрасывать и что держать.
Вистующие не имеют права подсказать друг другу о пропуске той или другой карты, или с какой карты ходить, или что сбрасывать и что держать.
На каждую требуемую масть нужно давать такую же масть.
Если же требуемой масти нет — должно перекрывать ее козырем.
Сносить же по произволу можно только тогда, когда нет ни этой масти, ни козырей.
Если кто, не имея масти, с которой ходят, и имея козырей, не побьет вышедшую карту козырем, или, имея на руках эту масть, сбросит на нее другую какую-либо или побьет ее козырем, признается сделавшим ренонс.
Если ренонс cделан играющим, то взятка эта переходит к тому вистующему, чья карта в требуемой масти старшая. Сделавший ренонс платит вистующим сколько следует по расчету за сделанные ими взятки, и если последние, вследствие этой ошибки, остались без одной или более, то ремиза не ставят, а ставит весь ремиз играющий.
Если же ренонс сделан вистующим, то играющий, хотя бы он и не сделал законное число взяток, списывает с игры столько, сколько ему следовало бы записать при выигрыше, и ремиза не ставит. Кроме этого, от сделавшего ренонс, отбираются без всяких рассуждений и проверок (раз факт ренонса установлен) взятки, неправильно им взятые, и провинившийся ставит за недобранные взятки и за каждый ренонс по одному ремизу по игре.
Кроме этого, от сделавшего ренонс, отбираются без всяких рассуждений и проверок (раз факт ренонса установлен) взятки, неправильно им взятые, и провинившийся ставит за недобранные взятки и за каждый ренонс по одному ремизу по игре.
Если бы играющий узаконенное число взяток и не делал и во всяком случае должен был бы остаться без одной или более, а вистующий сделал ренонс, то он, невзирая ни на какие доводы — ремиза не ставит и с игры списывает ту цифру, какую он списал бы при удачном розыгрыше. В игре с ренонсом никакие явные ремизы не признаются.
Когда же играющий и вистующий сделают ренонсы в одну и ту же игру, то за все отвечают они оба, а ренонсовые взятки принадлежат тому, чьи старшие карты; играющий и вистующий ставят по одному ремизу за каждый сделанный ими ренонс, и платят пополам по расчету другому вистующему за сделанные им взятки. Но если бы этот другой вистующий был без взяток, он ремиза не ставит.
Игру всегда следует доигрывать до конца и остальные недоигранные карты открывать только тогда, когда взятки действительно неотъемлемы. В противном же случае, т. е. если играющий откроет карты, вистующие этими картами распоряжаются по своему усмотрению. Игрок, вскрывйший карты прежде времени, не может уже взять их снова на руки, и вистующие имеют право заставить его ходить с той карты, с которой они пожелают. После этого, если играющий не сделает законное число взяток, то ставит ремиз и платит за взятки по расчету. И еще: при двух вистах одновременное открытие карт наказывается канделябром.
В противном же случае, т. е. если играющий откроет карты, вистующие этими картами распоряжаются по своему усмотрению. Игрок, вскрывйший карты прежде времени, не может уже взять их снова на руки, и вистующие имеют право заставить его ходить с той карты, с которой они пожелают. После этого, если играющий не сделает законное число взяток, то ставит ремиз и платит за взятки по расчету. И еще: при двух вистах одновременное открытие карт наказывается канделябром.
Прикупивший и назначающий игру должен взять в простых не менее 6 взяток, в семи — 7 взяток, в восьми — 8 взяток, в девяти — 9, в десяти — все десять взяток. Вистующий же или оба обязаны при шестерной игре взять 4 взятки, при семерной — две, при восьмерной тоже две, при девятерной — одну. На игру в десять виста не существует (или по договоренности в некоторых играх можно вистовать), но партнеры имеют право проверять назначавшего. В этом случае карты всех игроков раскладываются на столе и если вистующие каким-нибудь образом докажут, что могут взять взятку, игрок ставит ремиз, а они записывают за вист пополам.
Если игрок, назначавший игру, возьмет законное число взяток — то записывает к себе в пулю стоимость игры. Таблицы стоимости игры помещены ниже.
Вистующим партнерам играющий платит за каждую взятку призы (висты), соответственно игре. Например: если он играл простые черви, то вистующим платит по 2 (Сочи, Ростов) или 4 (Ленинград) за взятку. Эти вистовые записи помещаются отдельно от пули и горы.
Игрок, назначавший игру и не взявший законное число взяток, ставит наверх ремиз в том же размере, какой оы он списал при благоприятных обстоятельствах согласно таблицам расчета.
Вистующий, недобравший взятку, ремиз всегда ставит согласно таблицам расчета.
Когда при назначении игры одним из игроков другие оба пасуют, то назначавший записывает в пулю с игры без разыгрывания.
Если один на объявленную игру пасует, а другой вистует и идет без приглашения, то число обязательных взяток для виста изменяется так: при простой игре — он должен взять только две, при игре семь, восемь и девять — одну. Впрочем, на игру восемь и девять никогда один без приглашения никто не вистует.
Впрочем, на игру восемь и девять никогда один без приглашения никто не вистует.
Пасующий имеет право, если его вистующий не приглашает, сам, пригласить его. Тот обязан по желанию пригласившего или открыть карты или идти в темную.
Если один из играющих запишет в пулю установленное количество раньше других, то в последующие игры он записывает вистующим й графе взятую сумму.
Выиграть игру без козырей можно при своем первом ходе, с такими картами: если есть одной масти туз, король сам шесть; или туз, король, дама сам пять и еще какой-нибудь туз, вообще шесть верных, неотъемлемых взяток. Еще хороша комбинация карт для бескозырной: король, дама, валет, десятка одной масти и три туза других мастей при фасках. Разумеется, и эти карты для бескозырной годны только для того, кто делает первый выход. При таких картах следует ходить с короля, чтобы отнять от вистующих туза.
Чтобы играть бескозырную за рукою (т. е. не имея первого хода), нужно непременно иметь всех четырех тузов, а при одном из них короля, даму, или двух королей. Разумеется, можно играть бескозырную за рукою, если будет только три туза с двумя королями и король даже той масти, туза которой не имеется.
Разумеется, можно играть бескозырную за рукою, если будет только три туза с двумя королями и король даже той масти, туза которой не имеется.
Вист при бескозырной рискован. Если и вистуют на такую игру, то не иначе как с приглашением в открытую. Особенно опасен вист при условии первого выхода назначившим.
Для бескозырного виста нужно иметь по крайней мере: двух тузов, или туза и короля, или туза в одной масти, а короля и даму другой.
Консоляцией называется та плата, которую получая четвертый сдающий игрок или вистуюцие, когда они обремизирывают играющего. За каждую недобранную взятку пишут согласно таблицам расчетов.
За обремизившимся вистующим сдатчик не записывает ничего.
За проданного туза (т. е. если в прикупе таковой окажется) сдатчик записывает висты по договоренности, а за проданных туза и короля одной масти — в два раза больше, и за двух тузов — в три раза больше (обычно в Ростове).
Когда все три игрока пасуют, то разыгрывается распасовка. При игре вчетвером выходит с первой карты прикупа сдающий — все игроки стараются уступить ему эту взятку, но если она уж слишком мала, например, семерка или восьмерка, то взять ее приходится одному из них. Потом сдающий выходит с другой карты и опять игроки стараются уступить взятку друг другу. После того, как сдатчик отходит прикупом, ход игрока, сидящего от него слева. Вся игра продолжается в поддавки.
При игре вчетвером выходит с первой карты прикупа сдающий — все игроки стараются уступить ему эту взятку, но если она уж слишком мала, например, семерка или восьмерка, то взять ее приходится одному из них. Потом сдающий выходит с другой карты и опять игроки стараются уступить взятку друг другу. После того, как сдатчик отходит прикупом, ход игрока, сидящего от него слева. Вся игра продолжается в поддавки.
Игрок, не взявший при распасовке ни одной взятки, списываете с горы или пишет в пулю в зависимости от договоренности. Это относится и к сдатчику, если он не взял взятки.
За каждую взятку, взятую при распасовке, пишется в гору согласно таблицам расчета или пишутся висты (в Ростове).
В распасовочной игре козырей не существует, но ренонсы делать нельзя. На требуемую масть должно давать таковую же, если она имеется, а не сбрасывать другую. Сделавший подобный ренонс ставит по 10 наверх за каждую ошибку.
Распасовка — ничто иное, как проверка сдачи. Она не особенно нравится прижимистым игрокам и тем, которые не прочь иногда подсадеть имеющего хорошие карты и пасующего только для того, чтобы наверное обремизить одного из партнеров, оплошавшего рискованной покупкой.
При распасовке сносить лучше всего на требуемую масть, которой на руках не имеется, старшую карту короткой масти, а длинные масти с большими фигурами и без того отыграются. Например: на руках туз, король и две маленьких пики, король и две маленьких бубны и дама и две маленьких черви, а выход сделан с трефы. На первый раз лучше всего сбросить короля бубен, а на второй даму червей. Если после этого придется делать выход, то самый лучший — в бубну или черву. При постороннем ходе в пику давать маленькие этой масти и можно быть в полной уверенности, что не дадут ни одной взятки, разве только у одного из игроков окажется три пики, но и то навряд, чтобы он додержал их до конца розыгрыша.
При игре втроем в распасовку прикуп открывается или не открывается (в зависимости от договоренности). Первый выход делает игрок, сидящий слева от сдатчика.
К мизерам покупать можно, когда на руках нет ни одной взятки и карты приблизительно такие: туз, сам пять без фигур и все другие маленькие; если при всех фосках имеется валет с семеркой или восьмеркой или дама с одной из таких же карт, то это уже несколько
рискованный мизер и возможен при условии ренонса в какой-либо масти.
Можно прикупать к королю с тремя маленькими (остальные уж, разумеется, должны быть фоски). К валету-десятке и семерке покупать трудно. К королю-даме и семерке прикуп совершенно немыслим, ремиза не избежать ни под каким видом.
Туз, восьмерка и семерка — мизер неверный, но при тузе-десятка, восьмерка и семерка — мизер почти беспроигрышный, потому что трудно себе представить четыре карты одной масти у одного из вистующих.
Очень небезопасно играть мизер при короле, девятке и восьмерке, а также при десятке-восьмерке сам друг.
Играющий мизер никогда не должен перекрывать взятку.
Уклоняться от этого правила можно только тогда, когда какая-нибудь масть распложена так, что четыре карты этой масти, при восьмерке и десятке, нохдятся у играющего мизер, а другие четыре той же масти при семерке и девятке, находятся в руках одного из вистующих, и он выходит с семерки, то для избежания двух ремизов, которые могут быть наверное (если семерку перекрыть восьмеркой, то девятку обязательно придется взять десяткой), следует семерку перекрыть самой старшей картой той же масти, и ходить уже с другой безопасной.
Вистующие на мизере обязаны отвечать друг другу, в особенности же тогда, когда один из них открывает ренонс, на который хочет сбросить старшие карты другой масти, в которой играющий мизер может быть пойман.
Если один из вистующих сделает ренонс, а играющий мизер обремизится, то по проверке факта, играющий списывает с игры как бы за сыгранный мизер, а провинившийся ставит следуемую курочку за каждую взятку, взятую игроком.
С той масти, которой у играющего по первому ходу неоказалось ходить более не следует, дабы он не снес опасной для него карты.
После четвертого или пятого хода вистующим нетрудно заметить опасную масть для играющего мизер и тогда им следует проводить эту масть.
В игре с мизером вистующие должны быть очень внимательны и строго следить за переговорами и за сбрасываемыми картами, потому что малейший промах вистующего спасает от ремиза играющего.
Вистующим на мизере обязательно нужно приглашать партнера, т. е. играть в открытую.
При игре мизер за взятки и консоляции не платят. Также и сдатчик за проданных тузов для мизерной игры ничего не записывает.
Также и сдатчик за проданных тузов для мизерной игры ничего не записывает.
Взятки все могут быть рассматриваемы как играющим, так и вистующими.
Вистующие при сносе, т. е. сбрасывая карты на козырей или на ту масть, которой не имеется и козырями бить нельзя, должны придерживаться правила: при первом сносе сбросить карту той масти, которая у них самая лучшая и сильная, а потом могут сбрасывать любые. Это называется показать масть товарищу. Во-первых, поэтому он не станет беречь этой масти и без затруднения будет сносить ее, а во-вторых он будет знать, во что ходить при заручке. Если вистующие не станут этим руководствоваться, будут постоянно в ремизе.
Масть, которая, по предположению, должна быть у играющего, не может быть сбрасываема, а должна беречься до конца.
Оба вистующие одинаковую масть не сносят. Каждый сбрасывает масть, показанную товарищем. Так, если первый вистующий сбросил трефу и указал этим, что трефа у него масть сильная, второй сбрасывает все время трефу, предварительно, впрочем, сбросив черву, показав ее своею мастью. Тогда первый станет все время сносить черву.
Тогда первый станет все время сносить черву.
Так же оба вистующие сбрасывают масть, которую играющий бьет козырем. Впрочем смотря по игре и по картам, одну или две таковых приберегает для того, чтобы пойти с нее под козыря.
Преферанс является классической карточной игрой, которая родилась в России в XIX веке. По сложности и увлекательности она похожа на шахматы. Потому она ценилась аристократами. Увлечены ею были писатели, музыканты, художники. В настоящее время с каждым днем растет численность людей, которые заинтересовываются преферансом. Для них это является занимательным хобби. В целом довольно интересный преферанс. Правила игры здесь являются своеобразными. Об этом далее подробнее.
Права и обязанности сдающего
В этом плане имеется немало нюансов. От того, кто сдает карты, не зависит, что попадет в прикуп. Но значение игральных карт влияет на его вознаграждение или наказание. Если участника прикуп не устраивает и он возвращает его сдающему, то тот наказывается штрафными очками в гору. Количество их зависит от того, какая игра была заказана. Это важно знать. Премиальные очки или висты тоже зависят от заказанной игры. Сдающему причитаются:
Количество их зависит от того, какая игра была заказана. Это важно знать. Премиальные очки или висты тоже зависят от заказанной игры. Сдающему причитаются:
- За туза в прикупе висты, равные одной взятке. Она соответствует заказанной игре.
- За даму и короля одной масти висты, в размере одной взятки. Данная комбинация игральных карт называется «марьяж».
- За туза с королем одной масти висты, равные двум взяткам.
- За двух тузов также причитаются определенные очки. Они такие, как за три взятки.
- За несыгранный заказ следует наказание «за подсад».
Сдающий может участвовать в заказе под названием «мизер». Это когда нельзя брать взяток вообще. Если его пригласит играющий в эту игру партнер. Так бывает, когда карты для «мизера» сданы не очень удачные, но есть надежда, что в прикупе подходящие. Хотя, возможно, это и не так. Все зависит от случая. Проигрыш тогда расписывается на двоих. Однако и победные очки тоже делятся пополам. Это для сдающего очень привлекательно в приглашении на мизер. Если он согласен играть, то ему дают ознакомиться с раскладом карт заказчика.
Если он согласен играть, то ему дают ознакомиться с раскладом карт заказчика.
Сдающий обязан следить, чтобы прикуп не засветился до конца торга. Также и сам он не должен смотреть его. Особое значение имеет то, когда сдающего приглашают играть «пополам». Это важно помнить.
Классификация
Минимальная игра в преферансе — «шестерик». Это когда участник взять должен определенное количество взяток. А именно шесть. Оставшиеся четыре делят между собой его партнеры. При этом не имеет значения распределение взяток между вистующими: у каждого по две; у одного три и у другого одна; или все в одной руке. В любом случае будет считаться игра сыгранной. Заверенной будет она и тогда, когда участник взял больше взяток, чем обязался. Только в этом случае имеется определенное условие. А именно то, что вистующий, у которого будет взяток меньше двух, записывает себе очки в гору. Это следует помнить. Игра является несыгранной, если у участника оказалось взяток меньше заказанного. В этом случае он штрафуется и ему пишутся очки в гору. А вистующие получают очки за дополнительные взятки и за подсад.
А вистующие получают очки за дополнительные взятки и за подсад.
Дальше следуют игры, названные по числу заказываемых взяток. А именно: «десятерная», «девятерная», «семерная», «восьмерная», или «тотус». Это также важно знать. «Тотус» — это игра, абсолютно противоположная «мизеру». О нем говорилось ранее. Есть еще и наивысшая игра. Но комбинации карт для нее случаются крайне редко. Именно она называется «преферанс». Объявляется она тогда, когда участник после получения прикупа имеет на руках по три карты самого старшего номинала одной масти. Или по четыре самых младших. Это тоже в одной масти.
Довольно жесткими являются условия «шестерной» и «девятерной» вариации в преферанс. Правила игры здесь также следует строго выполнять. То есть вистующие обязательно должны взять заявленные взятки. А именно: четыре при шестерной игре и одну при девятерной. Такие вариации, как «семерик» и «восьмерик», обладают более гибкими правилами. То есть может быть у вистующих определенное количество взяток. Две на седьмой игре и одна на восьмой.
Две на седьмой игре и одна на восьмой.
Раздача карт
В данном случае все довольно-таки просто. Колода карт тасуется сдающим. Это было указано выше. Раздача карт производится парами. То есть трем игрокам по 10 штук и 2 в прикуп. При этом последняя пара карт должна быть средней. А именно не первой и не последней.
Торговля
После ознакомления с картами игроки начинают торговаться за вид игры. Первым заявку вносит участник, сидящий за сдающим по часовой стрелке. Начало торга осуществляется с минимальной игры. А именно «6 пик» и дальше. Каждый игрок заявляет игру выше по масти, чем предыдущий. Или он пасует и выходит из торговли. Игры возрастают от 6 до 10. Старшинство мастей идет в определенном порядке. А именно: пики, трефы, бубны, черви. Старше любой масти игра без козыря. Хотя количество взяток остается такое, какое было заявлено. Объявить «мизер» нельзя в том случае, если игрок уже торговался за другую игру или пасовал. Но это можно перебить заявкой на девятерную игру. Тогда торг прекращается в преферанс. Правила игры еще предусматривают и другие варианты. А именно, когда озвучивается мизер без прикупа, то его можно перебить заявкой на девять. При «пасе» всех участников играют «распасы». Это также следует знать. Если не проводятся «мизер» и «распасы», то участники торгуются до последнего игрока. Далее рассмотрим это более детально.
Тогда торг прекращается в преферанс. Правила игры еще предусматривают и другие варианты. А именно, когда озвучивается мизер без прикупа, то его можно перебить заявкой на девять. При «пасе» всех участников играют «распасы». Это также следует знать. Если не проводятся «мизер» и «распасы», то участники торгуются до последнего игрока. Далее рассмотрим это более детально.
Разновидности игры
Существует три вариации:
- На взятки.
- Мизер.
- Распасы.
Подробное их описание будет изложено ниже.
Игра в карты преферанс на взятки
Здесь имеются определенные условия. То есть, кто выиграл торг, тот обязан играть с заявленным козырем (или без него). Также он должен набрать взяток столько, сколько заказал. Участник, взяв прикуп и сбросив ненужные ему две карты, говорит то, с каким козырем будет играть (или без него). Также он сообщает о том, какое количество взяток он обязуется взять. В данном случае имеется определенное ограничение. Оно заключается в том, что нельзя заказать взяток меньше, чем было заявлено при торге. Например, доторговавшийся до 7 бубен может играть от 7 бубен и выше, 8 пик и т. д. Однако не может 7 пик или 6 другой любой масти. Остальные все играют совместно против него. Однако из них каждый сам решает, вистовать или пасовать. Все зависит от желаний и возможностей участников. Вистующий тоже обязуется взять определенное игрой количество взяток. Если это делают оба партнера, то игра проходит в закрытую. Если же вистующий один, то можно играть в открытую. Тогда оба открывают карты. Вистующий же ходит за двоих. То есть за себя и за того, кто спасовал. Целью игры всегда и для всех является выполнение своих обязательств. То есть нужно собрать оговоренное количество взяток. А также постараться вынудить противника их набрать меньше, чем он заказал. Или же дать как можно больше взяток, если играется мизер. В этом и заключается определенная тактика.
Например, доторговавшийся до 7 бубен может играть от 7 бубен и выше, 8 пик и т. д. Однако не может 7 пик или 6 другой любой масти. Остальные все играют совместно против него. Однако из них каждый сам решает, вистовать или пасовать. Все зависит от желаний и возможностей участников. Вистующий тоже обязуется взять определенное игрой количество взяток. Если это делают оба партнера, то игра проходит в закрытую. Если же вистующий один, то можно играть в открытую. Тогда оба открывают карты. Вистующий же ходит за двоих. То есть за себя и за того, кто спасовал. Целью игры всегда и для всех является выполнение своих обязательств. То есть нужно собрать оговоренное количество взяток. А также постараться вынудить противника их набрать меньше, чем он заказал. Или же дать как можно больше взяток, если играется мизер. В этом и заключается определенная тактика.
Мизер
Это также своеобразный вид. Игра без взяток называется «мизер». Вся суть ее видна по названию. Многие пользуются таким видом, как «мизер». Преферанс в этом плане обладает определенным критерием. То есть оппоненты играют в открытую и без обязательств. Их цель — это всучить противнику как можно больше взяток.
Преферанс в этом плане обладает определенным критерием. То есть оппоненты играют в открытую и без обязательств. Их цель — это всучить противнику как можно больше взяток.
Распасы
В данном случае каждый играет на себя. При этом стараться взять необходимо как можно меньше взяток. Или хотя бы не больше чем партнер. Это является «ростовским» вариантом. Карты прикупа могут определять масть двух первых взяток. Также они могут принадлежать сдающему. Это при игре вчетвером. Или они могут не открываться вовсе («ростов», «гусарик»).
Розыгрыш
Это также следует знать. Очень важно в преферансе разыграть взятку! Игроки в определенном порядке кладут каждый по одной карте. Это понятно. Первая карта задает масть. Далее кладут остальные. То есть карту той же масти. Или же кладут козырную. Это если нужной масти нет. Либо любую другую карту. Это если нет козыря. Забирает взятку игрок, который положил старшую карту. Это определенный факт. Взятки считаются по их количеству. Это независимо от номинала карт.
Счет
За сыгранную игру играющий осуществляет себе запись определенного количества очков в пулю, а вистующий — на него. Превышение обязательства записывается только последним. За каждое нарушение заявки игрокам записывают в гору определенное количество очков. Взятки, полученные на «распасах», тоже заносятся туда же. Или игрок, который их взял меньше всех, проводит запись вистов на других участников («ростов»).
Игры на семь—десять
Рассмотрим данные вариации в преферанс. Правила игры в данном случае довольно просты. Вистующие на «семерной» взять обязаны по одной взятке. Это определенное условие. На «восьмерной» оба вистуют редко. Один обычно говорит: «Пас». Однако он все равно вистует. Хоть за это он не получает никакого вознаграждения. Если оба вистующих спасовали, то они не бросают карты. Они играют безвозмездно. То есть ради проверки соперника. Это называется форсированный вист.
Эта проверочная комбинация обязательна при «девятерной» и «десятерной» играх! В этом случае выигравшему списывается столько, сколько он заказал. А вистующие получают за взятки очки, которые зависят от того, какая игра игралась. «Девятерной» и «десятерная» являются редкими.
А вистующие получают за взятки очки, которые зависят от того, какая игра игралась. «Девятерной» и «десятерная» являются редкими.
«Семерная» или «восьмерная» становится спорной, когда два участника желают играть ее одновременно. Преимущество в данном случае имеет старшая масть.
Бескозырная игра
Здесь само данное название говорит за себя. В этом в преферанс, фото которой предоставлено в данном тексте, заключается в номинале карт. В данном случае козырей не полагается. Бескозырка любую перебивает игру. За нее списывают 60 «пуаней».
Заказывать игру без козырей можно, если у игрока на руках имеется такой набор карт:
Преферанс с поддавками
Множеством хитростей обладает преферанс. Многочисленные разновидности с новыми правилами выработались позже. Например, изначально при трех пасах сдача не засчитывалась. На новую игру колода карт переходила уже к следующему участнику. Это было несправедливо. Так как первый сдающий «терял» руку. А смешанные мгновенно карты скрывали. Ревизия игры не позволялась. Это если кто-то из игроков с хорошими картами не играл, а пасовал в надежде «обремизить» партнеров. Бывают и такие.
Ревизия игры не позволялась. Это если кто-то из игроков с хорошими картами не играл, а пасовал в надежде «обремизить» партнеров. Бывают и такие.
Чтобы предупредить это, придумали определенное условие. А именно: при общих пасах не бросать карты, а играть партию в поддавки. В этом случае выигрывает тот, кто ни одной не взял взятки. Это также важно знать. При этом нужно стараться не взять больше трех взяток. Они подлежат амнистии.
За каждую взятку сверх трех дается по 10 ремизов. За 4 взятки — 10. За 5, соответственно, 20 и т. д. За ренонс — отсутствие на руках какой-либо масти — тоже ставят 10 ремизов. Проверочная игра внушает игрокам некоторую осторожность. Это не всем нравится. Поэтому она не популярна.
Компьютерная версия
Это также занимательная вариация. В настоящее время компьютерная версия преферанса такова, что новички могут быстро освоить определенные правила и играть в режиме онлайн. Для них разработана подробная обучающая справка. Возможна также игра с подсказками. Профессионалы в этой сфере смогут выбрать вариант любой сложности и сильных компьютерных противников. Также в режиме «решатель задач» можно самим составлять расклад карт и разыгрывать партии. Искусственный интеллект в игре таков, что в торгах за прикуп ваши противники себя будут вести в соответствии с тем, кого вы выбрали. Это или осторожные, или рисковые соперники. Плюсами игры является набор присказок, любимых преферансистами. Во время игры постигаются ее тонкости и одновременно карточная «мудрость». Есть подробности расписывания пули, где отражен весь игровой процесс, а также значение Автоматическое подсчитывание выигрыша понравится новичкам. После всего идет раздел «завершение игры». Там же высвечиваются достижения участников.
Профессионалы в этой сфере смогут выбрать вариант любой сложности и сильных компьютерных противников. Также в режиме «решатель задач» можно самим составлять расклад карт и разыгрывать партии. Искусственный интеллект в игре таков, что в торгах за прикуп ваши противники себя будут вести в соответствии с тем, кого вы выбрали. Это или осторожные, или рисковые соперники. Плюсами игры является набор присказок, любимых преферансистами. Во время игры постигаются ее тонкости и одновременно карточная «мудрость». Есть подробности расписывания пули, где отражен весь игровой процесс, а также значение Автоматическое подсчитывание выигрыша понравится новичкам. После всего идет раздел «завершение игры». Там же высвечиваются достижения участников.
Заключение
В целом существуют различные популярные карточные игры. Преферанс является одной из них. Стоит только внимательно ознакомиться с определенными критериями игры. Об этом вы узнаете, ознакомившись с содержанием данного текста.
Инструкция
Игра в преферанс предусматривает несколько вариантов. Так, в эту карточную игру могут играть два или четыре человека, а игра может осуществляться на взятки, распасы или мизер. Ознакомьтесь с правилами игры, внимательно прочитав их в специальной литературе или на любом из информационных ресурсов Сети. Потренируйтесь, проведя «свою» игру от лица двух или четырех игроков, а для этого произведите ряд следующих действий.
Так, в эту карточную игру могут играть два или четыре человека, а игра может осуществляться на взятки, распасы или мизер. Ознакомьтесь с правилами игры, внимательно прочитав их в специальной литературе или на любом из информационных ресурсов Сети. Потренируйтесь, проведя «свою» игру от лица двух или четырех игроков, а для этого произведите ряд следующих действий.
Определите пулю. Это цифра, до достижения которой одним из игроков будет продолжаться игра. Как правило, это цифра 20.Возьмите колоду из 32 карт. При игре в преферанс используются карты от 7 до туза. Учтите, что каждая из мастей имеет свою иерархию. Так, масть пики – первая, трефы идут вторыми, бубны – третьими и червы, соответственно четвертыми.
Возьмите лист бумаги и разметьте его так, как требуют правила. Это пулька, которая используется каждым из участников. Именно в области пульки записываются очки игроков, которые необходимы в последующем для подсчета. Потасуйте колоду карт и раздайте парами (каждый раз по две карты) каждому из мнимых игроков и себе. Карты раздаются по часовой стрелке в порядке очередности, пока общее количество карт у каждого из игроков не достигнет десяти.
Карты раздаются по часовой стрелке в порядке очередности, пока общее количество карт у каждого из игроков не достигнет десяти.
Положите 2 карты в середину. Это будет прикуп. При этом важно знать, что в случае, если играет два человека, в прикуп кладется не последняя и не первая пара карт, а в случае, если в преферанс решили сразиться четверо, в прикуп идет две нижние карты.Переверните карты свои и мнимых игроков и проанализируйте ситуацию.
Сделайте ставки за себя и игроков, за которых вы якобы играете. На этом этапе в реальной игре, после того, как каждый из играющих оценит свои карты, происходит торг. Торг проводится по часовой стрелке от одного играющего к другому. Первый делает ставку тот игрок, который сидит следующим после раздающего. Торг начинается в соответствии с правилами с минимальной игры, то есть с 6 пики. После первой ставки каждый игрок называет свою, которая должна брать выше. В случае, если игрок не делает ставку, он пасует. После этого начинается игра, по которой и будут подсчитываться взятки и соответственно очки.
Игра может быть трех типов — игра на взятки, распасы или мизер. Именно от типа игры и зависит подсчет взяток в последующем.Сыграйте за себя и своих мнимых соперников, делая поочередные ходы в соответствии с правилами игры.Подсчитайте количество набранных очков всех играющих так, как это предусматривают правила игры и запишите эти числа на лист бумаги.
Сыграйте еще несколько раз, чтобы окончательно понять правила преферанса и играть уже не подсматривая в них.Перейдите на игру с компьютером или виртуальными соперниками. Это будет тоже своего рода тренировка, ведь играя за компьютером, так же как и с мнимыми соперниками, вы всегда имеете возможность подсмотреть в правила игры или воспользоваться чьей-то подсказкой.Попробуйте преферанс , полностью освоившись с игрой.
Обратите внимание
Одной из самых популярных игр в России с начала 19 века стал Преферанс. «Распиcать пульку» любили многие известные и выдающиеся поэты, писатели и политические деятели. Сейчас преферанс не менее популярен, и более широко распространён не только в России, но и в странах ближнего зарубежья. Всё больше любителей и ценителей этой карточной игры предпочитают играть в неё по сети Интернет.
Всё больше любителей и ценителей этой карточной игры предпочитают играть в неё по сети Интернет.
Полезный совет
Загрузив и установив игру преферанс на компьютер, вы сможете настроить все игровые моменты в точности с привычными правилами, по которым играют в вашей компании. В результате, игра в компьютерный симулятор преферанса ничем не будет отличаться от настоящей игры в кругу друзей. К основным плюсам компьютерной версии преферанса стоит отнести возможность в любой момент остановить игру и вернуться к ней через время, открыв неоконченную пулю.
Основные правила игры в преферанс
Колода карт для игры в преферанс
Преферансная колода состоит из 32 карт. В ней 4 масти по 8 карт в каждой — от туза до семерки. Старшинство мастей по возрастанию: пики, трефы, бубны, червы.
Старшинство карт в масти по возрастанию: семерка, восьмерка, девятка, десятка, валет, дама, король, туз.
Одна из мастей может быть назначена козырем, тогда любая козырная карта старше любой некозырной. В козырной масти старшинство карт сохраняется.
В козырной масти старшинство карт сохраняется.
Правила взяток и очередность хода в преферансе
Первая карта, положенная на стол, называется ходом. На ход каждый игрок обязан выложить одну карту. Карты выкладываются по следующим правилам:
На ход игрок обязан класть карту масти хода. Если в руке карт масти хода нет, игрок обязан класть козырь. Если нет козыря, можно класть любую карту.
Взятку берет игрок, которому принадлежит старшая карта в данной взятке, учитывая козырей. В преферансе права первой заявки при торговле и первого хода в игре передаются от игрока к игроку. Игрок, имеющий право первого хода и первой заявки в торговле, называется «первая рука». Следующий за ним игрок — «вторая рука» и последний игрок — «третья рука».
Виды игр в преферансе
В преферансе три группы игр — игры на взятки, мизер и распасовка. В играх на взятки игрок обязуется взять не менее заявленного им при торговле количества взяток. Игра может идти с козырем и без козыря. Цель других игроков — помешать ему это сделать — т.е., в свою очередь, взять как можно больше взяток (если возможно).
Цель других игроков — помешать ему это сделать — т.е., в свою очередь, взять как можно больше взяток (если возможно).
Заявив мизер, игрок обязуется не взять ни одной взятки. Другие игроки, напротив, стараются вынудить его взять взятки. В распасовках каждый игрок старается взять как можно меньше взяток.
Возможные заказы игр в преферансе
Игры на взятки и мизер ранжируются следующим образом: минимальное количество взяток, которое можно заказать — 6, максимальное — 10. Последовательность контрактов в торговле по возрастанию старшинства приведена в таблице.
Например, контракт 6¦ означает, что игрок обязуется взять не менее 6 взяток с козырем в трефах. Играть можно без козыря (Б/К), такая игра старше козырной при одинаковом количестве взяток.
Запись в преферансе
Смысл игры в преферанс заключается в том, чтобы, оценив свои карты, заказать и сыграть наиболее выгодный контракт. Результаты игр в преферансе записываются в пулю, на гору и в висты. За сыгранный контракт игрок получает очки в пулю. За заказанный и несыгранный контракт игрок получает штраф на гору. Игроки, оппонирующие играющему, пишут на него за каждую взятую ими взятку висты, а если не взяли необходимое количество взяток — получают штраф в гору.
За сыгранный контракт игрок получает очки в пулю. За заказанный и несыгранный контракт игрок получает штраф на гору. Игроки, оппонирующие играющему, пишут на него за каждую взятую ими взятку висты, а если не взяли необходимое количество взяток — получают штраф в гору.
Игровой протокол записи пули, горы и вистов также называется пуля.
Разновидности преферанса, отличающиеся стоимостью игр и распасов, распределением вистов между игроками, особенностями торговли, называются конвенциями. Наиболее распространенные конвенции это — ленинградка, сочинка и ростов.
Торговля
В каждой сдаче играют три игрока. Раздается по 10 карт. Две оставшиеся карты называются прикупом, и их содержание никому неизвестно до момента окончания торговли.
Цель торговли состоит в том, чтобы получить право на прикуп и заказать наиболее выгодный для себя контракт.
Процесс торговли в преферансе состоит в следующем. Каждый игрок, по очереди, по часовой стрелке, может сделать заявку на игру или отказаться от игры. При заявке на игру он должен явно указать тип игры, а при отказе от игры — заявить «пас». Спасовавший игрок в дальнейшей торговле участия не принимает. В свою очередь можно сделать только одну заявку. Минимальный заказ — шесть взяток, с пикой в козырях — т.е. «6 пик». Следующий игрок может заказать в соответствии со старшинством игр в таблице только более старшую игру, то есть «6 треф». Последующей заявкой может быть только «6 бубен» и т.д. Если игрок не хочет торговаться дальше, он может в свою очередь заявить «пас». Последний неспасовавший игрок, участвовавший в торговле и сделавший самую старшую заявку, получает право на прикуп и заказ контракта.
При заявке на игру он должен явно указать тип игры, а при отказе от игры — заявить «пас». Спасовавший игрок в дальнейшей торговле участия не принимает. В свою очередь можно сделать только одну заявку. Минимальный заказ — шесть взяток, с пикой в козырях — т.е. «6 пик». Следующий игрок может заказать в соответствии со старшинством игр в таблице только более старшую игру, то есть «6 треф». Последующей заявкой может быть только «6 бубен» и т.д. Если игрок не хочет торговаться дальше, он может в свою очередь заявить «пас». Последний неспасовавший игрок, участвовавший в торговле и сделавший самую старшую заявку, получает право на прикуп и заказ контракта.
Если спасовали все три игрока, разыгрывается распасовка — игра, в которой все стараются взять как можно меньше взяток.
Заказ игры
После окончания торговли прикуп открывается на всеобщее обозрение и отдается игроку, выигравшему право на заказ игры. Игрок берет прикуп и сносит две любые карты в снос. После этого он должен заказать игру. Заказывать можно любую игру не младше той, на которой остановилась торговля. Есть одно исключение — мизер. Заказывать мизер можно только сразу. То есть, нельзя сначала сказать «шесть пик», а потом, на следующем круге торгов — «мизер». Если игрок взял прикуп, то заказывать игру обязательно, даже если ее заведомо невозможно выиграть.
Заказывать можно любую игру не младше той, на которой остановилась торговля. Есть одно исключение — мизер. Заказывать мизер можно только сразу. То есть, нельзя сначала сказать «шесть пик», а потом, на следующем круге торгов — «мизер». Если игрок взял прикуп, то заказывать игру обязательно, даже если ее заведомо невозможно выиграть.
Игра на взятки
Игрок, участвовавший в торговле и взявший прикуп, обязан заказать игру не ниже той, до которой дошла торговля. Например, если торговались до 7 пик, то шестерные игры заказать уже нельзя. Игра назначается после сноса.
Заказав игру, играющий обязуется взять определенное количество взяток. Если играющий не набирает нужного числа взяток, ему записывается штраф на гору. Величина штрафа зависит от недобранного количества взяток. Недобор взяток называется ремиз.
Если играющий берет заявленное число взяток, делается запись в пулю, в размере, определенном для данной игры.
Если играющий взял больше взяток, чем требовалось по заказанной игре — например, заказал 6 взяток, а взял 7 — запись все равно идет в соответствии с заказанной игрой.
Игра на взятки разыгрывается, если она завистована. Это означает, что хотя бы один из соперников по игре заявил «вист» и, таким образом, принял на себя обязательство взять определенное количество взяток. Если все игроки сказали «пас», то игра считается сыгранной, и в пулю делаются соответствующие записи.
Вист
После того, как произошел заказ контракта, остальные игроки должны определиться — обязуются ли они взять положенное им в данной игре число взяток, или нет. Если игрок обязуется взять определенное число взяток, он заявляет «вист», если нет — «пас».
Вистовать — разыгрывать контракт — можно втемную и всветлую. Если вистуют оба игрока, то вист всегда втемную. Если вистует один игрок, а другой пасует, то вистующий игрок выбирает тип виста — всветлую или втемную. Если выбран вист всветлую, то карты и пасующего и вистующего игрока выкладываются на стол, и вистующий распоряжается как своими картами, так и картами спасовавшего.
Если право первого хода у играющего, то игроки должны перед началом игры договориться, в какой момент открывать карты — до первого хода или после первого хода играющего.
Ответственность при вистовании
Если игра завистована, то вистующий несет ответственность за взятие определенного числа взяток (см. таблицу). Пасующий такой ответственности не несет.
За каждую взятку вистующий пишет определенное число очков (вистов) на играющего.
Если вистуют оба соперника играющего, то, при недоборе взяток (ремизе), кроме вистов за фактические взятки, игрок, недобравший взяток пишет штраф в гору.
На восьмериках, девятериках и тотусах (десятерных играх) ответственность за недобор взяток несет игрок, вистовавший вторым (по договоренности ответственность может быть разделена между вистующими).
Если играющий недобрал взяток, то вистовавшие дополнительно к вистам за фактические взятки, получают консоляцию — премию за подсад играющего.
Размер консоляции, ее распределение между игроками, количество очков за взятку — зависит от конвенций преферанса.
Если сидящий по часовой стрелке за играющим игрок заявил «пас», то следующий может сказать «полвиста».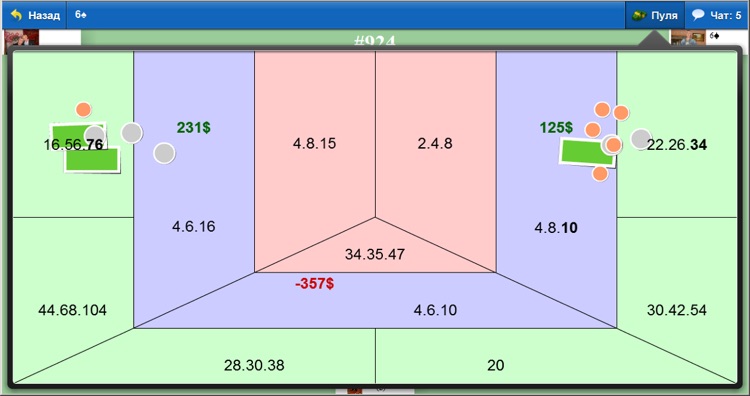 Это означает, что он без игры соглашается на половинную норму вистов, и игра считается сыгранной. Для шестерной игры «полвиста» — 2 взятки, для семерной — 1 взятка. После того, как партнер сказал «полвиста», пасовавший партнер имеет право вернуть вист, сказав «вист». Если игра идет вчетвером, вернуть вист может также и четвертый игрок. Если один игрок сказал «пас», другой сказал «полвиста», первый снова сказал «пас» — четвертый игрок имеет право посмотреть карты у одного из двух игроков и вернуть вист. Если вист возвращен, то партнер, уходивший за полвиста, теряет право на вист и обязан сказать «пас».
Это означает, что он без игры соглашается на половинную норму вистов, и игра считается сыгранной. Для шестерной игры «полвиста» — 2 взятки, для семерной — 1 взятка. После того, как партнер сказал «полвиста», пасовавший партнер имеет право вернуть вист, сказав «вист». Если игра идет вчетвером, вернуть вист может также и четвертый игрок. Если один игрок сказал «пас», другой сказал «полвиста», первый снова сказал «пас» — четвертый игрок имеет право посмотреть карты у одного из двух игроков и вернуть вист. Если вист возвращен, то партнер, уходивший за полвиста, теряет право на вист и обязан сказать «пас».
На восьмерной и девятерной второй игрок не может уйти за полвиста. Четвертый игрок может вистовать на картах только одного из спасовавших игроков.
Мизер
Мизер — игра, когда играющий обязуется не взять ни одной взятки.
Мизер можно заказать только в случае, если игрок в текущей сдаче не сделал до этого ни одной заявки.
В торговле мизер перебивается девятерной (или, по договоренности, десятерной игрой).
Мизер играется без козырей, все остальные правила взяток (берет старшая карта, на масть обязательно класть масть, если нет масти, класть можно любую карту, ходит игрок, взявший последнюю взятку) сохраняются.
Распасовка, или распасы
Распасовка разыгрывается, если все три игрока заявили «пас». Распасовка — это игра, при которой все игроки стараются взять как можно меньше взяток.
Козырей на распасовке нет.
Игра начинается с того, что последовательно открываются по одной карты прикупа.
При игре втроем карта прикупа только обозначает масть, а взятка принадлежит тому из игроков, кто положил старшую карту.
При игре вчетвером, карта прикупа принадлежит четвертому игроку. Поэтому если эта карта берет взятку, то это взятка считается сдатчику и записывается в гору на общих основаниях.
В Ростовской разновидности преферанса карты прикупа не открываются.
В разных конвенциях преферанса — свои особенности игры и записи результатов распасовки.
Кроме того, игроки могут договариваться перед началом игры о следующих особенностях:
прогрессирующая распасовка — стоимость взятки увеличивается, если играется несколько сдач распасовок подряд. Разновидности прогрессии (арифметическая, геометрическая) и предел прогрессии тоже оговариваются заранее.
Разновидности прогрессии (арифметическая, геометрическая) и предел прогрессии тоже оговариваются заранее.
Выход из распасовки — какая сыгранная игра прерывает распасовки. Выход может быть шестерной (любая сыгранная шестерная игра), семерной и восьмерной.
Стоимость игр
Каждой игре соответствует определенное количество очков, которое игрок записывает или в пулю, если успешно сыграл игру, или на гору, если не взял нужного числа взяток. За каждую взятку при вистовании игрок пишет висты. Если вистовавший игрок недобрал взяток, то он пишет одновременно и висты, и штраф в гору. При ремизе играющего вистовавший игрок пишет консоляцию — премию за подсад игравшего. Размер премии за подсад, распределение вистов, их величина, стоимость игр варьируется в зависимости от разновидности (конвенции) преферанса. В результате всех записей для каждой игры получается баланс выигранных и проигранных вистов, что составляет ее стоимость.
Кодекс Преферанса
Здесь приведены лишь основные правила русского преферанса. Полностью правила изложены в Кодексе Преферанса.
Полностью правила изложены в Кодексе Преферанса.
Читать «Русский преферанс» — Лесной Дмитрий Станиславович «Dima» — Страница 128
«Прикуп в морду». Подсчёт вероятных выгод
В некоторых компаниях применяется правило, по которому разыгрывающий может отказаться от прикупа — «бросить прикуп в морду» сдающему, который в этом случае пишет в гору единичку или двоечку, а иногда — и всю стоимость заказанной игры.[184] Кодекс преферанса[185] допускает отказ от прикупа, но не рекомендует использовать это правило в турнирах: «Отказ от прикупа, по договорённости между игроками, может сулить наказание сдающему в виде условленного количества очков в гору. Однако для серьёзной игры (особенно в квалификационном турнире) это правило применять нежелательно: никто не должен страдать из-за неумения класть в прикуп тузы» (правило 3.4.10). Общего согласия по этому вопросу, однако, нет, и он до сих пор дискутируется между членами редакционной коллегии Общества любителей преферанса. Существует мнение, что отказ от прикупа может являться одним из методов борьбы и, следовательно, правило должно применяться.
По поводу взятки из прикупа Кодекс преферанса гласит: «За взятку, данную разыгрывающему в прикупе, сдающий, по договоренности между игроками, пишет на разыгрывающего консоляцию (премию, компенсацию) как за взятку на заказанной игре. За туза — как за одну взятку; за туза и короля одной масти — как за две взятки; за двух тузов — как за три взятки; за марьяж — как за одну взятку. Однако в серьёзной игре (особенно в квалификационном турнире) это правило, как и правило 3.4.10, применять нежелательно: умение класть в прикуп тузы не должно вознаграждаться» (правило 3.4.11).
Как бы то ни было, решение проблемы, если правило применяется, основывается исключительно на теории вероятностей.
Явно не гусарская игра преферанс! Иногда приходится считать такие досадные мелочи! Словно купчишка в лавке. И тем не менее… Если хотите достичь сияющих вершин, стоит задумываться и о мелочах. Например, о том, «бросить прикуп в морду» или не бросать вот в такой ситуации — сидя на первой руке, вы получаете такую карту:
Вы заявляете мизер и прикупаете туза с восьмёркой червей. По договорённости в этой компании игрок может отказаться от прикупа. В этом случае сдающий пишет единицу в гору. Как поступили бы вы? «Бросите ли прикуп в морду» или оставите себе?
По договорённости в этой компании игрок может отказаться от прикупа. В этом случае сдающий пишет единицу в гору. Как поступили бы вы? «Бросите ли прикуп в морду» или оставите себе?
Давайте сначала посмотрим, что сносить и чем ходить лучше всего (безотносительно наказания сдающему). Ведь наша задача всё-таки не заклеить физиономию сдающего разными картами, а выиграть мизер! Поэтому пусть наше решение будет подчинено единственно целесообразности, т. е., попросту говоря, собственной выгоде.
Если бы ход был чужой, мы бы не задумывались ни на минуту и «бросили бы прикуп в морду» — с размаху и даже не открывая: наш мизер при чужом ходе чист, как слеза ребёнка, при любом прикупе. Но ход наш, и не всё так безоблачно, как хотелось бы. Будут ли взятки — определится уже на первом ходу, поэтому нам нужно выбрать лучший первый ход, т. е. такой, который даст нам взятку с наименьшей вероятностью. Выбор у нас такой: либо с девятки в одной из чёрных мастей, либо с семёрки из-под короля, либо с прикупленной восьмёрки.
1. Ход с любой из чёрных девяток чреват взяткой при раскладе этой масти 5:0. Вероятность такого расклада — 0,0325.
2. Пойдя из-под бубнового короля, вы можете получить на него взятку при раскладе бубны 4:0. Вероятность такого расклада — 0,0867.
3. Восьмёрка червей получит взятку в случае расклада червы 6:0. Вероятность такого расклада — 0,0108.
Из рассмотрения вероятностей следует, что лучше всего оставить червовую восьмёрку и ходить с неё. Ну а как же удовольствие от «бросания прикупа в морду» партнёру и выгода от его записи в гору? В каком соотношении эти два приятных элемента находятся с только что рассмотренными процентами? Давайте представим, что такая ситуация случится 10000 раз. Тогда, в соответствии с теорией вероятностей, при разных выходах и сносах вы получите такие результаты:
| Выход | Чистый | Ловленый | Выигрыш | Проигрыш | Баланс | Мат. ожидание ожидание |
|---|---|---|---|---|---|---|
| ♠9/♣9 | 9675 | 325 | 725625 | 24375 | +701250 | +70,125 |
| ♦7 | 9133 | 867 | 684975 | 65025 | +619950 | +61,995 |
| ♥8 | 9892 | 108 | 741900 | 8100 | +733800 | +73,380 |
(Выигрыш и проигрыш на мизере составляет 75 вистов. )
)
С «единички» в горе партнёра, которую он запишет за то, что вы отказались от его прикупа, вы выигрываете 2,5 виста (при игре вчетвером). Если вы 10000 раз откажетесь от прикупа, вы получите в сумме 25000 вистов прибыли от этой операции. Разница же между выигрышем при ходе в девятку пик и восьмёрку червей составляет 733800-701250=32550. Так что, если вы просто хотите выигрывать, то вам не стоит в этой ситуации «бросать прикуп в морду», а если вы хотите досадить партнёру, то вы лучше всего это сделаете, если выиграете у него.
Вот ещё один пример на тему: «прикуп в морду».
Вы говорите раз на первой руке, имея следующую карту:
— AKQ A7 AKQJ7.Прикупаете туза и короля пик. По правилам компании, в которой вы играете, прикуп можно «бросить в морду» сдававшему (за это он пишет единицу в гору), а за очевидные взятки, прикупленные к игре, сдатчик пишет висты на разыгрывающего. Каковы ваши действия: что снесёте? что закажете?
Ответ даёт таблица стоимостей всех игр. Десятерная игра стоит 75 вистов (в «сочинку» вчетвером). Девятерная — 52 (при условии, что завистуют и возьмут взятку). Теперь добавим условия, поставленные прикупом. Если возьмём прикуп и закажем 10, то выиграем 55 вистов (сдатчик запишет 20 вистов за AK). Если откажемся от прикупа и закажем 9, выиграем 54,5 виста (с единички в горе сдатчика нам достанется четвёртая часть). Поэтому статистически вроде бы нужно брать прикуп и играть 10. К тому же есть вероятность, что кто-либо из партнёров завистует и сядет (в компанию иногда забредают женихи и студенты). С другой стороны, есть вероятность, что не завистуют на девятерной после «бросания в морду». Думается, что она заведомо окупает указанные 0,5 виста. Играем 9 (это лучше, чем 9 без козырей). Есть ещё один план, который с достаточными основаниями может быть назван «аферистическим», — небрежно «бросить прикуп в морду» и заказать… 10 без козыря. Этот план имеет тот недостаток, что карта разыгрывающего может быть просчитана одним из вистующих, которому необходимо иметь три червы, четвёртого валета треф, второго короля бубён и даму пик.
Десятерная игра стоит 75 вистов (в «сочинку» вчетвером). Девятерная — 52 (при условии, что завистуют и возьмут взятку). Теперь добавим условия, поставленные прикупом. Если возьмём прикуп и закажем 10, то выиграем 55 вистов (сдатчик запишет 20 вистов за AK). Если откажемся от прикупа и закажем 9, выиграем 54,5 виста (с единички в горе сдатчика нам достанется четвёртая часть). Поэтому статистически вроде бы нужно брать прикуп и играть 10. К тому же есть вероятность, что кто-либо из партнёров завистует и сядет (в компанию иногда забредают женихи и студенты). С другой стороны, есть вероятность, что не завистуют на девятерной после «бросания в морду». Думается, что она заведомо окупает указанные 0,5 виста. Играем 9 (это лучше, чем 9 без козырей). Есть ещё один план, который с достаточными основаниями может быть назван «аферистическим», — небрежно «бросить прикуп в морду» и заказать… 10 без козыря. Этот план имеет тот недостаток, что карта разыгрывающего может быть просчитана одним из вистующих, которому необходимо иметь три червы, четвёртого валета треф, второго короля бубён и даму пик. Нужно заметить, что рука догадливого вистующего должна с точностью до одной карты совпадать с описанной выше, иначе просчитать руку разыгрывающего невозможно. Но мы с вами должны отвергнуть этот план (и не только потому, что мы помним о женихах и студентах), а по одной только неприязни к афёре. К тому же справа за столом сидит сдатчик с прилипшим к лицу роскошным прикупом… И этот сдатчик, судя по взгляду, готов вернуть вист на любой карте…
Нужно заметить, что рука догадливого вистующего должна с точностью до одной карты совпадать с описанной выше, иначе просчитать руку разыгрывающего невозможно. Но мы с вами должны отвергнуть этот план (и не только потому, что мы помним о женихах и студентах), а по одной только неприязни к афёре. К тому же справа за столом сидит сдатчик с прилипшим к лицу роскошным прикупом… И этот сдатчик, судя по взгляду, готов вернуть вист на любой карте…
(PDF) Характеристики методов подсчета баллов для агрегирования предпочтений
[34] P.C. Фишберн, Суммирование функций социального выбора, Econometrica 41 (1973) 1183–1196.
[35] P.C. Фишберн, Аксиомы для одобрения голосования: Прямое доказательство, J. Econ. Теория 19 (1978) 180–185.
[36] P.C. Фишберн, Симметричное и последовательное агрегирование с дихотомическим голосованием, в: Aggregation
and Revelation of Preferences, ed. Ж.-Ж. Лаффонт, Северная Голландия, Амстердам, 1979, стр. 201–218.
[37] P.C. Фишберн, Об утилитарной теореме кардинального благополучия Харшаньи, Теория и решение 17 (1984)
Фишберн, Об утилитарной теореме кардинального благополучия Харшаньи, Теория и решение 17 (1984)
21–28.
[38] P.C. Фишберн, Межпрофильные условия и невозможность, Основы чистой и прикладной экономики —
nomics, Vol. 18, Harwood Academic, Chur, 1987.
[39] P.C. Фишберн и У. Герляйн, правило Борды, позиционное голосование и принцип простого большинства Кондорсе
, Public Choice 28 (1976) 79–88.
[40] М. Флеминг, Кардинальная концепция благосостояния, Quarterly J.экономики 66 (1952) 366–384.
[41] Дж. М. Флеминг, Кардинальное благосостояние и индивидуалистическая этика: комментарий, J. Polit. Экономика 65 (1957)
355–357.
[42] П. Гарденфорс, Позиционалистские функции голосования, Теория и решение 4 (1973) 1-24.
[43] Л.А. Гудман и Х. Марковиц, Функции социального обеспечения на основе индивидуальных рейтингов, Amer. J.
Sociol. 58 (1952) 257–262.
[44] Х. Гулликсен, Решение методом наименьших квадратов для парных сравнений с неполными данными, Психометрика
21 (1956) 125–134.
[45] Б. Ханссон и Х. Сальквист, Метод доказательства социального выбора с переменным электоратом, J. Econ.
Теория 13 (1976) 193–200.
[46] JC Harsanyi, Кардинальное благосостояние, индивидуалистическая этика и межличностные сравнения полезности, J.
Polit. Экономика 63 (1955) 309–321.
[47] Дж. К. Харсани, Нелинейные функции социального обеспечения, Теория и решение 6 (1975) 311–332.
[48] Дж. К. Харсани, Мораль и теория рационального поведения, в: Утилитаризм и не только, ред.
А. Сен и Б. Уильямс, Cambridge University Press, Кембридж, 1982, стр. 39–62.
[49] Д. Генриет, Функция выбора Коупленда: аксиоматическая характеристика, Soc. Выбор благосостояния 2 (1985)
49–63.
[50] Л. Кац, Новый индекс статуса, полученный на основе социометрического анализа, Психометрика 18 (1953) 39–43.
[51] Р.Л. Кини, Аксиоматизация групповых предпочтений с кардинальной полезностью, Наука управления. 23 (1976)
140–145.
[52] A.B. Хмельницкая, Проблемы социального выбора с разными шкалами измерения индивидуального благосостояния —
для разных подгрупп людей, в: Operation Research Proceedings, Springer, Berlin,
1995, стр.252–257.
[53] Ж.-Ф. Ласлиер, Турнирные решения и голосование большинством, Springer, Berlin, 1997.
[54] RD Luce и H. Raiffa, Games and Decisions: Introduction and Critical Review, Wiley, New
York, 1957.
[55] T Марчант, Агрегация стоимостных отношений с помощью метода Борда, J. Multi-Crit. Decis. Анальный.
5 (1996) 127–132.
[56] Т. Марчант, Кардинальность и оценка Борды, Документ для обсуждения MG 96/9, Université Libre de
Bruxelles, 1996.
[57] Дж. Маршак, Рациональное поведение, неопределенные перспективы и измеримые полезности, Econometrica 18
(1950) 111–141.
[58] Э. Маскин, Теорема об утилитаризме, Rev. Econ. Исследования 45 (1978) 93–96.
[59] В. Мерлин, Некоторые свойства процедур последовательной оценки социального выбора, Препринт, Университет
Кан, 1994.
[60] В. Мерлин, Методы подсчета баллов согласованы, Препринт, Университет Кан, 1996
[61] JWМилнор, Игры против природы, в: Процессы принятия решений, ред. R.M. Тралл, Ч. Кумбс и
Р.Л. Дэвис, Вили, Нью-Йорк, 1954, стр. 49–60.
[61a] П. Монгин, Теорема агрегирования Харшаньи: многопрофильная версия и нерешенные вопросы, Soc.
Choice Welfare 11 (1994) 331–354.
П.Ю. Чеботарев, Э. Шамис
и
Характеристики скоринговых методов 331
Характеристики скоринговых методов для агрегирования предпочтений
C.д’Аспремон, Аксиомы для порядка социального обеспечения, в: Социальные цели и социальные организации: Очерки памяти Элизы Пазнер , ред. Л. Гурвич, Д. Шмейдлер и Х. Зонненшайн, Cambridge University Press, Кембридж, 1985, стр. 19–76.
К. д’Аспремон и Л. Геверс, Справедливость и информационная основа коллектива. выбор, преподобный экон. Исследования 44 (1977) 199–209.
Google ученый
Н.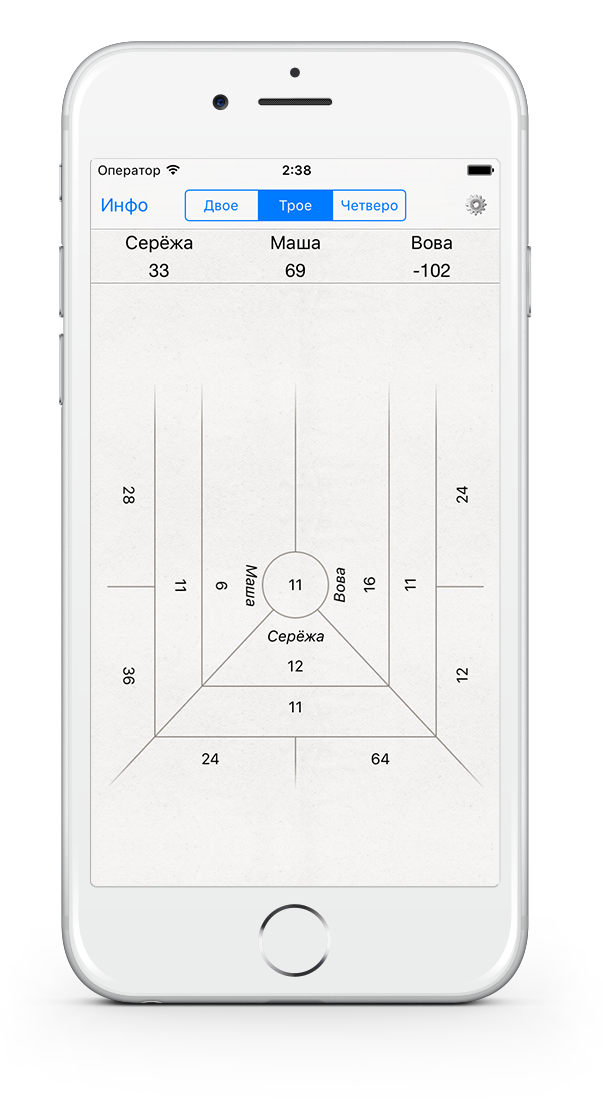 Байгент и Ю. Сюй, Независимые необходимые и достаточные условия для утверждения голосования, Матем. Soc. Sci. 21 (1991) 21 — 29.
Байгент и Ю. Сюй, Независимые необходимые и достаточные условия для утверждения голосования, Матем. Soc. Sci. 21 (1991) 21 — 29.
Google ученый
С. Барбера, Мажоритарное и позиционное голосование в вероятностной структуре, Rev. Econ. Исследования 46 (1979) 379–389.
Google ученый
Дж. Барзилай, У. Д. Кук и Б. Голани, Согласованные веса для матриц суждений об относительной важности альтернатив, Опер.Res. Lett. 6 (1987) 131 — 134.
Google ученый
Дж. Барзилай и Б. Голани, Получение весов из матриц парных сравнений: аддитивный случай, Опер. Res. Lett. 9 (1990) 407 — 410.
Google ученый
Д. Блэк, Теория комитетов и выборов , Cambridge University Press, Кембридж, 1958.
Google ученый
D. Блэк, Частичное обоснование подсчета Борда, Public Choice 28 (1976) 1–16.
Блэк, Частичное обоснование подсчета Борда, Public Choice 28 (1976) 1–16.
Google ученый
Д. Блэквелл, М.А. Гиршик, Теория игр и статистические решения , Wiley, New York, 1954.
Google ученый
В. Боссерт и Дж. Веймарк, Полезность в социальном выборе, в: Справочник по теории полезности , ред. С. Барбера, П.Появятся Дж. Хаммонд и К. Зайдл, Клувер.
D. Bouyssou, Методы ранжирования на основе отношений ценностных предпочтений: характеристика метода чистых потоков, Eur. J. Oper. Res. 60 (1992) 61 — 67.
Google ученый
D. Bouyssou, Заметка о функции выбора суммы разностей для нечетких отношений предпочтения, Системы нечетких множеств 47 (1992) 197–202.
Google ученый
D.Буиссу и П. Перни, Методы ранжирования для отношений оцененных предпочтений: характеристика метода, основанного на исходящих и входящих потоках, Eur. J. Oper. Res. 61 (1992) 186 — 194.
J. Oper. Res. 61 (1992) 186 — 194.
Google ученый
Дж.Р. Чемберлин и П.Н. Курант, Представительские обсуждения и представительные решения: Пропорциональное представительство и правило Борда, амер. Полит. Sci. Обзор 77 (1983) 718 — 733.
Google ученый
П.Ю. Чеботарев, Обобщение метода строчной суммы для неполных парных сравнений, Автоматизация и дистанционное управление 50 (1989) 1103 — 1113
Google ученый
П.Ю. Чеботарев, Метод сумм строк и модели на его основе, Труды Всесоюзного института системных исследований, № 3 (1989) 94 — 110.
Google ученый
П.Ю. Чеботарев, О некоторых методах оптимизации агрегирования предпочтений, Труды Всесоюзного института системных исследований, № 8 (1990) 67 — 72.
П. Ю. Чеботарев, Агрегация предпочтений методом обобщенной строчной суммы, Матем. Soc. Sci. 27 (1994) 293 — 320.
Ю. Чеботарев, Агрегация предпочтений методом обобщенной строчной суммы, Матем. Soc. Sci. 27 (1994) 293 — 320.
Google ученый
П.Ю. Чеботарев и Э. Шамис, Слияние предпочтений, когда количество альтернатив превышает две: процедуры косвенной оценки, в: Труды семинара по основам информации / ecision Fusion , ред.Н.С.В. Рао, В. Протопопеску, Дж. Бернен и Г. Ситхараман, Acadiana, Lafayette, LA, 1996, стр. 20–32.
P. Yu. Чеботарев и Э. Шамис, Неполные предпочтения и косвенные оценки, Документ для обсуждения № 365.97, Departament d’Economia i d’Historia Economica, Universitat Autonoma de Barcelona и Institut d’Analisi Economica, CSIC, Барселона, 1997.
Google ученый
П.Ю. Чеботарев и Э.Шамис, Построение целевой функции для агрегирования неполных предпочтений, в: Построение скалярных целевых функций , ред. A. Tangian и J. Gruber, Springer, Berlin, 1997, стр. 100–124.
Gruber, Springer, Berlin, 1997, стр. 100–124.
Google ученый
У.Д. Кук, Л.М. Сейфорд, О методе консенсуса Борда-Кендалла для проблем ранжирования приоритетов, Management Sci. 28 (1982) 621 — 637.
Google ученый
A.Х. Коупленд, «Разумная» функция социального обеспечения , Семинар Мичиганского университета по применению математики в социальных науках, Мичиганский университет, Анн-Арбор, 1951.
Google ученый
П. Кафлин, Прямая характеристика первого подсчета Борда Блэком, Econ. Lett. 4 (1979) 131 — 134.
Google ученый
D.J. Кауден, Метод оценки участников, Американский статистик 29, No.2 (1975) 82 — 84.
Google ученый
H.E. Дэниелс, Результаты круговых турниров, Биометрика 56 (1969) 295 — 299.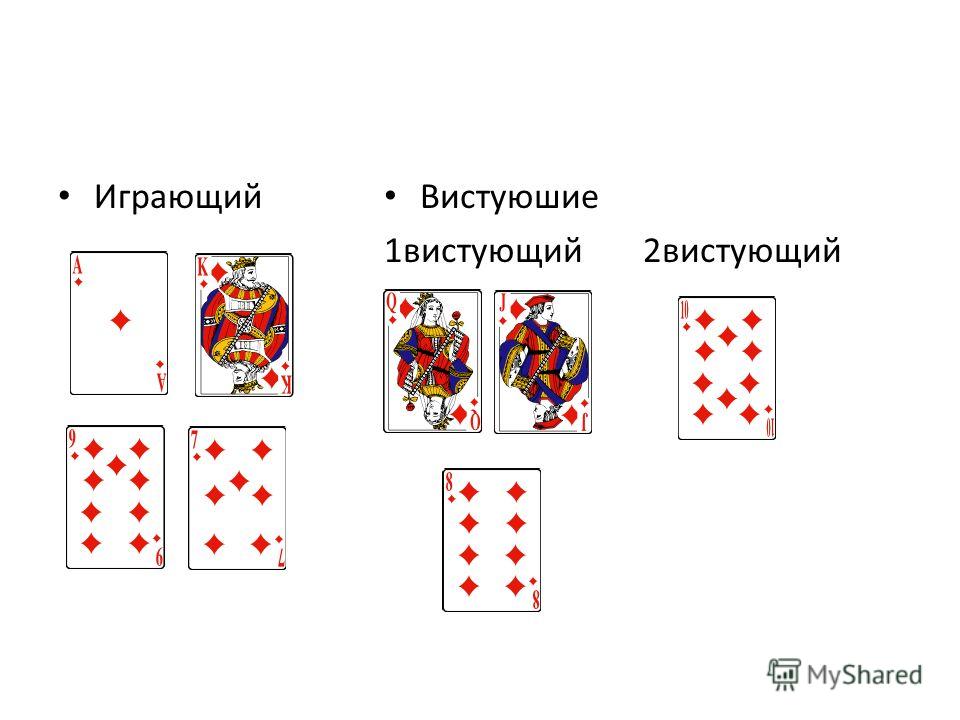
Google ученый
Б. Дебор, Аксиоматическая характеристика функции выбора Борды k , Soc. Выбор благосостояния 9 (1992) 337 — 343.
Google ученый
G.Дебре, Представление упорядочивания предпочтений числовой функцией, в: Decision Processes , eds. R.M. Тралл, Ч. Кумбс и Р.Л. Дэвис, Wiley, New York, 1954, стр. 159–165.
Google ученый
Г. Дебре, Топологические методы в теории кардинальной полезности, в: Математические методы в социальных науках 1959 , ред. К.Дж. Эрроу, С. Карлин и П. Суппес, Stanford University Press, Стэнфорд, Калифорния, 1960, стр.16 –26.
Google ученый
Р. Дешам и Л. Геверс, Лексимин и утилитарные правила: совместная характеристика, J. Econ. Теория 17 (1978) 143 — 163.
Google ученый
Z. Domotor, Упорядоченная сумма и тензорное произведение линейных структур полезности, Теория и решение 11 (1979) 375 — 399.
Domotor, Упорядоченная сумма и тензорное произведение линейных структур полезности, Теория и решение 11 (1979) 375 — 399.
Google ученый
Дж.Дугган, Аксиомы для дизайна комитетов, неопубликованная рукопись, 1993.
Д. Фаркас и С. Ницан, Правило Борда и стабильность Парето: комментарий, Econometrica 47 (1979) 1305–1306.
Google ученый
B. Fine и K. Fine, Социальный выбор и индивидуальный рейтинг, Rev. Econ. Исследования 41 (1974) 303–342, 459 — 475.
Google ученый
П.С. Фишберн, Функции предпочтения, суммирования и социального обеспечения, Менеджмент. 16 (1969) 179 — 186.
Google ученый
P.C. Фишберн, Должен ли социальный выбор быть основан на бинарных сравнениях ?, J. Math. Социология 1 ((1971) 133–142.
Google ученый
P.C. Фишберн, Сравнительный анализ методов групповых решений, Поведение. Sci. 16 (1971) 538 — 544.
Google ученый
П.К. Фишберн, Суммирование функций социального выбора, Econometrica 41 (1973) 1183 — 1196.
Google ученый
P.C. Фишберн, Аксиомы для одобрения голосования: Прямое доказательство, J. Econ. Теория 19 (1978) 180 — 185.
Google ученый
P.C. Фишберн, Симметричное и последовательное агрегирование с дихотомическим голосованием, in: Aggregation and Revelation of Preferences , ed.Ж.-Ж. Лаффонт, Северная Голландия, Амстердам, 1979, стр. 201 — 218.
Google ученый
P.C. Фишберн, Об утилитарной теореме кардинального благосостояния Харшаньи, Теория и решение 17 (1984) 21 — 28.
Google ученый
P.C. Fishburn, Межпрофильные условия и невозможность , Основы чистой и прикладной экономики, Vol. 18, Harwood Academic, Chur, 1987.
Google ученый
P.C. Фишберн и У. Герляйн, правило Борды, позиционное голосование и принцип простого большинства Кондорсе, Public Choice 28 (1976) 79 — 88.
Google ученый
М. Флеминг, Кардинальная концепция благосостояния, Quarterly J. of Economics 66 (1952) 366 — 384.
Google ученый
Дж.М. Флеминг, кардинальное благосостояние и индивидуалистическая этика: комментарий, J. Polit. Экономика 65 (1957) 355–357.
Google ученый
П. Гарденфорс, Функции голосования позиционистов, теория и решение 4 (1973) 1–24.
Google ученый
Л.А. Гудман и Х. Марковиц, Функции социального обеспечения на основе индивидуальных рейтингов, Amer. J. Sociol. 58 (1952) 257 — 262.
Google ученый
Х. Гулликсен, Решение методом наименьших квадратов для парных сравнений с неполными данными, Психометрика 21 (1956) 125 — 134.
Google ученый
Б. Ханссон и Х. Сальквист, Метод доказательства социального выбора с переменным электоратом, J. Econ. Теория 13 (1976) 193–200.
Google ученый
Дж.К. Харшани, Кардинальное благосостояние, индивидуалистическая этика и межличностные сравнения полезности, J. Polit. Экономика 63 (1955) 309 — 321.
Google ученый
Дж. К. Харсани, Нелинейные функции социального обеспечения, теория и решение 6 (1975) 311 — 332.
Google ученый
Дж. К. Харсани, Мораль и теория рационального поведения, в: Утилитаризм и за его пределами , ред.А. Сен и Б. Уильямс, Cambridge University Press, Кембридж, 1982, стр. 39–62.
Google ученый
Д. Генриет, Функция выбора Коупленда: аксиоматическая характеристика, Soc. Выбор благосостояния 2 (1985) 49 — 63.
Google ученый
Л. Кац, Новый индекс статуса, полученный на основе социометрического анализа, Психометрика 18 (1953) 39 — 43.
Google ученый
Р.Л. Кини, Аксиоматизация группового предпочтения с кардинальной полезностью, Управление науки. 23 (1976) 140 — 145.
Google ученый
A.B. Хмельницкая, Проблемы социального выбора с разными шкалами измерения индивидуального благосостояния для разных подгрупп людей, в: Operation Research Proceedings , Springer, Berlin, 1995, pp. 252–257.
252–257.
Google ученый
Дж.-F. Laslier, Турнирные решения и голосование большинством , Springer, Berlin, 1997.
Google ученый
Р.Д. Люс и Х. Райффа, Games and Decisions: Introduction and Critical Review , Wiley, New York, 1957.
Google ученый
Т. Марчант, Агрегирование стоимостных отношений с помощью метода Борда, J. Multi-Crit. Decis. Анальный. 5 (1996) 127 — 132.
Google ученый
Т. Маршан, Кардинальность и оценка Борды, Документ для обсуждения MG 96/9, Université Libre de Bruxelles, 1996.
Дж. Маршак, Рациональное поведение, неопределенные перспективы и измеримые полезности , Econometrica 18 (1950) 111–141.
Google ученый
Э. Маскин, Теорема об утилитаризме, Rev. Econ. Исследования 45 (1978) 93 — 96.
Маскин, Теорема об утилитаризме, Rev. Econ. Исследования 45 (1978) 93 — 96.
Google ученый
В. Мерлин, Некоторые свойства процедур последовательной оценки социального выбора, Препринт, Université de Caen, 1994.
В. Мерлин, Методы подсчета баллов согласованы, Препринт, Université de Caen , 1996.
JW Милнор, Игры против природы, в: Decision Processes , eds. R.M. Тралл, Ч. Кумбс и Р.Л.Дэвис, Wiley, New York, 1954, стр.49 — 60.
Google ученый
П. Монгин, Теорема агрегирования Харшаньи: многопрофильная версия и нерешенные вопросы, Soc. Выбор благосостояния 11 (1994) 331 — 354.
Google ученый
Моркелюас А. Аксиоматическое определение некоторых групповых решений, Литовский математический сборник 11, № 1 (1971) 159–172.
Google ученый
A. Моркелюнас, Два правила социального выбора, подобные правилу множественности и Борда, Математические методы в социальных науках, выпуск 15 (1982) 27 — 36.
Моркелюнас, Два правила социального выбора, подобные правилу множественности и Борда, Математические методы в социальных науках, выпуск 15 (1982) 27 — 36.
Google ученый
Х. Мулен, Аксиомы совместного принятия решений , Cambridge University Press, Кембридж, 1988.
Google ученый
Р.Б. Майерсон, Утилитаризм, эгалитаризм и временной эффект в проблемах социального выбора, Econometrica 49 (1981) 883 — 897.
Google ученый
Майерсон Р. Б., Аксиоматический вывод правил подсчета очков без допущения упорядочения, Soc. Выбор благосостояния 12 (1995) 59 — 74.
Google ученый
С. Ницан и А. Рубинштейн, Дополнительная характеристика метода ранжирования Борда, Public Choice 36 (1981) 153–158.
Google ученый
P. K. Паттанаик, Риск, безличность и функция социального обеспечения, J. Polit. Экономика 76 (1968) 1152 — 1169.
K. Паттанаик, Риск, безличность и функция социального обеспечения, J. Polit. Экономика 76 (1968) 1152 — 1169.
Google ученый
J.T. Richelson, Результат характеризации для правила множественности, J. Econ. Теория 19 (1978) 548–550.
Google ученый
К.W.S. Робертс, Теория межличностной сопоставимости и социального выбора, Rev. Econ. Исследования 47 (1980) 409 — 420.
Google ученый
А. Рубинштейн, Рейтинг участников турнира, SIAM J. Appl. Математика. 38 (1980) 108 — 111.
Google ученый
D.G. Саари, Словарь Борда, Соц. Выбор благосостояния 7 (1990) 279 — 317.
Google ученый
D.Г. Саари, Последовательность процессов принятия решений, Annals Oper. Res. 23 (1990) 107 — 137.
Google ученый
D.G. Саари, Геометрия голосования , Шпрингер, Берлин, 1994.
Google ученый
A.K. Сен, Теория социального выбора: переосмысление, Econometrica 45 (1977) 53–89.
Google ученый
A.К. Сен, О весах и мерах: информационные ограничения в анализе социального обеспечения, Econometrica 45 (1977) 1539 — 1572.
Google ученый
А. Сен и Б. Уильямс (ред.), Утилитаризм и не только , Cambridge University Press, Кембридж, 1982.
Google ученый
J.H. Смит, Корректировка положения в бейсболе с учетом силы играемых команд, American Statistician 10, No.3 (1956) 23 — 24.
Google ученый
J. H. Смит, Агрегация предпочтений с переменным электоратом, Econometrica 41 (1973) 1027–1041.
H. Смит, Агрегация предпочтений с переменным электоратом, Econometrica 41 (1973) 1027–1041.
Google ученый
Дж. Ван Ньюенгизен, Метод Борда, скорее всего, соответствует принципу Кондорсе, Econ. Теория 2 (1992) 69 — 83.
Google ученый
Дж.фон Нейман и О. Моргенштерн, Теория игр и экономического поведения , 2-е изд., Princeton University Press, Princeton, NJ, 1947.
Google ученый
J.A. Веймарк, Пересмотр дискуссии Харсаньи-Сена об утилитаризме, в: Межличностные сравнения благополучия , ред. Дж. Эльстер и Дж. Э. Ремер, Cambridge University Press, Кембридж, 1991, стр. 255 — 320.
Google ученый
Дж.А. Веймарк, Теорема Харшаньи о социальной агрегации и принцип слабого Парето, Soc. Выбор благосостояния 10 (1993) 209 — 221.
Google ученый
E.B. Яновская, Правила социального выбора для разных шкал индивидуальных предпочтений, Труды Всесоюзного института системных исследований, № 6 (1988) 64 — 76.
Google ученый
H.П. Янг, Аксиоматизация правила Борда, J. Econ. Теория 9 (1974) 43 — 52.
Google ученый
л.с. Янг, Функции оценки социального выбора, SIAM J. Appl. Математика. 28 (1975) 824 — 838.
Google ученый
л.с. Янг, Оптимальное ранжирование и выбор из парных сравнений, в: Сбор информации и принятие решений группой , ред. Б. Грофман, Г.Оуэн, JAI Press, Гринвич, Коннектикут, 1986, стр. 113–122.
Google ученый
л.с. Янг и А. Левенглик, Последовательное расширение избирательного принципа Кондорсе, SIAM J. Appl. Математика. 35 (1978) 285–300.
Appl. Математика. 35 (1978) 285–300.
Google ученый
Э. Цермело, Die Berechnung der Turnier-Ergebnisse als ein Maximumproblem der Wahrscheinlichkeitsrechnung, Math. Zeit. 29 (1928) 436 — 460.
Google ученый
Оценка сводной оценки на основе предпочтений для информационной системы измерения исходов, сообщаемых пациентами: Система оценки PROMIS ®-Preference (PROPr)
Фон: Показатели качества жизни, связанные со здоровьем (HRQL), основанные на предпочтениях, используются для оценки здоровья населения и пациентов, а также для анализа экономической эффективности.Информационная система оценки исходов, сообщаемых пациентами Национального института здравоохранения (PROMIS ® ), состоит из показателей исходов, сообщаемых пациентами, разработанных с использованием теории ответа на вопросы. PROMIS нуждается в прямой системе оценки на основе предпочтений для присвоения значений состояниям здоровья.
PROMIS нуждается в прямой системе оценки на основе предпочтений для присвоения значений состояниям здоровья.
Задача: Для получения оценок на основе социальных предпочтений по 7 доменам PROMIS: когнитивные функциональные способности, депрессия, усталость, болевые ощущения, физические функции, нарушения сна и способность участвовать в социальных ролях и действиях.
Параметр: Онлайн-опрос репрезентативной выборки в США (n = 983).
Методы: Предпочтения для состояний работоспособности PROMIS были получены с помощью стандартной азартной игры, чтобы получить как функции оценки с одним атрибутом для каждого из 7 доменов PROMIS, так и функцию мультипликативной мультиатрибутной полезности (оценки).
Полученные результаты: 7 функций оценки с одним атрибутом были подобраны с использованием изотонической регрессии с линейной интерполяцией. Функция мультипликативной сводки множественных атрибутов оценивает полезности для состояний множественной работоспособности PROMIS по шкале, где 0 — полезность отсутствия, а 1 — полезность «полного здоровья». Наименьшая возможная оценка — -0,022 (для состояния хуже мертвого), а наивысшая возможная оценка — 1.
Ограничения: Из онлайн-опроса систематически исключаются некоторые подгруппы, например, слабовидящие и неграмотные.
Выводы: Общая система оценки, основанная на социальных предпочтениях, теперь доступна для всех исследований, в которых используются эти 7 областей здоровья PROMIS.
Ключевые слова: ПРОМИС; Население США в целом; полезность для здоровья; качество жизни, связанное со здоровьем.
Поперечная валидация балльной системы PROMIS-Preference
Абстрактные
Цели
Оценка PROMIS-Preference (PROPr) — это недавно разработанная сводная оценка для Информационной системы оценки исходов, сообщаемых пациентами (PROMIS).PROPr — это система оценки на основе предпочтений для семи доменов PROMIS, созданная с использованием теории мультипликативной мультиатрибутной полезности. Он служит общей, основанной на социальных предпочтениях системой итоговых оценок качества жизни, связанного со здоровьем. Эта рукопись оценивает конструктивную валидность PROPr в двух больших выборках из общей популяции США.
Методы
Мы использовали 2 онлайн-панельных опроса, опрос PROPr Estimation Survey и опрос Profiles-Health Utilities Index (HUI). Оба включали показатель PROPr, демографическую информацию о пациентах, хронические состояния, о которых сообщают пациенты, и другие сводные баллы на основе предпочтений: EuroQol-5D (EQ-5D-5L) и HUI в оценочном опросе PROPr и HUI в Profiles-HUI. Опрос. HUI был оценен как Mark 2, так и Mark 3. Достоверность известных групп оценивалась с использованием стратифицированных по возрасту и полу средних баллов и оценок воздействия на состояние здоровья. Оценки воздействия на состояние были созданы с использованием обычной регрессии наименьших квадратов, в которой сводный балл регрессировал по возрасту, полу и одному состоянию здоровья.Коэффициент состояния здоровья — это оценочный эффект на оценку предпочтения наличия состояния по сравнению с отсутствием его. Конвергентная достоверность оценивалась с использованием корреляций Пирсона между PROPr и другими итоговыми баллами.
Оба включали показатель PROPr, демографическую информацию о пациентах, хронические состояния, о которых сообщают пациенты, и другие сводные баллы на основе предпочтений: EuroQol-5D (EQ-5D-5L) и HUI в оценочном опросе PROPr и HUI в Profiles-HUI. Опрос. HUI был оценен как Mark 2, так и Mark 3. Достоверность известных групп оценивалась с использованием стратифицированных по возрасту и полу средних баллов и оценок воздействия на состояние здоровья. Оценки воздействия на состояние были созданы с использованием обычной регрессии наименьших квадратов, в которой сводный балл регрессировал по возрасту, полу и одному состоянию здоровья.Коэффициент состояния здоровья — это оценочный эффект на оценку предпочтения наличия состояния по сравнению с отсутствием его. Конвергентная достоверность оценивалась с использованием корреляций Пирсона между PROPr и другими итоговыми баллами.
Результаты
Выборка состояла из 983 респондентов из оценочного опроса PROPr и 3000 респондентов из опроса Profiles-HUI.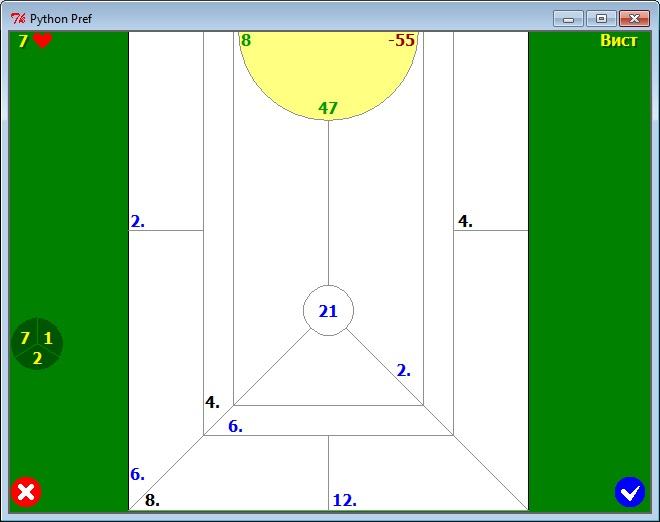 Стратифицированные по возрасту и полу средние баллы PROPr были ниже, чем баллы EQ-5D и HUI, при этом меньшее количество субъектов имели баллы, соответствующие идеальному здоровью по PROPr.В обзоре PROPr Estimation все 11 оценок воздействия условий были статистически значимыми с использованием PROPr, 8 были статистически значимыми по EQ-5D, 7 были статистически значимыми по HUI Mark 2 и 9 были статистически значимыми по HUI Mark 3. В профилях: В исследовании HUI все 21 оценка воздействия на состояние были статистически значимыми с использованием сводных баллов всех трех систем оценки. В этих выборках корреляция между PROPr и другими суммарными показателями варьировалась от 0,67 до 0.70.
Стратифицированные по возрасту и полу средние баллы PROPr были ниже, чем баллы EQ-5D и HUI, при этом меньшее количество субъектов имели баллы, соответствующие идеальному здоровью по PROPr.В обзоре PROPr Estimation все 11 оценок воздействия условий были статистически значимыми с использованием PROPr, 8 были статистически значимыми по EQ-5D, 7 были статистически значимыми по HUI Mark 2 и 9 были статистически значимыми по HUI Mark 3. В профилях: В исследовании HUI все 21 оценка воздействия на состояние были статистически значимыми с использованием сводных баллов всех трех систем оценки. В этих выборках корреляция между PROPr и другими суммарными показателями варьировалась от 0,67 до 0.70.
Выводы
Эти результаты подтверждают конструктивную валидность PROPr с использованием выборок из общей популяции США.
Образец цитирования: Hanmer J, Dewitt B, Yu L, Tsevat J, Roberts M, Revicki D, et al. (2018) Поперечная валидация балльной системы PROMIS-Preference. PLoS ONE 13 (7): e0201093. https://doi.org/10.1371/journal.pone.0201093
Редактор: Нан Луо, Национальный университет Сингапура, СИНГАПУР
Поступила: 21 марта 2018 г .; Одобрена: 9 июля 2018 г .; Опубликован: 31 июля 2018 г.
Авторские права: © 2018 Hanmer et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Все файлы данных доступны в Open Science Framework (https://osf.io/t896p/) и (Dataverse: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi : 10.7910 / DVN / P7UKWR).
Финансирование: Джанель Ханмер получила поддержку Национальных институтов здравоохранения в рамках гранта номер KL2 TR001856.Сбор данных был поддержан Национальными институтами здравоохранения в рамках гранта номер UL1TR000005. Барри Девитт получил частичную поддержку со стороны Совета по социальным и гуманитарным исследованиям Канады. Дэвид Селла, Рон Д. Хейс, Пол А. Пилконис и Деннис А. Ревицки были поддержаны грантом Национального института рака № 1U2C-CA186878-01 и дополнением к гранту статистического центра PROMIS № 3U54AR057951-04S4. Барух Фишхофф был частично поддержан Шведским фондом гуманитарных и социальных наук.Соглашения о финансировании гарантировали авторам независимость в разработке исследования, интерпретации данных, написании и публикации отчета. Evidera, Inc оказала поддержку в виде зарплаты Деннису Ревицки, но не играла никакой дополнительной роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи. Конкретные роли этих авторов сформулированы в разделе «Авторский вклад».
Конкурирующие интересы: Дэвид Фини имеет долю в компании Health Utilities Incorporated, Дандас, Онтарио, Канада.HUInc. распространяет материалы Health Utilities Index (HUI), защищенные авторским правом, и дает методические рекомендации по использованию HUI. Деннис Ревицки работает в Evidera, Inc. Это не влияет на нашу приверженность политике PLOS ONE в отношении обмена данными и материалами.
Введение
Отчеты пациентов о функционировании и благополучии или связанном со здоровьем качестве жизни (HRQoL) являются важными результатами здравоохранения и политики [1,2]. Измерения HRQoL могут быть ориентированы на заболевание, обеспечивая подробное измерение симптомов, эффектов лечения и побочных эффектов, относящихся к конкретному состоянию.Меры также могут быть общими, обеспечивая общее описание здоровья, не ограничиваясь одной системой органов или заболеванием [3]. Однако распространение показателей HRQoL затруднило сравнение результатов исследований, в которых используются разные показатели [4,5].
HRQoL можно дополнительно разделить на категории с использованием показателей профиля здоровья или показателей на основе предпочтений. Профильные показатели обеспечивают описание множества областей здоровья, таких как физическое функционирование, психическое здоровье и боль. Эти меры дают несколько баллов — по одной для каждой области здоровья.Меры на основе предпочтений также охватывают несколько областей здоровья, но объединены в единую сводную оценку на основе предпочтений по шкале, где 0 — «мертвый», а 1 — «полное состояние»). Шкала на основе предпочтений позволяет оценить количество лет жизни с поправкой на качество (QALY), что позволяет сравнивать варианты лечения при принятии клинических решений и в экономическом анализе [2, 6–8].
Наиболее широко используемые общие меры, основанные на предпочтениях, включают EuroQol-5D (EQ-5D) [9], индекс медицинских услуг (HUI) [10–11], SF-6D [12] и качество благополучия. Индекс [13].Однако у каждого из них есть некоторые ограничения: (1) большая доля респондентов, получивших оценку на самом верху или на самом низу шкалы (т. Е. Потолочные эффекты для очень здоровых или минимальные эффекты для очень больных), (2) неточные измерения для отдельных лиц: (3) плохо сформулированные вопросы, например, те, которые объединяют концепции (двузначные вопросы), и (4) недостаточный охват всего диапазона здоровья [14]. Эти ограничения возникают из-за описания здоровья, используемого в этих измерениях, а не из-за метода подсчета баллов.
Недавние усилия по разработке следующего поколения показателей профиля здоровья с использованием Теории ответа на вопросы (IRT) [15] создали возможность использовать эти улучшения в показателях, основанных на предпочтениях [14]. В частности, IRT использовалась для разработки Информационной системы измерения исходов, сообщаемых пациентами (PROMIS) при поддержке Национальных институтов здравоохранения [16,17]. PROMIS устраняет несколько ограничений существующих общих критериев предпочтений, включая: (1) охват более широкого диапазона каждой области здоровья, (2) измерение индивидуального состояния здоровья с большей точностью и (3) использование тщательно разработанных и проверенных вопросов.Система оценки на основе предпочтений для PROMIS создаст возможность одновременного сбора оценок как профиля здоровья, так и оценок на основе предпочтений.
Используя информацию от экспертов по измерениям и членов сообщества, мы разработали систему оценки предпочтений, основанную на 7 областях измерения PROMIS, известную как PROMIS-Preference (PROPr) [18, 19]. Алгоритм оценки был оценен с использованием большой репрезентативной выборки неинституционализированного населения США [20]. PROPr — это первая сводная оценка на основе предпочтений, которая напрямую связывает функции на основе предпочтений с доменами здоровья, измеренными IRT.Таким образом, PROPr получает многие преимущества описательной системы на основе IRT, включая гибкое администрирование элементов из доменов работоспособности, используемых для создания PROPr.
Прежде чем какая-либо мера может быть принята для широкого использования, необходимо продемонстрировать ее обоснованность [3]. Мы использовали 2 поперечных опроса населения США в целом, чтобы оценить конструктную валидность PROPr.
Методы
Источники данных
Первым набором данных был опрос PROPr Estimation Survey, собранный в Интернете ICF и SurveyNow, которые поддерживают группу предварительно проверенных лиц, в первую очередь для исследования рынка.Данные были собраны весной 2016 года. Выборка обследования должна была быть репрезентативной для населения США по возрасту, полу, расе, этнической принадлежности, образованию и доходу в соответствии с переписью 2010 года. В качестве компенсации за заполнение опроса участники могли выбрать одно из нескольких вознаграждений, включая подарочные карты и баллы программы вознаграждений. Исследование было одобрено институциональным наблюдательным советом ICF International (исследование № FWA00002349). Ответы были деидентифицированы до того, как их получили авторы.Полное описание исследования доступно в техническом отчете PROPr [21]. Данные, использованные в этом анализе, доступны в Интернете на сайте Open Science Framework [22].
Вторым набором данных был опрос Profiles-HUI, собранный онлайн с помощью интернет-панели Op4G. Op4G поддерживает национальную выборку США, и участники должны регулярно обновлять демографическую информацию. Выборка была определена с использованием квот по региону, расе / этнической принадлежности, образованию и половозрастным слоям в соответствии с переписью 2010 года.Участники исследования получили номинальные стимулы от Op4G за прохождение опроса. Конкретный характер и стоимость поощрения варьировались, но не превышали 10 долларов США. Опрос был одобрен институциональным наблюдательным советом Северо-Западного университета (исследование № STU00016635). Данные, использованные в этих анализах, доступны на сайте Dataverse [23].
В данном исследовании использовались обезличенные данные, предоставленные исследовательскими компаниями. Каждое исследование анализировалось отдельно. Участники оценочного опроса PROPr были рандомизированы для получения в первую очередь анкеты EQ-5D-5L, HUI, состояния здоровья или PROMIS Global.Затем все участники получили краткую форму PROMIS-29 и PROMIS Cognitive Function (которая предоставила данные по 7 доменам, необходимым для PROPr) и выполнили оценочные упражнения PROPr. После оценочных упражнений участник заполнил остальные разделы (EQ-5D-5L, HUI, состояние здоровья и опросник PROMIS Global) в случайном порядке. Все участники опроса Profiles-HUI заполнили одну и ту же форму опроса. Сначала они заполнили набор социально-демографических и сопутствующих заболеваний, затем форму PROMIS Global, набор вопросов PROMIS из различных банков, а затем HUI.Оба опроса запрашивали у респондентов демографическую информацию, включая их возраст и пол, а также об их состоянии здоровья, используя стандартные формулировки национального опроса о состоянии здоровья (например, «Говорили ли вам когда-либо врач или другой медицинский работник, что у вас ишемическая болезнь сердца? ? ») [24]. Оценочный опрос PROPr включал 11 состояний здоровья, а опрос Profiles-HUI — 21 состояние здоровья.
Меры
PROPr.
PROPr основан на уровнях функционирования для 7 доменов PROMIS: когнитивные функции, депрессия, усталость, болевые ощущения, физические функции, нарушения сна и способность участвовать в социальных ролях и действиях.Вопросы PROMIS относятся к собственному здоровью респондента «за последние 7 дней» и имеют 5 вариантов ответа. В опросе PROPr Estimation использовались стандартизированные краткие формы из 4 пунктов для каждой из этих областей. Опрос Profiles-HUI собрал от 8 до 13 элементов на домен. Домены оценивались службой скоринга в Assessment Center с включением параметров IRT по умолчанию для каждого элемента [25]. Алгоритм подсчета очков PROPr был разработан на основе стандартных оценок азартных игр по выборке из США [20]. Возможные значения PROPr варьируются от -0.022 до 1.0.
EQ-5D-5L.
Модель EQ-5D-5L была собрана в рамках оценочного обзора PROPr. Вопросы EQ-5D-5L относятся к «вашему здоровью сегодня». Описательная система EQ-5D имеет 5 областей (мобильность, уход за собой, обычная деятельность, боль / дискомфорт и тревога / депрессия). В оценочном обзоре PROPr использовалась версия EQ-5D-5L, каждая с 5 вариантами ответа [9, 26]. Для этого исследования мы применили функцию переходного канала EQ-5D-3L к набору значений компромиссного времени в США [27]. Возможные оценки варьируются от -0.109 к 1.0.
Индекс медицинских услуг (HUI).
Самостоятельно заполняемый опросник HUI, позволяющий оценивать как Mark 2, так и Mark 3, был включен в оба опроса [10,11]. Вопросы HUI относятся к «вашему уровню способностей или инвалидности за последнюю неделю». HUI Mark 2 определяет состояние здоровья по 6 атрибутам (ощущения, подвижность, эмоции, познание, уход за собой и боль). HUI Mark 3 определяет здоровье по 8 характеристикам (зрение, слух, речь, передвижение, ловкость, эмоции, познание и боль).Алгоритмы подсчета баллов для HUI Mark 2 и HUI Mark 3 были получены на основе стандартных оценок азартных игр, сделанных взрослыми в выборках сообществ в Гамильтоне, Онтарио, и используют мультипликативные функции полезности с несколькими атрибутами. Оценка HUI Mark 2 варьируется от -0,03 до 1,0; Оценка HUI Mark 3 варьируется от -0,36 до 1,0.
Статистический анализ
Каждый опрос анализировался отдельно. Мы рассчитали процентные значения для категориальных переменных демографии и состояния здоровья. Мы также создали гистограммы итоговых баллов для каждой выборки.Конвергентная достоверность оценивалась с использованием корреляций Пирсона между итоговыми баллами внутри субъектов (то есть путем сравнения баллов PROPr, HUI и EQ-5D для каждого участника в каждом из двух наборов данных).
Достоверность известных групп оценивалась с использованием стратифицированных по возрасту и полу средних баллов для всех суммарных баллов. Мы ожидали, что PROPr покажет те же закономерности в средних баллах, стратифицированных по возрасту и полу, что и другие сводные баллы. Достоверность известных групп также оценивалась с использованием оценок воздействия на состояние здоровья, которые были созданы с использованием обычной регрессии наименьших квадратов, в которой сводный балл регрессировал по возрасту, полу и одному состоянию здоровья.Коэффициент состояния здоровья — это оценочный эффект на оценку предпочтения наличия состояния по сравнению с отсутствием его. Для каждого условия был проведен отдельный анализ.
Все анализы были выполнены с использованием SAS 9.4 (Институт SAS, Кэри, Северная Каролина).
Результаты
В таблице 1 приведены демографические характеристики каждой выборки. В выборке опроса PROPr Estimation было 983 респондента, а в выборке опроса Profiles-HUI — 3000 респондентов. Для сравнения мы отображаем информацию о возрасте, поле и расе / этнической принадлежности из переписи населения США 2010 года [28], а также информацию о распространенности хронических заболеваний, о которой сообщают сами люди, из Национального опроса по вопросам здоровья в 2016 году [29].
На рис. 1 и 2 показано распределение итоговых оценок в выборках PROPr Estimation и Profiles-HUI, соответственно. EQ-5D, HUI Mark 2 и HUI Mark 3 в этих образцах имеют эффект потолка. Процент респондентов в опросе PROPr Estimation с максимальной оценкой составил 28% для EQ-5D, 11% для HUI Mark 2, 10% для HUI Mark 3 и 2% для PROPr. Процент респондентов в опросе Profiles-HUI с максимальным баллом составил 9% для HUI Mark 2, 8% для HUI Mark 3 и 0.4% на ПРОП.
Рис. 1. Распределение итоговых баллов в выборке PROPr Estimation.
HUI 2 — это индекс Health Utilities Mark 2, HUI 3 — это Health Utilities Index Mark 3, EQ-5D US Mapped — это Euroqol-5D-5L, сопоставленный с оценочным набором США, PROPr — это оценка PROMIS-Preference.
https://doi.org/10.1371/journal.pone.0201093.g001
В таблицах 2 и 3 приведены корреляции Пирсона между итоговыми баллами. В этих выборках корреляция между PROPr и другими суммарными показателями варьировалась от 0.66 до 0,70. Корреляция между HUI Mark 2 и HUI Mark 3 завышена, потому что для создания обеих оценок использовались одни и те же вопросы.
PROPr, который не имеет эффекта потолка в этих выборках, имеет самые низкие средние баллы с разбивкой по возрасту и полу. На рисунках 3 и 4 показаны средние значения с поправкой на возраст и пол в выборках PROPr Estimation и Profiles-HUI, соответственно. В национальных репрезентативных выборках показатели полезности для здоровья обычно ниже у женщин, чем у мужчин, и снижаются с возрастом [30–32].В выборке для оценки PROPr у мужчин более низкие оценки, чем у женщин в более молодых возрастных группах, тогда как у женщин более низкие оценки в старших возрастных группах. Связь между возрастной группой и средним баллом в этой выборке не является монотонной, хотя все сводные баллы обычно меняются в одном и том же направлении между группами; например, все суммарные баллы для мужчин в возрасте 45–54 лет ниже, чем для мужчин в возрасте 55–64 лет.
Рис. 3. Стратифицированные по возрасту и полу средние баллы в выборке для оценки PROPr.
HUI 2 — это индекс Health Utilities Mark 2, HUI 3 — это Health Utilities Index Mark 3, EQ-5D US Mapped — это Euroqol-5D-5L, сопоставленный с оценочным набором США, PROPr — это оценка PROMIS-Preference.
https://doi.org/10.1371/journal.pone.0201093.g003
Рис. 4. Стратифицированные по возрасту и полу средние баллы в выборке Profiles-HUI.
HUI 2 — это оценка 2 индекса медицинских услуг, HUI 3 — оценка 3 индекса коммунальных услуг, PROPr — оценка PROMIS-Preference.
https://doi.org/10.1371/journal.pone.0201093.g004
На рисунках 5 и 6 показано влияние состояния здоровья с поправкой на возраст и пол в выборках PROPr Estimation и Profiles-HUI, соответственно.В обзоре PROPr Estimation все 11 оценок воздействия условий статистически значимо отличались от нуля (p <0,05) с использованием PROPr, 8 были статистически значимыми по EQ-5D, 7 были статистически значимыми по HUI Mark 2 и 9 были статистически значимыми по Оценка HUI 3. В обзоре Profiles-HUI все 21 оценка воздействия на состояние были статистически значимыми с нуля (p <0,05) для всех итоговых баллов всех трех систем оценки.
Рис. 5. Влияние состояния здоровья с разбивкой по возрасту и полу в выборке для оценки PROPr.
HUI 2 — это индекс Health Utilities Mark 2, HUI 3 — это Health Utilities Index Mark 3, EQ-5D US Mapped — это Euroqol-5D-5L, сопоставленный с оценочным набором США, PROPr — это оценка PROMIS-Preference. Статистически значимые оценки отмечены звездочкой.
https://doi.org/10.1371/journal.pone.0201093.g005
Рис. 6. Влияние стратифицированного по возрасту и полу состояния здоровья в выборке Profiles-HUI.
HUI 2 — это оценка 2 индекса медицинских услуг, HUI 3 — оценка 3 индекса коммунальных услуг, PROPr — оценка PROMIS-Preference.Все оценки статистически значимы.
https://doi.org/10.1371/journal.pone.0201093.g006
Среднее воздействие на состояние, измеренное с помощью PROPr, наиболее похоже на HUI Mark 3 в опросе PROPr Estimation (среднее значение -0,136 для PROPr, -0,138 для HUI Mark 3, -0,095 для HUI Mark 2 и -0,061 для EQ-5D), тогда как он больше всего похож на HUI Mark 2 в обзоре Profiles-HUI (среднее значение -0,137 для PROPr, -0,173 для HUI Mark 2 и -0,268 для HUI Mark 3).HUI Mark 3 обычно имеет наибольшие оценки воздействия в обоих исследованиях. Стандартная ошибка этих коэффициентов была наименьшей для PROPr как в оценочном опросе PROPr (среднее значение составляет 0,036 для PROPr, 0,077 для HUI Mark 3, 0,051 для HUI Mark 2 и 0,041 для EQ-5D), так и в опросе Profiles-HUI (среднее значение составляет 0,021 для PROPr, 0,045 для HUI Mark 2 и 0,069 для HUI Mark 3). Корреляция условий по оценке воздействия аналогична для всех итоговых баллов с корреляцией Пирсона более 0,70 для всех сравнений и корреляцией Спирмена более 0.68 для всех сравнений.
Обсуждение
В этом отчете представлена первая оценка валидности балла PROPr с использованием 2 больших наборов перекрестных данных по населению США в целом. Мы обнаружили, что PROPr имеет хорошую конвергентную валидность с двумя другими сводными показателями здоровья на основе предпочтений — EQ-5D и HUI. Мы также обнаружили, что PROPr различает людей с различными хроническими заболеваниями и без них. Относительное влияние этих хронических состояний, измеренное с помощью PROPr, было аналогично другим сводным баллам, основанным на предпочтениях.Взятые вместе, эти результаты дают веское обоснование использования PROPr для количественной оценки связанного со здоровьем качества жизни для различных целей, включая расчет агрегированных индексов заболеваемости и смертности, таких как QALY.
В этих выборках корреляция между PROPr и другими суммарными показателями варьировалась от 0,66 до 0,70. Предыдущее исследование, в котором совместно применялись сводные измерения на основе предпочтений в большой общей популяции США, обнаружило корреляцию от 0,60 до 0,71 [31, 33]. Максимальная корреляция между двумя показателями — это квадратный корень из произведения их надежности; поскольку надежность большинства мер по обеспечению здоровья ниже 0.75 максимальная корреляция будет ниже 0,75. Обратите внимание, что корреляция между HUI Mark 2 и HUI Mark 3 завышена, потому что для создания обеих оценок использовались одни и те же вопросы. Также важно отметить, что перекрестные корреляции не обязательно предсказывают корреляции в показателях продольных изменений [34, 35].
Хотя оценки PROPr хорошо коррелируют с оценками EQ-5D и HUI, оценки PROPr обычно ниже, чем соответствующие оценки EQ-5D, HUI2 и HUI3. Мы ожидали, что баллы PROPr будут ниже, чем эти унаследованные меры, потому что наилучшее возможное состояние здоровья, описанное в PROPr, качественно намного лучше, чем лучшее состояние здоровья, описанное в унаследованных показателях.Например, наивысший физический уровень в PROPr — это «способность одеваться, включая завязывание шнурков и застегивание одежды без каких-либо проблем. и могут без труда бегать 100 ярдов (100 м)». Напротив, наивысший физический уровень функционирования в EQ-5D — «У меня нет проблем с ходьбой», а в HUI Mark 3 «Я полностью использую 2 руки и 10 пальцев» и Я могу ходить вокруг соседство без затруднений и без прогулочного инвентаря.«Увеличение эффективного диапазона измерения PROPr« поднимает планку »и позволяет достичь 1,0 балла для наилучшего состояния здоровья. В результате эффекты потолка в общей популяции менее распространены, а средние и медианные баллы значительно ниже с PROPr по сравнению с традиционными показателями. Другое объяснение этого вывода заключается в том, что баллы PROPr, проанализированные в этом отчете, были собраны с использованием как минимум 32 вопросов, что дает респондентам больше возможностей сообщить о не лучшем состоянии здоровья по сравнению с другими анкетами (например.g., есть только 5 вопросов для EQ-5D).
Система подсчета баллов PROPr была построена с использованием вклада экспертов в области измерения профиля здоровья и предпочтений на основе IRT, а также рекомендаций членов сообщества. Окончательный алгоритм подсчета баллов оценивался с использованием теории полезности с множеством атрибутов и был основан на данных о предпочтениях из большой репрезентативной выборки неинституционализированного населения США. PROPr — это первая оценка, которая связывает служебные функции с одним атрибутом с доменами работоспособности, измеряемыми IRT.Таким образом, PROPr получает преимущества описательной системы на основе IRT, включая гибкое администрирование элементов из 7 банков элементов, используемых для построения PROPr, и более тонкую детализацию его шкалы полезности, чем у других систем оценки.
Паттерны стратифицированных по возрасту и полу средних в сводных оценках на основе предпочтений для этих выборок не соответствовали паттернам, наблюдаемым в обследованиях с репрезентативной выборкой, таких как Панельное обследование медицинских расходов [31, 36]. В частности, у мужчин были более низкие средние баллы, чем у женщин в нескольких возрастных группах, и связь между возрастной группой и средним баллом не была монотонной.Эти различия предполагают, что образцы, использованные в этом отчете, хотя и взяты из общего населения США, не являются репрезентативными для населения США в целом. Таким образом, представленные средние значения не следует использовать в качестве национальных нормативных значений [37]. Точно так же оценки воздействия на состояние здоровья не могут быть полностью применимы к другим исследованиям.
Несмотря на то, что все оценки, используемые в этом исследовании, имеют разные возможные диапазоны оценок, все они привязаны к «мертвому», привязанному к 0, и «полному здоровью», привязанному к 1.0 и, как правило, не масштабируются для использования в анализе полезности затрат. PROPr имел более низкие средние баллы, чем EQ-5D-5, HUI2 или HUI3, но влияние состояния, измеренное PROPr, имело такую же величину, как HUI3 в опросе PROPr Estimation и HUI2 в опросе Profiles-HUI. То, что разные показатели полезности для здоровья дают разные оценки как поперечных различий между группами, так и продольных изменений внутри групп, наблюдалось в нескольких других исследованиях [31, 34, 35]. Несмотря на то, что в ходе опросов были собраны одни и те же данные о состоянии болезни, сравнение воздействия болезни ограничено, поскольку серьезность заболевания не измерялась, и могут быть различия в степени тяжести заболевания или статусе симптомов.Предполагаемое влияние хронических состояний было как в ожидаемом направлении (группа с заболеванием имеет более низкое среднее значение, чем в группе без этого состояния), так и статистически значимым. В будущем потребуется работа по установлению пороговых значений для клинически значимой разницы в оценках PROPr, поскольку они также различаются между оценками, основанными на предпочтениях.
Заключение
Результаты, представленные в этом отчете, подтверждают конструктную валидность для PROPr — она коррелирует с другими широко используемыми обобщенными сводными оценками, основанными на предпочтениях, и у пациентов с хроническим заболеванием баллы ниже, чем у тех, у кого нет болезни.Дальнейшая работа необходима для сбора баллов PROPr из репрезентативной на национальном уровне выборки, создания переходов к устаревшим измерениям и проверки PROPr с использованием лонгитюдного сбора данных.
Благодарности
Мы хотели бы выразить нашу благодарность участникам этих опросов, без которых эта работа была бы невозможна. Мы также признательны за конструктивные комментарии двух рецензентов.
Список литературы
- 1. МакХорни, Калифорния. Методы оценки состояния здоровья взрослых: прошлые достижения и будущие вызовы.Ежегодный обзор общественного здравоохранения. 1999 Май; 20 (1): 309–35.
- 2. Уилсон И.Б., Клири П.Д. Связь клинических переменных с качеством жизни, связанным со здоровьем: концептуальная модель результатов для пациентов. Джама. 1995, 4 января, 273 (1): 59–65. pmid: 7996652
- 3. Макдауэлл I. Измерение здоровья: руководство по оценочным шкалам и анкетам. Издательство Оксфордского университета; 2006 9 марта.
- 4. Тенгс Т.О., Уоллес А. Тысяча оценок качества жизни, связанных со здоровьем. Медицинская помощь.2000 июн 1: 583–637.
- 5. Ханмер Дж., Черепанов Д., Палта М., Каплан Р. М., Фини Д., Фрайбек Д. Г.. Воздействие на состояние здоровья в репрезентативном на национальном уровне перекрестном обследовании существенно различается в зависимости от индекса здоровья, основанного на предпочтениях. Принятие медицинских решений. 2016 Февраль; 36 (2): 264–74. pmid: 26314728
- 6. Торранс GW. Измерение состояния здоровья коммунальных услуг для экономической оценки: обзор. Журнал экономики здравоохранения. 1 марта 1986 г.; 5 (1): 1–30. pmid: 10311607
- 7.Драммонд М.Ф., Скульпер М.Дж., Клэкстон К., Стоддарт Г.Л., Торранс Г.В. Методы экономической оценки программ здравоохранения. Издательство Оксфордского университета; 2015 24 сентября.
- 8. Neumann PJ, Sanders GD, Russell LB, Siegel JE, Ganiats TG, редакторы. Экономическая эффективность в здравоохранении и медицине. Издательство Оксфордского университета; 2017 3 октября
- 9. Брукс Р., Рабин Р., Де Чарро Ф., редакторы. Измерение и оценка состояния здоровья с помощью EQ-5D: европейская перспектива: данные исследовательской программы EuroQol BIOMED.Springer Science & Business Media; 2013 9 марта
- 10. Фини Д., Ферлонг В., Торранс Г. В., Голдсмит С.Х., Чжу З., ДеПау С. и др. Служебные функции с несколькими атрибутами и одним атрибутом для системы с индексом 3 для служебных программ. Медицинская помощь. 2002, 1 февраля; 40 (2): 113–28. pmid: 11802084
- 11. Фини Д., Торранс Г., Ферлонг В. Индекс коммунальных услуг. Глава 26 В Берте Спилкере, изд. Качество жизни и фармакоэкономика в клинических исследованиях. Второе издание. Филадельфия: Lippincott-Raven Press, 1996, стр. 239–252.
- 12. Brazier JE, Roberts J. Оценка состояния здоровья на основе предпочтений из SF-12. Медицинская помощь. 2004, 1 сентября; 42 (9): 851–9. pmid: 15319610
- 13. Каплан RM, Андерсон JP. Общая модель политики работоспособности: обновления и приложения. Исследования служб здравоохранения. 1988 июн; 23 (2): 203. pmid: 3384669
- 14. Ханмер Дж., Фини Д., Фишхофф Б., Хейс Р. Д., Хесс Р., Пилконис П. А. и др. ОБЕЩАНИЕ QALYs. Здоровье и качество жизни.2015 11 августа; 13 (1): 122.
- 15. Embretson SE, Reise SP. Теория отклика предмета. Психология прессы; 2013 5 сентября
- 16. Селла Д., Яунт С., Ротрок Н., Гершон Р., Кук К., Рив Б. и др. Информационная система измерения результатов, сообщаемых пациентами (PROMIS): прогресс группы сотрудничества NIH Roadmap в течение первых двух лет. Медицинская помощь. 2007 Май; 45 (5 Приложение 1): S3.
- 17. Селла Д., Райли В., Стоун А., Ротрок Н., Рив Б., Йонт С. и др.Информационная система для измерения результатов, сообщаемых пациентами (PROMIS), разработала и протестировала свою первую волну банков показателей состояния здоровья взрослых, сообщаемых самими пациентами: 2005–2008 гг. Журнал клинической эпидемиологии. 30 ноября 2010 г.; 63 (11): 1179–94. pmid: 20685078
- 18. Ханмер Дж., Селла Д., Фини Д., Фишхофф Б., Хейс Р. Д., Хесс Р. и др. Выбор ключевых областей здоровья из PROMIS для общей системы оценки на основе предпочтений. Исследование качества жизни. 2017 г. 1 декабря; 26 (12): 3377–85. pmid: 28825177
- 19.Ханмер Дж., Селла Д., Фини Д., Фишхофф Б., Хейс Р. Д., Хесс Р. и др. Оценка вариантов представления состояний работоспособности из банков позиций PROMIS для оценки. Исследование качества жизни. 2018 апр 12: 1–9. [epub перед печатью]
- 20. Девитт Б., Селла Д., Фини Д., Фишхофф Б., Хейс Р.Д., Хесс Р. и др. Оценка сводной оценки на основе предпочтений для информационной системы измерения исходов, сообщаемых пациентами: система оценки PROMIS-Preference (PROPr). Принятие медицинских решений.2018 26 июня: 1–9 [epub перед печатью]
- 21. Доступно по адресу: http://janelhanmer.pitt.edu/ProPr.html Цитировано 21 марта 2018 г.
- 22. Доступно по ссылке: https://osf.io/t896p/ Цитировано 21 марта 2018 г.
- 23. Доступно по адресу: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/P7UKWR Цитировано 21 марта 2018 г.
- 24. Доступно по адресу: https://www.cdc.gov/nchs/nhis/nhis_questionnaires.htm Цитата: 21 марта 2018 г.
- 25. Гершон Р.К., Ротрок Н., Ханрахан Р., Басс М., Селла Д. Использование PROMIS и центра оценки для предоставления показателей результатов, сообщаемых пациентами, в клинических исследованиях. Журнал прикладных измерений. 2010; 11 (3): 304. pmid: 20847477
- 26. Хердман М., Гудекс С., Ллойд А., Янссен М.Ф., Кинд П., Паркин Д. и др. Разработка и предварительное тестирование новой пятиуровневой версии EQ-5D (EQ-5D-5L). Исследование качества жизни. 1 декабря 2011 г.; 20 (10): 1727–36. pmid: 21479777
- 27.Доступно по адресу: https://www.economicsnetwork.ac.uk/health/EQ_5D_index_calculator.xls Цитировано 21 марта 2018 г.
- 28. Доступно по адресу: https://www.census.gov/2010census/ Цитировано 21 марта 2018 г.
- 29. Доступно по адресу: https://www.cdc.gov/nchs/nhis/nhis_2016_data_release.htm Цитировано 21 марта 2018 г.
- 30. Ханмер Дж., Лоуренс В. Ф., Андерсон Дж. П., Каплан Р. М., Фрайбек Д. Г.. Отчет о национальных репрезентативных значениях для неинституционализированного взрослого населения США для 7 показателей качества жизни, связанных со здоровьем.Принятие медицинских решений. Июль 2006 г.; 26 (4): 391–400. pmid: 16855127
- 31. Fryback DG, Dunham NC, Palta M, Hanmer J, Buechner J, Cherepanov D, et al. Нормы США для шести общих показателей качества жизни, связанных со здоровьем, из исследования National Health Measurement. Медицинская помощь. 2007 декабрь; 45 (12): 1162. pmid: 18007166
- 32. Ханмер Дж., Хейс Р.Д., Фрайбек Д.Г. Способ применения важен для национальных оценок качества жизни, связанного со здоровьем, в США. Медицинская помощь. 1 декабря 2007 г.; 45 (12): 1171–9.pmid: 18007167
- 33. Макдауэлл I. Измерение здоровья : Руководство по оценочным шкалам и анкетам . Издательство Оксфордского университета, США. 2006)
- 34. Каплан Р.М., Талли С., Хейс Р.Д., Фини Д., Ганиатс Т.Г., Палта М. и др. Пять основанных на предпочтениях индексов у пациентов с катарактой и сердечной недостаточностью не одинаково реагировали на изменения. Журнал клинической эпидемиологии. 2011 1 мая; 64 (5): 497–506. pmid: 20685077
- 35. Фини Д., Спритцер К., Хайс Р.Д., Лю Х., Ганиатс Т.Г., Каплан Р.М. и др.Соглашение об идентификации пациентов, которые меняются со временем: осторожные результаты у пациентов с катарактой и сердечной недостаточностью. Принятие медицинских решений. 2012 Март; 32 (2): 273–86. pmid: 22009666
- 36. Ханмер Дж., Каплан РМ. Обновление отчета о национальных репрезентативных ценностях для неинституционализированного взрослого населения США для пяти показателей качества жизни, связанных со здоровьем. Ценность в здоровье. 2016 31 декабря; 19 (8): 1059–62. pmid: 27987633
- 37. Лю Х., Селла Д., Гершон Р., Шен Дж., Моралес Л.С., Райли В. и др.Репрезентативность интернет-панели информационной системы измерения исходов, сообщаемых пациентами. Журнал клинической эпидемиологии. 30 ноября 2010 г .; 63 (11): 1169–78. pmid: 20688473
Строки детализации заказа на скоринг
Укажите метод оценки, который система использует для определения оценки заказа для обработки выполнения. Значения:
Пусто: используйте основной метод подсчета очков.
1: Используйте расширенный метод подсчета очков.
Примечание. Система вычисляет балл для расширенной оценки по формуле: Оценка = [(Приоритет типа заказа × Взвешенный процент типа заказа) + (Приоритет типа строки × Взвешенный процент типа строки) + (Запрошенная дата Возрастной приоритет × Запрошенная дата Взвешенный процент ) + (Приоритет клиента × Взвешенный процент клиента) + (Приоритет пользовательской бизнес-функции × Пользовательский взвешенный процентный показатель)]
Укажите процентное значение, которое система использует для расчетного веса расширенного предпочтения Приоритет типа заказа.
При использовании расширенного метода оценки система умножает это процентное значение на значение, полученное из расширенного предпочтения Приоритет типа заказа (42), и включает результат при вычислении взвешенной оценки.
Система обрабатывает введенное вами значение в процентах.Вы должны ввести значение от 0 до 100 включительно. Сумма взвешенных вариантов обработки должна равняться 100.
Укажите процентное значение, которое система использует для расчетного веса расширенного предпочтения «Приоритет типа линии».
При использовании расширенного метода оценки система умножает это процентное значение на значение, полученное из расширенного предпочтения «Приоритет типа линии» (43), и включает результат при вычислении взвешенной оценки.
Система обрабатывает введенное вами значение в процентах. Вы должны ввести значение от 0 до 100 включительно. Сумма взвешенных вариантов обработки должна равняться 100.
Укажите процентное значение, которое система использует для расчетного веса клиента, проданного приоритету.
При использовании метода расширенной оценки система умножает это процентное значение на числовое значение кода специальной обработки, которое она извлекает из приоритета «Продано клиенту» (UDC h50 | PR), и результат включается в расчет взвешенной оценки.
Система обрабатывает введенное вами значение в процентах. Вы должны ввести значение от 0 до 100 включительно. Сумма взвешенных вариантов обработки должна равняться 100.
Укажите процентное значение, которое система использует для расчетного веса расширенного предпочтения Запрошенный приоритет даты.
При использовании расширенного метода оценки система умножает это процентное значение на значение, полученное из расширенного предпочтения Запрошенный приоритет даты (44), и включает результат при вычислении взвешенной оценки.
Система обрабатывает введенное вами значение в процентах. Вы должны ввести значение от 0 до 100 включительно. Кроме того, сумма взвешенных вариантов обработки должна равняться 100.
Укажите процентное значение, которое система использует для расчетного веса пользовательской бизнес-функции.
При использовании расширенного метода оценки система умножает это процентное значение на числовое значение, которое она извлекает из функции расчета настраиваемого приоритета, определенной в следующем варианте обработки, и включает результат в расчет взвешенной оценки.
Система обрабатывает введенное вами значение в процентах. Вы должны ввести значение от 0 до 100 включительно. Сумма взвешенных вариантов обработки должна равняться 100.
Укажите имя бизнес-функции, которое система использует для расчета настраиваемого приоритета, используемого для определения оценки строки. Функция расчета настраиваемого приоритета использует предопределенную структуру данных D4277701A и возвращает числовой приоритет через параметр оценки порядка.
Для основного метода оценки система использует пользовательский приоритет в качестве критерия для получения оценки из таблицы настройки базовой оценки выполнения. Если вы оставите этот параметр обработки пустым, система получит ноль в качестве значения оценки для пользовательской функции.
Для расширенного метода оценки система умножает значение приоритета, полученное из пользовательской функции, на весовой коэффициент для пользовательского приоритета и включает результат в суммирование оценки.Если вы оставите этот параметр обработки пустым, система извлечет ноль в качестве значения для включения в суммирование баллов.
Укажите предпочтительное расписание, которое система будет использовать вместо предпочтительного расписания по умолчанию, определенного в системных константах. Это расписание управляет обработкой предпочтений для дополнительных предпочтений Приоритет типа заказа (42), Приоритет типа строки (43) и Приоритет запрошенной даты (44), которые используются при расчете расширенного метода оценки.
Примечание. Для изменения расписаний предпочтений используйте программу «Расширенные настройки расписания» (P4070) в меню «Дополнительные настройки» (G40311).
При использовании основного метода оценки укажите, будет ли система устанавливать предупреждение, когда система не находит базовую оценку. Система использует ноль в качестве значения по умолчанию для оценки в строке заказа.
Если высокий балл указывает на более важный приоритет, вам не нужно настраивать базовые данные скоринга для строк заказа с самым низким приоритетом.
Если низкая оценка указывает на более важный приоритет, ноль может быть действительной оценкой для строк деталей заказа. Используйте эту опцию обработки, чтобы система выдавала предупреждение, когда счет для строки заказа не может быть найден. Этот параметр предотвращает случайное присвоение строкам наиболее важной оценки приоритета.
Значения:
Пусто: не устанавливать предупреждение.
1: Установить предупреждение.
Правила подсчета очков по дихотомическим предпочтениям
Автор
Abstract
В этой статье мы изучаем индивидуальные стимулы для правдивого сообщения о предпочтениях для особого случая, когда индивидуумы имеют дихотомические предпочтения по набору альтернатив, а предпочтения агрегированы в форме правил подсчета баллов.В частности, мы показываем, что (а) подсчет Борды совпадает с голосованием за одобрение в области дихотомических предпочтений, (b) подсчет Борды является единственным доказывающим стратегию правилом подсчета баллов в области дихотомических предпочтений, и (c) если не менее трех люди участвуют в выборах, то дихотомическая область предпочтений является единственной областью максимального богатства, в которой граф Борда является стратегически обоснованным.
(Этот реферат был заимствован из другой версии этого документа.)
Предлагаемое цитирование
DOI: 10.1007 / s00355-007-0270-z
Скачать полный текст от издателя
Поскольку доступ к этому документу ограничен, вы можете поискать другую версию ниже или найти другую версию.
Другие версии этого продукта:
Ссылки на IDEAS
- Berga, Dolors & Serizawa, Shigehiro, 2000.« Максимальный домен для правил, доказывающих стратегию, с одним общественным благом », Журнал экономической теории, Elsevier, vol. 90 (1), страницы 39-61, январь.
- Богомольная, Анна и Мулен, Эрве и Стонг, Ричард, 2005. « Коллективный выбор при дихотомических предпочтениях ,» Журнал экономической теории, Elsevier, vol. 122 (2), страницы 165-184, июнь.
- Barbera, Salvador & Sonnenschein, Hugo & Zhou, Lin, 1991. « Голосование комитетов ,» Econometrica, Econometric Society, vol.59 (3), страницы 595-609, май.
- Майкл Даммит, 1998. « Подсчет Борды и манипуляции с повесткой дня », Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, т. 15 (2), страницы 289-296.
- Дэвид А. Смит, 1999. « Меры манипулирования общими функциями социального выбора «, Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, т. 16 (4), страницы 639-661.
- Чинг, Стивен и Серизава, Шигехиро, 1998.« Максимальный домен для существования правил, доказывающих стратегию », Журнал экономической теории, Elsevier, vol. 78 (1), страницы 157-166, январь.
- Мартин Барби и Клеменс Пуппе и Аттила Таснади, 2006 г. « Неуправляемые домены для счета Борда ,» Экономическая теория, Springer; Общество по продвижению экономической теории (SAET), т. 27 (2), страницы 411-430, январь.
- Саари, Дональд Дж., 1990. « Восприимчивость к манипуляциям ,» Общественный выбор, Springer, т.64 (1), страницы 21-41, январь.
Цитаты
Цитаты извлекаются проектом CitEc, подпишитесь на его RSS-канал для этого элемента.
Цитируется по:
- Кентаро Хацуми, Долорс Берга и Шигехиро Серизава, 2014. « Максимальный домен для правил, доказывающих стратегию и не требующих вето, в модели выбора нескольких объектов », Международный журнал теории игр, Springer; Game Theory Society, т.43 (1), страницы 153-168, февраль.
- Марк Форсац, 2007. « Утверждающее голосование по дихотомическим предпочтениям », Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, т. 28 (1), страницы 127-141, январь.
- Федерика Серон и Стефан Гонсалес, 2019. « Характеристика голосования за утверждение без допущения голосования за утверждение», Рабочие бумаги halshs-02440615, HAL.
- Франсуа Манике и Филипп Монген, 2015.« Утверждающее голосование и теорема о невозможности Эрроу », Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, т. 44 (3), страницы 519-532, март.
- Дарманн, Андреас и Кламлер, Кристиан и Пферши, Ульрих, 2009 г. « Максимизация минимального удовлетворения избирателя на связующих деревьях », Математические социальные науки, Elsevier, vol. 58 (2), страницы 238-250, сентябрь.
- Нинджбат Ууганбаатар, 2012 г. « Замечания к теореме Юнга «, Бюллетень экономики, AccessEcon, vol.32 (1), страницы 706-714.
Самые популярные товары
Это элементы, которые чаще всего цитируют те же работы, что и эта, и цитируются в тех же работах, что и эта.- Кентаро Хацуми, Долорс Берга и Шигехиро Серизава, 2014 г. « Максимальный домен для правил, доказывающих стратегию и не требующих вето, в модели выбора нескольких объектов », Международный журнал теории игр, Springer; Game Theory Society, т. 43 (1), страницы 153-168, февраль.
- Аки Лехтинен, 2007.« Правило Борда также предназначено для нечестных людей. », Общественный выбор, Springer, т. 133 (1), страницы 73-90, октябрь.
- М. Санвер, 2009. « Стратегическая стойкость правила множественности в ограниченных доменах ,» Экономическая теория, Springer; Общество по продвижению экономической теории (SAET), т. 39 (3), страницы 461-471, июнь.
- Массо, Хорди и Неме, Алехандро, 2001. « Максимальный домен предпочтений в задаче деления », Игры и экономическое поведение, Elsevier, vol.37 (2), страницы 367-387, ноябрь.
- Чаттерджи, Шуроджит и Санвер, Ремзи и Сен, Арунава, 2013. « На доменах, которые допускают правильное поведение функций социального выбора, защищающих от стратегии ,» Журнал экономической теории, Elsevier, vol. 148 (3), страницы 1050-1073.
- Ребело С., 1997. « На детерминанте экономического роста «, Рабочие документы RCER 443, Университет Рочестера — Центр экономических исследований (RCER).
- Жорди Массо, электронная почта автора: jordi.masso@uab.es и Алехандро Неме, 2002 г. « Максимальный домен предпочтений для правил только для вершин в задаче деления », Рабочие документы UFAE и IAE 535.02, Unitat de Fonaments de l’Anàlisi Econòmica (UAB) и Institut d’Anàlisi Econòmica (CSIC).
- Krzysztof Kontek & Honorata Sosnowska, 2020. « Особые вкусы или клики присяжных? Как снизить уровень манипуляции при принятии решений группой? », Групповое решение и переговоры, Springer, vol. 29 (6), страницы 1057-1084, декабрь.
- Элерс, Ларс, 2002. « Коалиционное выделение жилья для подтверждения стратегии «, Журнал экономической теории, Elsevier, vol. 105 (2), страницы 298-317, август.
- Берга, Долорс и Сэридзава, Сигехиро, 2000. « Максимальный домен для правил, доказывающих стратегию, с одним общественным благом », Журнал экономической теории, Elsevier, vol. 90 (1), страницы 39-61, январь.
- Паоло Джованни Пиаквадио, 2017. « Справедливое оправдание утилитаризма «, Econometrica, Econometric Society, vol.85, страницы 1261-1276, июль.
- Пико, Джереми и Сен, Арунава, 2012 г. « Крайняя точка характеристики случайных функций социального выбора, защищенных от стратегии: случай с двумя альтернативами ,» Economics Letters, Elsevier, vol. 115 (1), страницы 49-52.
- Томоя Казумура и Шигехиро Сэридзава, 2016 г. « Эффективность и стойкость к стратегии в задачах назначения объектов с множественными предпочтениями », Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, т.47 (3), страницы 633-663, октябрь.
- Erdamar, Bora & Sanver, M. Remzi & Sato, Shin, 2017. « Оценка устойчивости стратегии ,» Игры и экономическое поведение, Elsevier, vol. 106 (C), страницы 227-238.
- Alcalde-Unzu, Jorge & Vorsatz, Marc, 2018. « Стратегическое расположение объектов общественного пользования , г.» Игры и экономическое поведение, Elsevier, vol. 112 (C), страницы 21-48.
- Аррибильяга, Р. Пабло и Массо, Хорди, 2016. « Сравнение обобщенных схем медианного числа избирателей в соответствии с их манипуляциями «, Теоретическая экономика, Эконометрическое общество, т.11 (2) мая.
- Хидеюки Мизобути и Сигехиро Сэридзава, 2006 г. « Максимальный домен для стратегически обоснованных правил в экономике распределения », Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, т. 27 (1), страницы 195-210, август.
- Аки Лехтинен, 2007. « Последствия стратегического голосования для благосостояния в двух обычно используемых парламентских повестках дня «, Теория и решение, Springer, т. 63 (1), страницы 1-40, август.
- Green-Armytage, Джеймс, 2011.« Стратегическое голосование и выдвижение », Бумага MPRA 32200, Университетская библиотека Мюнхена, Германия.
- Хосе Алькантуд и Ритксар Арлеги, 2012 г. « Аксиоматический анализ наборов ранжирования при простой категоризации «, SERIEs: журнал Испанской экономической ассоциации, Springer; Испанская экономическая ассоциация, т. 3 (1), страницы 227-245, март.
Подробнее об этом продукте
Классификация JEL:
- D71 — Микроэкономика — — Анализ коллективного принятия решений — — — Социальный выбор; Клубы; Комитеты; Ассоциации
Статистика
Доступ и загрузка статистикиИсправления
Все материалы на этом сайте предоставлены соответствующими издателями и авторами.Вы можете помочь исправить ошибки и упущения. При запросе исправления укажите идентификатор этого элемента: RePEc: spr: sochwe: v: 31: y: 2008: i: 1: p: 151-162 . См. Общую информацию о том, как исправить материал в RePEc.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, заголовка, аннотации, библиографической информации или информации для загрузки, обращайтесь:. Общие контактные данные провайдера: http://www.springer.com .
Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь.Это позволяет привязать ваш профиль к этому элементу. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которых мы не уверены.
Если CitEc распознал библиографическую ссылку, но не связал с ней элемент в RePEc, вы можете помочь с этой формой .
Если вам известно об отсутствующих элементах, цитирующих этот элемент, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылочного элемента. Если вы являетесь зарегистрированным автором этого элемента, вы также можете проверить вкладку «Цитаты» в своем профиле RePEc Author Service, поскольку там могут быть некоторые цитаты, ожидающие подтверждения.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, названия, аннотации, библиографической информации или информации для загрузки, обращайтесь: Sonal Shukla или Springer Nature Abstracting and Indexing (адрес электронной почты указан ниже). Общие контактные данные провайдера: http://www.springer.com .
Обратите внимание, что исправления могут занять пару недель, чтобы отфильтровать различные сервисы RePEc.
Прогнозирование баллов по индексу SF-6D на основе предпочтений из опроса о состоянии здоровья SF-8 на JSTOR
АбстрактныйЦель Разработать и протестировать функции для прогнозирования оценок индекса SF-6D на основе предпочтений из обследования состояния здоровья SF-8.Методы. Это исследование было вторичным анализом данных, собранных в ходе обследования состояния здоровья населения, в котором респонденты (n = 7 529) заполнили анкеты SF-36 и SF-8. Мы исследовали семь обычных оценщиков наименьших квадратов на предмет их эффективности в прогнозировании оценок SF-6D из SF-8 как на индивидуальном, так и на групповом уровнях. Результаты В целом, все функции выполнялись одинаково хорошо при прогнозировании оценок SF-6D, и прогнозы на групповом уровне были лучше, чем прогнозы на индивидуальном уровне.На индивидуальном уровне 42,5–51,5% ошибок прогнозирования были меньше минимально важной разницы (MID) оценок SF-6D, в зависимости от характеристик функции, в то время как почти все ошибки прогнозирования тестируемых функций были меньше, чем MID для SF-6D на групповом уровне. Как на индивидуальном, так и на групповом уровне, тестируемые функции дали более низкие, чем фактические результаты, на верхнем конце шкалы SF-6D. Выводы В нашем исследовании были разработаны функции для генерации оценок индекса SF-6D на основе предпочтений на основе первого в своем роде обследования состояния здоровья SF-8.Необходимы дальнейшие исследования для оценки производительности и достоверности функций прогнозирования.
Информация о журналеQuality of Life Research — международный междисциплинарный журнал, посвященный быстрой публикации оригинальных исследований, теоретических статей и методологических отчетов, относящихся к области качества жизни во всех науках о здоровье. Журнал также публикует передовые статьи, литературу, обзоры книг и программного обеспечения, переписку и тезисы конференций.
Информация об издателеSpringer — одна из ведущих международных научных издательских компаний, издающая более 1200 журналов и более 3000 новых книг ежегодно, охватывающих широкий круг предметов, включая биомедицину и науки о жизни, клиническую медицину, физика, инженерия, математика, компьютерные науки и экономика.
.
