15 интересных логических задачек для детей и взрослых

Логические игры и головоломки — это отличное развлечение как для детей, так и для взрослых. Они вырабатывают привычку думать, рассуждать, делать выводы и всегда стараться найти решение проблемы.

Задачка про волка, козу и капусту

Помните старинную задачу про волка, козу и капусту? Кто не решал ее в детстве! Предложите задачу своему ребенку! Мужику нужно перевезти через реку волка, козу и капусту. Но в лодке может поместиться только он сам, а с ним или только волк, или только коза, или только капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как мужику перевезти свой груз?

Решение:

Нужно начать с козы. Перевезя ее, мужик возвращается на другой берег и берет волка. Переправив волка, он оставляет его на другом берегу, но зато берет козу и везет ее обратно на первый берег. Здесь он оставляет ее и перевозит к волку капусту. Затем, вернувшись, берет козу — переправа благополучно заканчивается.

Детективная задачка

На лугу лежат пять кусочков угля, одна морковь и шарф. Никто не клал их туда. Почему они там лежат?

Решение:

Дети использовали эти предметы, когда лепили снеговика зимой. С приходом весны снеговик растаял, и пять кусочков угля, морковка и шарф остались лежать уже на лугу.

Летная задачка

Мужчина выпрыгивает без парашюта из самолета. Высадка небезопасная, но мужчина остается целым и невредимым. Почему?

Решение:

Самолет находится ещё на взлётно-посадочной полосе.

Задачка про ноги

Ваня идет к лесному озеру. Ему навстречу движется класс из 25 учеников и двух преподавателей. Родители 10 детей также принимают участие в прогулке. Пять матерей еще везут своих детей на колясках. Преподаватель ведет с собой собаку. Сколько ног идут по дороге к лесному озеру?

Решение:

По дороге к лесному озеру идут только две ноги — Ванины. Все, кого он встретил, возвращаются с озера.

Сколько ворон?

Вишня у Маши плодоносит в большом количестве. К сожалению, на дерево садятся вороны и безжалостно клюют плоды. Вечером Маша считает ворон. Их 38! Это настолько выводит ее из себя, что она ловит одну ворону сачком. Сколько ворон осталось на дереве?

Решение:

Осталась только одна ворона, пойманная Машей. Остальные вороны испугались и улетели.

Задачка на внимательность

Молодая девушка заказывает в кафе яблочный сок, рулет и шоколадное мороженое. Официант, который принимает заказ, приносит ей вскоре все желаемое. После того как девушка оплатила заказ, официант спросил: «Трудно работать в полиции?» Как он догадался, что девушка — полицейский?

Решение:

Девушка была в полицейской форме.

День рождения князя

Когда князь празднует день рождения, его подданные должны принести ему достойный подарок: самую сочную ветчину, самый пряный сыр, самую упитанную курицу, искусно выделанные шкурки, плетеные корзинки, глиняные кувшины и резные изделия. Крестьянин сделал князю необычный подарок: бутылку с яблочным соком. Отличие этого подарка — яблоко находится в бутылке. Князь поражен: каким образом тот смог засунуть яблоко в бутылку? «Как ты сделал это? При помощи колдовства?» — спрашивает князь. Крестьянин отвечает: «Догадайтесь сами, но я вовсе не чародей!» Как яблоко попадает в бутылку?

Решение:

Крестьянин надевает бутылку на яблоневую ветку вскоре после цветения. Таким образом, плод развивается в бутылке.

Еще один вид логических игр придется всем по вкусу — это игры с палочками. Для игры понадобится набор счетных палочек или любые палочки одинаковой длины и толщины (например, спички, с которых предварительно счистили серу), подойдут и полоски картона. Если вы играете вместе с детьми, то можно давать устные задания. Если ребенок играет один, подготовьте карточки с рисунком и условием игровой задачи.

Задание № 1

Переложи одну палочку так, чтобы дом смотрел в другую сторону.

Задание № 2

Переложи 3 палочки так, чтобы корова оглянулась и подняла хвост.

Еще несколько заданий с палочками из пособия С. И. Волковой «Математика и конструирование» (1−4 классы):

А в завершении мы хотим предложить вам самостоятельно изготовить знаменитую китайскую головоломку «Танграм». И в этом нам опять поможет пособие С. И. Волковой «Математика и конструирование».

Из деталей этой головоломки можно складывать разные фигуры. Сложите для начала 1 и 2 фигуры. Рисунок вам поможет. Теперь попробуйте сложить фигуры 3, 4, 5, 6. И с этим справились? Поздравляем!

Надеемся, что выполняя предложенные задания, вы и ваш ребенок не раз испытали радость от приложенных интеллектуальных усилий, а главное — от самостоятельно найденного решения.

Фото: NadyaEugene/masterone/Shutterstock.com, архив пресс-службы,

образованиеполезные советышколаобществоразвитие

Головоломка | Фермер, Коза, Волк и Капуста

Фермер хочет пересечь реку, но он не один. У него также есть коза, волк и капуста вместе с ним. Доступна только одна лодка, которая может поддерживать фермера, а также козла, волка или капусту. Таким образом, одновременно в лодке может быть только два объекта (фермер и еще один).
Но проблема в том, что если козу и волка оставить наедине (либо в лодке, либо на берегу), волк съест козу. Точно так же, если Козу и капусту оставить в покое, то коза съест капусту. Фермер хочет пересечь реку со всеми тремя своими пожитками: козой, волком и капустой.
Какую стратегию он должен использовать для этого?

Решение 1: Если взять волка на другую сторону, козел и капуста останутся вместе. Также удаление капусты оставит волка и козу наедине. Следовательно, фермер сначала возьмет козу с другой стороны и вернется один. У нас есть фермер, волк и капуста с одной стороны и коза с другой стороны.
Сейчас он возьмет с собой волка, бросит волка на другую сторону и вернется с козой. Итак, теперь с одной стороны у нас есть фермер, капуста и коза, а с другой стороны — волк.
Теперь он берет с собой капусту и возвращается один. Итак, теперь сценарий: фермер, коза с одной стороны и волк, капуста с другой стороны.
Теперь, наконец, он пересекает реку с козой и, таким образом, ему удается забрать с собой все свое имущество.

Ссылка: https://www.bhavinionline.com/2013/10/river-crossing-puzzle-farmer-wants-to-cross-with-wolf-goat-and-cabbage/

Решение 2: Эту задачу можно решить с помощью теории графов.
Рассмотрим 2 состояния: начальное (A) и конечное (B).
Изначально на правом берегу реки ничего нет, а на левом — коза, капуста и волк. И в конечном состоянии все трое (коза, капуста и волк) будут с правой стороны. Как мы можем перейти в состояние B из состояния A? На правом берегу могут быть такие комбинации козы (G), капусты (C), волка (W).
-> 0, G, W, C, GW , GC , WC, GWC
0 представляет начальное состояние (A), а GWC представляет конечное состояние (B). Мы можем смоделировать эту проблему как неориентированный взвешенный граф.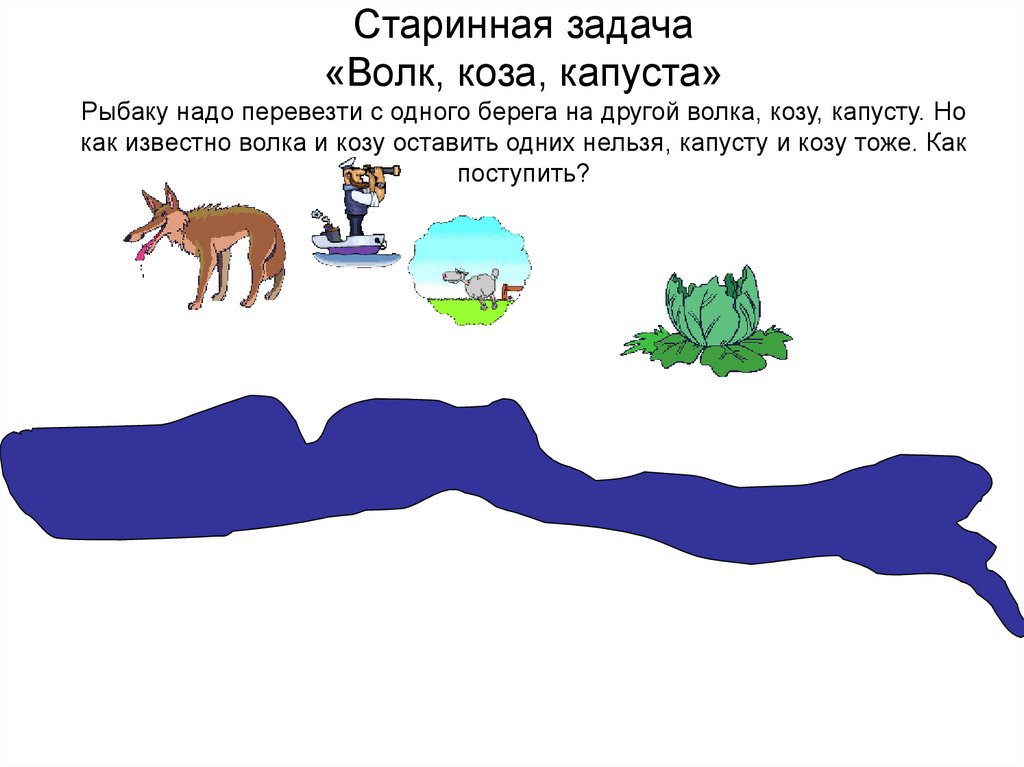 Где каждое ребро в графе имеет вес 1 или бесконечность.

Этот график можно использовать для представления нашей задачи.

Теперь все пути с бесконечным весом нельзя пройти, иначе ограничения задачи будут нарушены. Итак, мы должны двигаться от A к B, используя пути с весом 1, и мы можем найти допустимый путь, используя алгоритм кратчайшего пути Дейкстры.

Объяснение :
Понятно, что вначале лодочник может взять с собой только козу. Итак, от вершины 0 до вершины G мы устанавливаем вес равным 1. В других случаях (от 0 до W, от 0 до C) кого-то съедят. Следовательно, мы устанавливаем эти веса бесконечными.
Используя подобную интуицию, легко найти решение.

Эта статья предоставлена ​​ Arushi Dhamija. . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.

Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.

Пролог — Фермер, Коза, Волк, Капуста

Версия 1

На основе этой версии от UCSD.

%% Путь E -> W путешествие (е, ж). %% Путешествие W -> E путешествие (ш, д). %% Возможные ходы. двигаться([X,X,Коза,Капуста],волк,[Y,Y,Коза,Капуста]) :- путешествовать(X,Y). двигаться([X,Волк,X,Капуста],коза,[Y,Волк,Y,Капуста]):- путешествовать(X,Y). двигаться([X,Волк,Коза,X],капуста,[Y,Волк,Коза,Y]) :- путешествовать(X,Y). двигаться([X,Волк,Коза,Капуста],ничего,[Y,Волк,Коза,Капуста]) :- путешествовать(X,Y). %% Безопасные условия. безопасный([X,_,X,_]). % Коза находится на том же берегу, что и фермер. безопасно([X,X,_,X]). % Волк и капуста находятся на том же берегу, что и фермер решить([е,е,е,е],[]). решить (состояние, [FirstMove|OtherMoves]): — переместить (состояние, FirstMove, NextState), безопасно (NextState), решить (NextState, OtherMoves).

Версия 2 Дополнения

not_member(_, []) :- !. not_member(X, [Голова|Хвост]): – Х \= Голова, не_член(Х, Хвост). решить2(AnsPath):- решить2([[w,w,w,w]], AnsPath). решить2([S|_], [S]):- S = [e,e,e,e], !. решить2([S|Путь], [S|ПутьОтвета]) :- переместить(S, _, СледующееСостояние), безопасно(СледующееСостояние), not_member(NextState,[S|Path]), решить2([NextState, S | Path], AnsPath). % ?- решить2(X). % X = [[w, w, w, w], [e, w, e, w], [w, w, e, w], [e, e, e, w], [w, e, w , ш], [е, е, ш, е], [ш, е, ю, е], [е, е, е, е]] ; % X = [[w, w, w, w], [e, w, e, w], [w, w, e, w], [e, e, e, w], [w, e, w , ш], [е, е, ш, е], [ш, е, ю, е], [е, е, е, е]] ; % X = [[w, w, w, w], [e, w, e, w], [w, w, e, w], [e, w, e, e], [w, w, w , e], [e, e, w, e], [w, e, w, e], [e, e, e, e]] ; % X = [[w, w, w, w], [e, w, e, w], [w, w, e, w], [e, w, e, e], [w, w, w , e], [e, e, w, e], [w, e, w, e], [e, e, e, e]] ;