Комбинации в домино: Домино - подробные правила игры

Стратегии и хитрости игры в домино Козел

Домино Козел — самая известная разновидность развлечения, в которое так любили играть мужчины среднего возраста во времена Советского Союза. Однако с появлением интернета домино не исчезло, наоборот, теперь в него с интересом играют онлайн все, включая школьников и представительниц слабого пола.

Игра в домино онлайн решает многие вопросы:

• не надо искать партнеров для развлечения;
• играть можно в любое время, хоть в 2 часа ночи;
• не нужно заботиться о покупке набора для игры.

Чем же так привлекательно домино Козел по сравнению с другими разновидностями? Его правила очень простые, но по темпераментности игра даст фору многим другим развлечениям. Однако существуют маленькие хитрости, которые помогут вам побеждать в этой забаве.

Секреты игры в домино Козел

А сейчас более конкретно о небольших секретах игры в домино Козел.

• В ситуации, когда у вас после раздачи сложился расклад с относительно равномерным распределением точек на пластинках (имеется ввиду, 1:3, 2:4, 3:5, 0:3, 1:2 и т. д. — на любой заход вам будет, чем ответить), необходимо ходить так, чтобы у вас сохранялось как можно большее количество пластин с разными числами. Т.е. стараться “поддерживать ассортимент”. Напоминаем, что существует по 7 пластинок с каждым числовым значением (1:1, 1:2, 1:3, 1:4, 1:5, 1:6, 1:0 и т.д.)
• Если же у вас на руках, в основном, пластинки с одинаковым количеством точек на половинках (1:6, 1:5, 1:4, 1:1 и т.д), следует постараться заставить соперника пропускать ходы. Т.е. делать все возможное, чтобы цепочка с обеих сторон заканчивалась одинаковыми числовыми значениями. Возможно, вам и самому придется несколько раз пропустить ход, но это будет во благо.
• Обычно от дублей лучше всего избавляться как можно скорее.
• Если уже вышли 5 пластин с одинаковым значением, например, 6, и у вас находится 6-я пластинка, при этом дубль на руках у соперников, вам следует положить как можно скорее свою пластину. В таком случае дубль однозначно останется на руках противника.
• Как показывает практика, в около 60-70-и процентов случаев, если противник кладет фишку в другой конец ряда относительно своего предыдущего хода, то у него просто нет фишки с таким значением. Эту мелочь также можно использовать в своих интересах.
• Если у вас есть возможность положить пластинки с обеих сторон ряда, лучше выбрать ту, на которой больше точек, например, 6:5 — ведь в случае проигрыша вы запишете меньше очков на свой счет.
• Если в одном конце цепочки лежит пластинка, которая заканчивается, например, на 5, и последняя фишка с аналогичным значением находится у вас, то лучше придержать ее максимально дольше и таким образом запереть для соперников одно направление цепочки. Кладите ее только в крайнем случае.

Преимущества игры на нашем сайте

Эти нехитрые советы могут помочь вам стать победителем в домино Козел. Вы можете испробовать их на деле прямо сейчас, не теряя времени. Наш сайт отлично подойдет для этого. Играть можно бесплатно и без регистрации, в удобное время.

Есть возможность сыграть с живыми людьми, как с незнакомцами, так и с друзьями — просто договоритесь с ними зайти на сайт в одно время. Вы можете настроить игру для себя — выбрать количество участников и фон стола, определить количество необходимого на ход времени.

И помните, в наши дни в играть не только интересно, но и модно!

ПРОБНАЯ ИГРА
без регистрации

Фокус с запоминанием последовательности 28 костяшек домино

Домино — что мы о нем знаем? Немного знаем о его происхождении (Древний Китай), что название игры имеет связь с названием плаща у монахов, который с одной стороны был черным, а с другой — белым. Также каждый слышал об эффекте домино, когда одно событие или явление влечет за собой серию подобных.

Сегодня мы расскажем вам об удивительном человеке, который умеет запоминать последовательности из костяшек домино. Такие люди, обладающие феноменальной памятью, называются мнемотехниками. Природа наградила их способностью запоминать огромные количества цифр, различные комбинации из домино и карт и т. д.

В 2017-м году в рамках проекта “Удивительные люди”, в котором участвуют люди, обладающие самыми разными талантами, выступил мнемотехник, запомнивший последовательность из 28-ми костяшек, т.е. полного комплекта домино.

Как все происходило

Участнику телевизионного шоу давалось 2 минуты, чтобы запомнить порядок фишек, при этом на столе были выложены 2 одинаковые последовательности. Мужчине завязали глаза, после чего одну последовательность перевернули, чтобы затем по ней сверить правильность расклада мнемотехника. Второй ряд фишек тщательно перемешали.

Казалось бы, как можно запомнить огромное количество точек, где 2, где 5, что находилось вверху и что внизу? Но эта задача невыполнима только для обычного человека, не для специалиста, который имеет талант и вдобавок постоянно тренируется.

Когда мнемотехнику развязали глаза, он с легкостью выполнил задание.

А ларчик просто открывался. Разгадка фокуса

Однако, как оказалось, задание совершенно не имело смысла для мнемотехника. На самом деле фишки были расставлены совсем не беспорядочно. Первыми шли те, чьи точки в сумме дают десять: 5:5 и 6:4. Затем со значением восемь: 4:4, 5:3 и 6:2. Затем — 6, потом 4 и 2. Это были четные цифры. Вторая часть выстроенного ряда была с нечетной суммой точек на пластинках: 11-9-7-5-3-1.

Мы не знаем достоверно, были ли фишки разложены именно в таком порядке специально, чтобы облегчить задачу участнику. Этой информацией владеют только авторы проекта. Но после обнаружения такой закономерности задание очень упростилось: необходимо было только запомнить расположение точек внутри каждого маленького “отсека.” При желании, наверное, любой человек сможет развлечь гостей на вечеринке подобным фокусом.

Игра в домино на сайте domino-game.com

На нашем сайте каждый желающий может в домино играть бесплатно. Более того, регистрация совсем не обязательна, хотя возможна. Если вы захотите потратить всего одну минуту, а то и меньше, на регистрацию, будете вознаграждены дополнительными бонусами.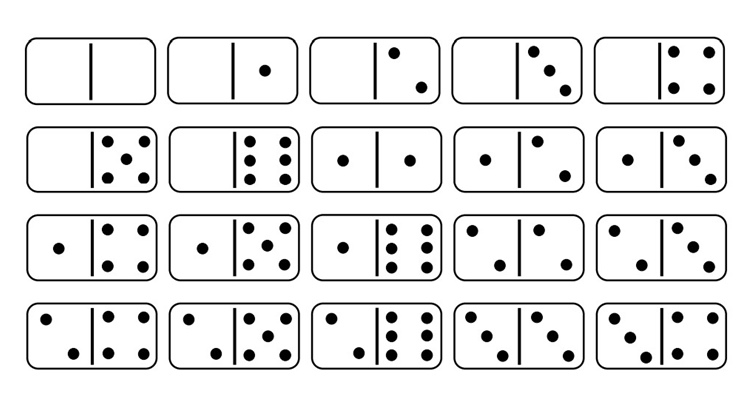

Приглашайте играть своих друзей или играйте с незнакомцами — ведь мы даем возможность играть с живыми людьми. Просто оставьте заявку на игру, и партнер найдет вас в кратчайшее время.

Если вы захотите освежить правила игры в домино Козел, например, прочитайте их перед началом процесса. Инструкции к каждой разновидности домино написаны на нашем сайте очень доступным языком.

ПРОБНАЯ ИГРА
без регистрации

математических комбинаций домино

математическая комбинаций домино

наборы для игры в домино

—

Домино стоит в ряду других игровых конструкций и имеет атрибуты присуща любым игровым системам, но это гораздо больший игровой замысел, а не другие, такие как шахматы или игральные карты или шашки, потому что количество домино может быть организовано очень разнообразно. А именно соотношение шахматных фигур с поля шахматной доски в классических шахматах оптимальны, если не учитывать Японские или китайские варианты этой древней игры, а также цвета (масти) и численные значения классических игральных карт оптимальны, но коэффициент игры элементы (фишки или плитки) и цифровые системы домино с квадратами шахматные доски могут иметь вариации, а исследование различных математических костяшек домино комбинации является выдающейся загадкой.

Традиционное домино представляет собой полные наборы фигур, которые выглядят как прямоугольные жетоны или плитки, или по-другому сказать игральные карты или кубики с числа, образующие парные числовые комбинации, обозначенные точками.
Количество костяшек в комплектах исчисляется всей возможной парой или иным образом сказать двукратные комбинации чисел или цифр от 0 до N. Полные наборы наиболее известны домино с комбинациями цифр от 0 до 6 или от 0 до 9, но гипотетически цифровые интервалы могут быть от 0 до бесконечности. Более того, некоторые комбинации цифр в комплектах могут повторяться или отсутствовать, а также колоды домино могут быть распределены по цифровым пропорциональным группам.
По математическим системам комбинаций домино в разных полных наборы позволяют различать шахматные доски на различных рядах клеток, и, таким образом, размеры игрового пространства могут быть разнообразными.
Именно в упаковке этой настольной игры есть оптимальная шахматная доска, на которой 8 вертикальных и 8 горизонтальных рядов, что аналогично классической шахматной доске, и комплекты домино, организованные таким образом, чтобы играть на 64 полях.

Но кроме того, математическая система домино позволяет рассчитывать разные соотношения цифровых жетонов с конфигурациями различных игровых досок.
Варианты математических комбинаций домино и цифровых систем показаны на Таблица.

Строки таблицы показывают интервалы домино комбинации от 0 до N. Правые столбцы показывают количество костяшек в наборах, соответствующих до строк, а также количество дублей и дробей. А также количества костяшек в комплектах с повторяющимися дублями или дроби, а именно количество числовых комбинаций домино в случае что двойные числа или дроби будут представлены дважды. Например, полный набор с комбинациями цифр от 0 до 9 включает 55 домино из 10 двойных и 45 дробей. Если полный комплект включает дважды удвоение, то содержит 65 токенов, а если дважды дроби затем содержит 100 частей домино. Третий комплект домино в упаковке настоящего настольная игра на страницах этого сайта соответствует третьей строке и четвертый столбец в показанной таблице, а именно две колоды по 16 элементов с удвоенные доли цифровых комбинаций от 0 до 3. И главное полное наборы не соответствуют числовым значениям показанной таблицы, т.к. в их дизайне есть только несколько повторяющихся двойников. На самом деле показанная таблица является элементарной схемой математического домино. комбинации, но номера в наборах и цифровых системах домино могут быть организованы в более сложных конструкциях.

В таблице показаны только общие числовые комбинации и цифровые системы в соответствии с которым можно изменить количество номеров в комплектациях и дизайнерские конструкции домино, но на самом деле изменения могут быть очень другой. Подробное исследование различных математических систем домино я постараюсь публиковать в будущем на страницах этого сайта.

—

Комплект домино традиционный или классический с цифровым интервал от 0 до 6 включает 28 токенов. Такая математическая система домино чисел требует шахматную доску с 8 горизонтальными и 7 вертикальными рядами квадраты, как 7×8 = 56/2 = 0,28.
На самом деле размеры игрового пространства зависят от правил конкретной игры или головоломок, но конфигурации игровых досок должны соответствовать системам количества в комплектах, а именно должны быть пропорциональны расположению домино на квадратах с учетом математики.
Дизайн традиционной или иначе сказать классической комплектации домино в пределах пропорциональной шахматной доски показано на рисунке:

Жетоны домино распределены по пропорциональные игровые группы, расположенные на противоположных половинах схематическая доска в виде шахматных фигур. 14 жетонов каждой пропорциональной группы полностью расставляют квадраты из двух крайние горизонтали, что подобно расположению фигур в шахматы, и, следовательно, 7 вертикалей и 8 горизонталей подходят для это цифровая система домино. Или можно применить шахматная доска, имеющая 7 вертикалей и 7 горизонталей. Стрелки справа показывают, как следует ставить обозначения фокусировки жетоны двух пропорциональных групп, то есть фактически показанная картинка является технический чертеж домино, по которому можно сделать этот вариант настольной игры. 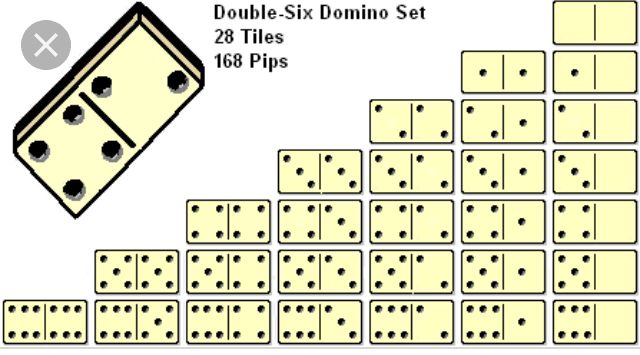Цифры за платой схемы показывают сумму цифр по вертикали и горизонтальные ряды, соответствующие магическому квадрату, образующие цифровые система в классической комплектации домино в показанной игре позиций, потому что суммы по каждой вертикали 24, а по каждой горизонтали 21, или 21+21=42. Информацию о магических квадратах и нумерологии чисел смотрите на страницах другого сайта: www.numeralgame.64g.ru.

Надо сказать, что показанный магический квадрат домино не вырастают из расчетов анонимных математиков или неизвестных ученых, как телепередачи рассказали по телевизору на одном из телеканалов. Но тот или иной возможные магические квадраты являются конструктивными частями изобретения, что подтверждается патент RU2259223, в соответствии с которым организован дизайн настоящей настольной игры.
А также надо сказать, что показанная традиционная комплектация 28 жетоны домино и игровое поле из 7 вертикалей и 8 горизонталей можно взять за модель для игр в программе чемпионатов мира по международным Федерация домино. Как такая математическая система цифрового домино комбинации классические.

—

Полный набор костяшек с комбинациями чисел от 0 до 7 и удвоенное количество фракций.
Цифровая система такой колоды соответствует шахматной доске из 8 вертикалей и 8 горизонталей, так как содержит 64 жетона домино, которые соответствуют 64 квадратам, что точно соответствует классической шахматной доске.
Игровая конструкция или иначе сказать числовое оформление данного комплекта выглядит так, как показано на картинке.

Темные и светлые треугольники обозначают жетоны из двух пропорциональные группы. А также треугольники — это обозначения фокусировки, согласно которому домино должно быть ориентировано на шахматную доску. Двойники обозначаются разнонаправленными треугольниками как их ориентация значения не имеет, но треугольники разных направлений темные и свет, что обозначает принадлежность двойников к пропорциональным группам. Жетоны домино двух пропорциональных групп тоже обозначаются контрастные треугольники на спине. Математические комбинации домино данного комплекта могут иметь интервал от 1 до 8 вместо от 0 до 7 и знаки цифровой системы будут соответствовать числовым обозначениям вертикалей и горизонталей шахматная доска. Тогда можно играть в игры и головоломки в правила которого основаны на соотношениях костяшек домино с числовыми значениями квадратов. Правила и инструкции таких игр в домино не описаны в руководство в файлах PDF, а также изображения данного комплекта для печати не представлены. Но необходимые фото могу дать на почту если кто-то желает распечатать этот вариант игры и попробовать игровой процесс. Этот вариант игрового дизайна тоже можно рассматривать как цифровую модель для чемпионаты мира и турниры под эгидой Международного Федерация домино. В виде математической системы из 64 жетонов домино соответствует классической шахматной доске, позволяющей играть полностью открытая информация и равные шансы игроков на победу как в шахматы, что является необходимым критерием спортивных игр. В результате игры с домино можно признать видом спорта, а можно отнести Международным олимпийским комитетом в программах олимпиад как официальная спортивная дисциплина.

Из этого комплекта можно убрать жетоны с номером 7. затем математическая система цифровых комбинаций включает 49 домино и подходов для шахматной доски, имеющей 7 вертикальных и 7 горизонтальных рядов. Но распространение на пропорциональные группы в данном случае учитывать нельзя, так как уменьшенная колода содержит не четное количество домино.
Либо можно убрать жетоны с номерами 7 и 6. Математическая система цифровых комбинаций в данном случае содержит 36 костяшек домино и подходит для шахматная доска, имеющая 6 вертикалей и 6 горизонталей. Распределение на пропорциональное группы при этом правильно, а именно можно считать темными и светлыми треугольники во время игр или головоломок.
Подобным образом математические системы цифр в этом комплекте костяшек домино может быть уменьшено еще больше, и в результате последовательного удаления токенов с числа 7, 6, 5, 4, 3 будут иметь количественные изменения в зависимости от размеров шахматные доски, имеющие 7х7, 6х6, 5х5, 4х4, 3х3 ряда. По сути, это математическое система комбинаций домино обладает уникальным цифровым свойством согласно которым различные интервалы чисел соответствуют шахматным доскам одинакового вертикали и горизонтали, или иначе сказать с равномощными числовыми квадраты. Это можно учитывать в правилах различных головоломок и головоломок с домино.

Цифровая матрица домино.

Числа нанесены на жетоны домино или игральные карты Показанная комплектация необычным способом, а именно шестнадцатеричным цифровым используется матричная вместо десятичной. Эта матрица позволяет обозначать числа от 0 до 15 с помощью точек. А именно очки домино могут иметь 16 числовых значений, причем очень большое благодаря ему могут быть организованы комплекты или конструкции игровых конструкций. На рисунке показаны некоторые варианты, в соответствии с которыми положения точек в матрицу обозначают цифрами, но обозначения могут отличаться от предложенных, а именно дизайн домино может быть разным.

Дизайн данной игровой упаковки может состоять из разных комплектаций и колод Всего домино.
Комплекты с большими интервалами номеров могут содержать мелкие цифровые интервалы, так что меньшие колоды могут быть получены при сокращении больших, и каждая При этом система цифр может быть распределена на пропорциональные игровые группы. А именно некоторые комплекты могут быть объединены в один, и каждый может быть распределен на пропорциональные группы, или иначе сказать цифровую систему домино одного общий комплект может включать в себя математические комбинации чисел домино которые сгруппированы по числовым соотношениям разного порядка.
Таким образом, дизайн жетонов домино может иметь соответствующие обозначения, которые игроки можно было выбрать разные комплектации и пропорциональные группы разных заказы, а также мог различать свое и чужое домино.
Дополнительно дизайн жетонов или игральных карт может иметь ориентировочные обозначения которые соответствуют распределению пропорциональных групп и позволяют иметь домино на клетках шахматной доски в игровых позициях как фигуры в шахматная игра, обеспечивающая равные шансы игроков на получение приза.
Многие возможные варианты домино могут быть детально рассчитаны и подготовлены для промышленное производство, если производители настольных игр или книгоиздательские фирмы, или частные издатели будут заинтересованы в коммерческом применении любой игровой конструкции, которые описаны на страницах этого сайта.
Гипотетически эту интеллектуальную логическую игру можно рассматривать как набор конструктивные цифровые элементы, позволяющие формировать разнообразные комплекты или колоды домино и различных конфигураций игровых досок. Или самое простое полные наборы математических комбинаций домино могут быть подготовлены для промышленных изготовление настоящей настольной игры.

Все показанные конструктивные решения и цифровые системы домино являются подтвержденные патентами на изобретения, а также свидетельством об действующем модель RU 30332.

Детали показанных комплектов могут быть изготовлены не только из бумаги, так и напечатаны игральные карты, но и в виде плиток и жетонов из различных материалов, и в том числе из природных камней . В частности, с помощью мрамора и гранита, или различные полудрагоценные камни в качестве сувенирных и подарочных экземпляров.
Игровые доски тоже могут быть изготовлены из различных натуральных и полудрагоценных камней в формы игровых столов, которые могут быть интересны как необычными, так и неординарными подарками президентам издательских фирм и производителей игрушек , а также менеджерам промышленных компаний, которые могут осуществлять массовое производство и торговлю раздача показанных вариантов домино .

---

и выше

Математика домино

Давайте определим множество [n-n] домино, состоящее из всех возможных костяшек домино. между [0-0] и [n-n]. Традиционные западные наборы домино сет [6-6] или двойная шестерка, [9-9] или двойная девятка, и набор [12-12] или двойные двенадцать.

Хотя ясно, что двойная шестерка получена из игральных костей, я понятия не имею, с чего начались большие наборы. Эскимосы и У индейцев-инуитов Канады есть наборы домино из костей животных от 61 до 148 штук в наборе для азартных игр. я не знаю, если они местного происхождения или если они могли видеть западные домино и попытался их скопировать.

Размер набора

Количество костей в наборе из [n-n] костяшек определяется формула ((n ² + 3н + 2)/ 2). Например, количество плиток в наборе [18-18] равно (18*18 + 3*18 + 2)/2 = 190. 0-0] 1 [1-1] 3 [2-2] 6 [3-3]. [4-4] 15 [5-5] 21 [6-6] 28 <= most common set [7-7] 36 [8-8] 45 [9-9] 55 <= Коммерчески доступный набор [10-10] 66 [11-11] 78 [11-11] 780. -12] 91 <= серийно выпускаемый набор [13-13] 105 [14-14] 120 [15-15] 136 9009164 [15-15] 136 <= Коммерный. 16-16] 153 [17-17] 171 [18-18] 190 <= Коммерческий доступный1119 9014 190 <= Коммерчески доступный11114888888.

Одно из самых важных свойств набора [n-n] костяшек домино состоит в том, что любое число k (где 0 <= k <= n) появится (n+2) раз на плитках. Причина, по которой это важно для игрока, что когда вы хотите знать, можете ли вы заблокировать другого игрока, вы может быстро подсчитать количество вхождений числа в вашей руке и на Таблица. Если количество равно (n+2), вы знаете, что нет другой игрок может сопоставить это число. Ищите двойника, обычно играть спиннером в большинстве игр, и вы найдете четыре из восьми вхождений сразу.

Учитывая набор из [n-n] костей домино, можно ли расставить все плитки в один поезд? Поезд — это ряд плиток, каждая из которых концы совпадают с концом плитки слева от них и правильно, за исключением двух крайних плиток, которые совпадают только на одном конце, конечно.

Можете ли вы собрать набор в один круговой поезд? циркуляр поезд представляет собой кольцо из плиток, уложенных встык, где оба конца каждой плитка соответствует своим левым и правым соседям. Очевидно, если кольцевой поезд существует, его можно разорвать в любой момент, чтобы дать единый поезд.

Методом проб и ошибок ответ для нулевого набора — «да». для одного поезда, потому что это тривиальный поезд сам по себе. ответ «нет» для кольцевого поезда, потому что один член набор не может наклониться, чтобы коснуться самого себя.

Набор [1-1] состоит из плиток [0-0], [0-1] и [1-1]. который является поездом, если играть в таком порядке, но это не кольцевой поезд. По мере увеличения значения (n), отвечая на этот вопрос методом проб и ошибок будет намного сложнее.

Вместо этого давайте воспользуемся другим подходом; теория графов. В то время как я нет времени вдаваться в математику теории графов в подробно, я надеюсь, что смогу охватить достаточно, чтобы объяснить это решение.

Граф представляет собой структуру математического моделирования, состоящую из узлов (точки) и края (линии). Количество ребер, входящих и исходящих of node — это степень узла.

Давайте сделаем так, чтобы узлы представляли числа от 0 до (n) и ребра между ними будут плитки в [n-n] наборе домино. Двойной это показан в виде дуги, которая начинается и заканчивается в одном узле. Эти графы будут иметь столько ребер, сколько костяшек домино в наборе моделируют. Например, вот график для набора костяшек [2-2]:

Теперь мы можем преобразовать задачу поиска поезда в задача найти путь через граф набора домино, который касается всех краев. Проблема кругового поезда становится такой нахождения пути через граф набора домино, который включает все ребра и возвращается к узлу, из которого он начался. К счастью, это проблема теории графов, которая уже была решена. решен Леонардом Эйлером сотни лет назад и известен как «Мосты Кенигсбергской проблемы». Для такого кольцевого поезда существовать либо

1. Каждый узел имеет четную степень или
2. Должно быть два и только два узла с нечетным ребром.

Таким образом, набор [3-3] нельзя поместить в один поезд потому что его узлы имеют степень 5. Набор «Двойная шестерка» можно положить в поезд, потому что его узлы имеют степень 8. Обратите внимание, что степень узлов графа набора домино [n-n] всегда будет (n+2), так что легко ответить на поезд и кольцевой поезд вопросы. Если (n) четно, то для этого существует круговой поезд. набор домино. Если (n) нечетно, то поездов (n+1)/2, каждый оканчивающийся цифрой между нулем и (n).

Обычный вопрос: сколько различных поездов можно построить из стандартного комплекта «двойная шестерка». Не занимаясь математикой, ответ будет 7 959 229 931 520, если вы считаете развороты, или половину этой суммы, если вы этого не делаете.

Закон Кларка

Это довольно интересный результат, который говорит о том, что в заблокированной игре в домино с одним спином сумма четырех ветвей таблицы всегда должна составлять четное число.

Первое следствие закона Кларка состоит в том, что сумма четырех рук в заблокированной игре всегда является четным числом. Это связано с тем, что набор двойной шестерки содержит 168 пунктов, что является четным числом, а четное число минус четное число является четным числом.

Второе следствие закона Кларка состоит в том, что сумма рук двух товариществ в заблокированной игре должна быть либо четной, либо нечетной.

Закон Кларка вытекает из того факта, что удвоения всегда четные, поэтому против спиннера будут четыре одинаковые половинки. Затем в каждом рукаве концы плиток должны быть спаренными, чтобы они были ровными, пока вы не дойдете до конца рукава. Если рука заканчивается дублем, то открытая плитка четная.

На столе можно сделать блок с двумя, тремя или четырьмя руками. Это еще больше сводит к четырем рукам с одним и тем же числом, что дает нам четный счет, или к четверкам с двумя мертвыми числами. Ситуация с тремя руками в заблокированной игре требует, чтобы все они заканчивались той же мастью, что и спиннер.

Домино и шахматные доски

«Изуродованная шахматная доска» — это классическая демонстрация метода расстановки наборов в определенном классе задач. Задача состоит в том, чтобы спросить, можете ли вы покрыть шахматную доску, противоположные углы которой были срезаны, костяшками домино, которые ровно покрывают две клетки шахматной доски.

Судя по осмотру, на изуродованной шахматной доске 64 — 2 = 62 клетки, поэтому нам понадобится 31 клетка, если предположить, что решение существует. Теперь посмотрите, как костяшка домино может сидеть на доске — она обращена лицом либо к северу-югу, либо к востоку-западу. Но независимо от того, как она ориентирована, плитка всегда покрывает одну черную и одну белую клетку. Изуродованная шахматная доска имеет 32 черных клетки и 30 белых клеток. Поэтому никогда нельзя покрывать доску.

Другие доказательства можно найти в литературе. Стэн Вагон опубликовал «Четырнадцать доказательств результата о мозаике прямоугольника», American Mathematical Monthly, 14, 94-1987, стр. 601-617.

Можно было бы ожидать, что если бы удаленные квадраты были разного цвета, то и ответ, и решение были бы совсем другими. Действительно, покройте всю шахматную доску костяшками домино. Вырежьте два квадрата из-под одной из частей. Оставшаяся часть доски по-прежнему будет покрыта оставшимися костяшками домино. Таким образом, по крайней мере, иногда оставшаяся доска «покрывается». В качестве разминки вы можете рассмотреть эту задачу:

Задача 1

Накройте две произвольные клетки шахматной доски костяшкой домино. Всегда ли можно закрыть оставшуюся часть доски большим количеством плиток, не нарушая первоначальную часть?

Теперь вы можете пойти дальше и ослабить одно из условий задачи 1: что, если квадраты не являются смежными? У нас уже есть решение, если они одного цвета. Тогда остается только один случай.

Задача 2

С шахматной доски удалены две произвольные клетки разного цвета. Можно ли закрыть оставшуюся часть доски костяшками домино так, чтобы каждая костяшка домино покрывала ровно две клетки?

Решение

Да, это всегда возможно. Чтобы увидеть это, нарисуйте две вилки, как показано красным на схеме.

Это разбивает шахматную доску на цепочку чередующихся квадратов. Достаточно немного поэкспериментировать, чтобы убедиться, что цепочку можно пройти, начав с любой клетки и покрывая сразу две клетки плиткой. Это наблюдение фактически решает проблему.

Какой следующий вопрос, связанный с покрытием шахматной доски домино? Мой сын Дэвид задал следующий вопрос:

Задача 3

Предположим, что на каждом шаге мы удаляем пару квадратов разного цвета. Какое максимальное количество пар можно удалить, чтобы оставшуюся часть доски всегда можно было закрыть костяшками домино?

An Aside

Это вполне законный вопрос, потому что очевидно, что в одном экстремальном случае, когда мы удаляем все, кроме двух несмежных квадратов, проблема покрытия того, что осталось, будет неразрешимой, по крайней мере, для некоторых конфигураций. С другой стороны, как мы только что видели, удалив всего два квадрата, мы получим разрешимую задачу. Тогда должно быть пограничное число где-то посередине.

Сначала проблема может показаться сложной. Но нужно с чего-то начинать. Как это часто бывает, экспериментирование с несколькими частными случаями помогает понять более общую проблему. Итак, давайте начнем со следующего простейшего случая удаления четырех квадратов (2 белых и 2 черных). Вилки, которые так хорошо работали в предыдущем случае, становятся бесполезными. Действительно, следуя по цепочке, мы можем удалить два последовательных белых и два последовательных черных квадрата. Это еще не доказывает, что полученная таким образом конфигурация неразрешима; но сомнения в том, что проблема может не иметь простого решения, могут начать закрадываться в ваш разум. В этот момент может иметь смысл подумать о возможности отрицательного результата. Можем ли мы придумать контрпример? Другими словами, возможно, можно оставить «незакрываемую» доску, просто удалив две пары клеток.

Что может сделать доску непокрытой? Вспоминая нашу первоначальную задачу, если бы можно было выделить область шахматной доски, содержащую нечетное количество клеток, мы могли бы утверждать, что решение задачи 3 равно 1, всего одной паре.

Решение

Можно удалить две пары квадратов, чтобы оставить шахматную доску, которую нельзя покрыть. Действительно, уберите два белых квадрата, примыкающих к черному углу. Это создает область, состоящую из одного (углового) квадрата, у которого нет соседних белых квадратов.

Задача 4

Предположим, что нам разрешено удалить 2 белых и 2 черных квадрата так, чтобы доска еще не развалилась, т. е. не раскололась на две или более отдельных частей. Всегда ли можно закрыть домино все, что осталось от доски?

Замечание

Пытаясь ответить на задачу 4, я столкнулся с одной непокрываемой конфигурацией, в которой удалены 3 пары квадратов. На схеме изображен правый нижний угол.

Квадраты с серым контуром обрезаны (3 черных квадрата — предполагается, что три белых квадрата были удалены в другом месте).